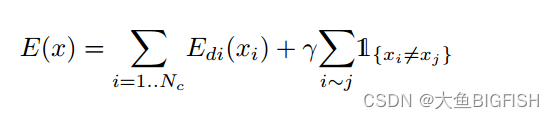建立机器人的动力学模型是完成力控的基础，常用的动力学模型建模法有拉格朗日法和牛顿-欧拉法，其中牛顿-欧拉采用递推形式，计算更为简便，使用也更为广泛。本文就来介绍下牛顿-欧拉的动力学建模方法，
PS，网上关于动力学建模的参考资料很多，看了一圈还是感觉《机器人学导论 Craig》写的最清楚，建议刚学习的时候还是看这种经典的书籍。下面的公式和图也都是来自《机器人学导论》，后续看书学习的时候也不会陌生。
我的知乎原文：机器人力控入门——牛顿欧拉法动力学建模 - 知乎
外推
理解牛顿-欧拉法建模有两个要点，其中一个是搞清楚连杆之间的速度/加速度传递关系（建立起 和
以及
和
的关系），这是后面求解连杆间力/力矩的基础。
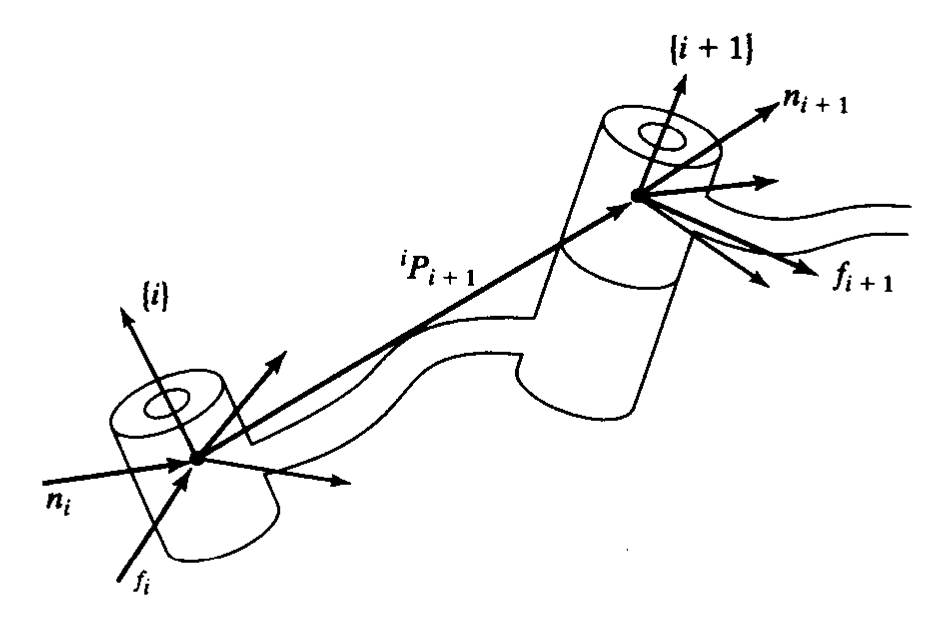
首先明确一下定义：和
这两个变量分别是连杆的线速度和角速度在坐标系
上表示，如图 1所示，
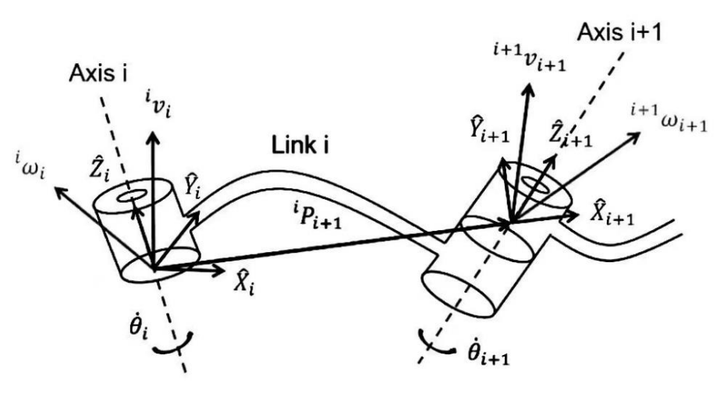
只有在同一个坐标系中，速度才能加减，也就是说，对于角速度和线速度
：
看一下公式（1），坐标系 i+1原点处的角速度除了自身的角速度，还包含上一个坐标系 原点处角速度的叠加。这里
表示关节角速度是沿着z轴方向的
公式（2）：坐标系 i+1原点处的线速度除了上一个坐标系 原点处的线速度，还包括由于坐标系 旋转带来的线速度。
这两个公式理解没有问题的话，下面的肯定也都能看懂。
对公式(1)和(2)求导，可得：
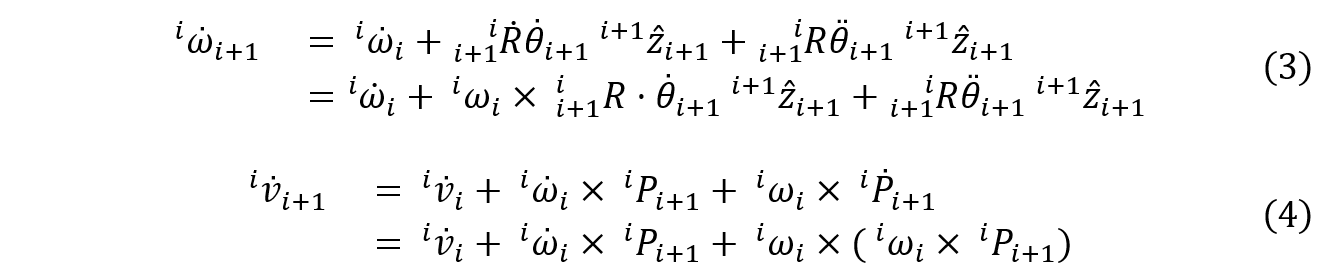
这个公式中可能会对这个部分有疑问：
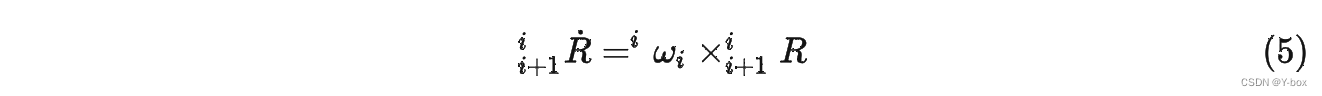
可以参考：旋转矩阵的导数（机器人学）_旋转矩阵求导_cuntou0906的博客-CSDN博客 或者以旋转矩阵的导数为关键词自行搜索。
同理，对原点处的线速度做平移，得到连杆 i质心处 的线速度，因为质心坐标系和连杆坐标系姿态相同，因此：
对(3)和(4)做坐标变换（乘以一个旋转矩阵），可以得到如下加速度传递关系:
内推
理解牛顿-欧拉法建模的另一个要点是要搞清楚连杆之间力/力矩的传递关系
同样的，先明确下力和力矩的定义，
如图 2所示， 表示由连杆 i-1作用在连杆 i上的力，
表示由连杆 i-1作用在连杆 i上的力矩。
连杆运动所需的力是关于加速度及其质量的函数，计算出每个连杆质心处的线加速度和角加速度之后，运用牛顿-欧拉公式，计算出作用在连杆质心 上的惯性力
和力矩
，由牛顿方程可得：
由欧拉方程可得：
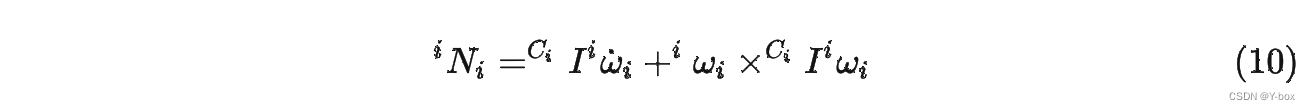
是连杆 的转动惯量，分析作用在连杆 上的力平衡关系：
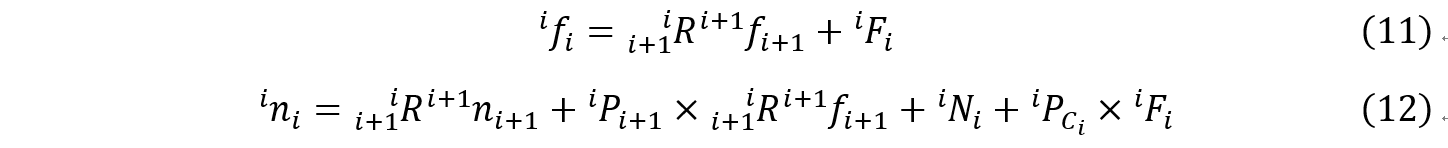
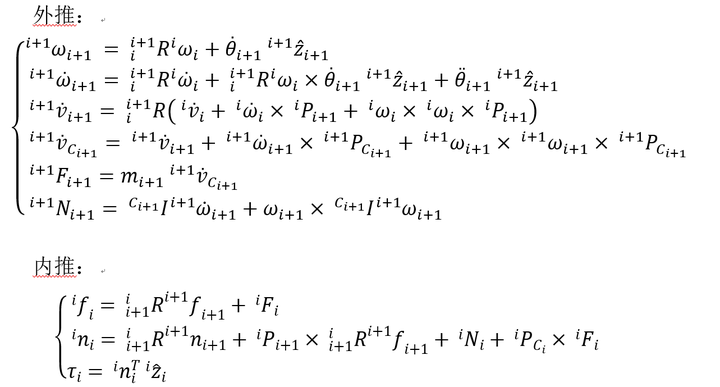
从内推和外推的公式中可以看出动力学模型中有一些变量时恒定不变的，如 
，这些参数被称为机器人的动力学参数，而后续在机器人平台上实现力控的下一个关键步骤就是要把这些变量辨识出来，这样就可以准确算出伺服系统要提供多大的转矩，从而实现机械臂（连杆）的运动控制。
如果把所有公式都带入到（13）式中展开，把它表示成 
的函数，那么就有了拉格朗日形式的动力学方程：
细心的朋友可能会发现这里面没有包含摩擦力矩，在上面牛顿-欧拉递推的过程中，确实是忽略了摩擦的，这可能是因为摩擦力本身模型不确定，单独加到关节上会更加简洁些。在辨识的时候会把摩擦力加上，或者单独辨识摩擦力。拉格朗日形式的动力学方程也会加上摩擦力矩，变成这样的形式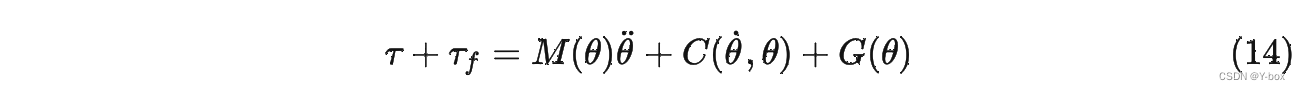
最后再贴一个学习资料sympybotics GitHub - cdsousa/SymPyBotics: [UNMAINTAINED] Symbolic Framework for Modeling and Identification of Robot Dynamics，这是一个用python的开源机器人运动学和动力学的符号推导工具包，可以去里面读读代码，看看人家是怎么实现的，这对理解机器人动力学会有很大帮助。（PS,这个工具包也是后面做辨识必不可少的，可以先阅读了解下）
