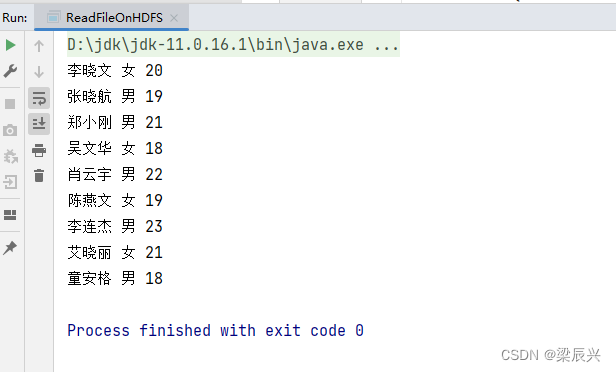
一、数据结构

 

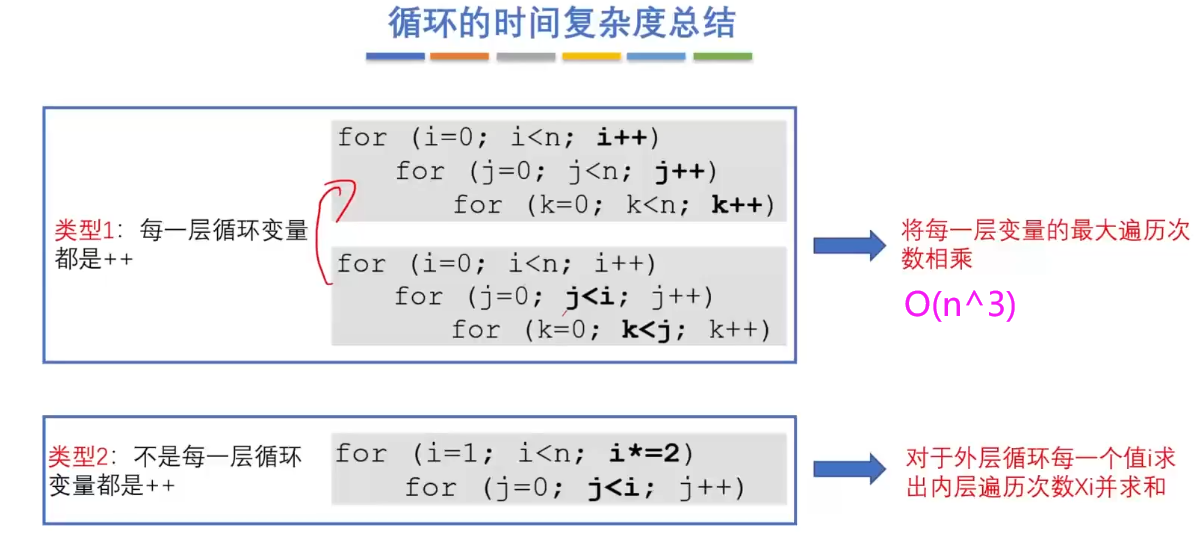
T1：时间复杂度 ——直接求程序执行的次数

        

 

T5：哈夫曼树（最优二叉树）与哈夫曼编码

• 定义
  • 结点带权路径长度：从根到任一节点的路径长度（经过的边数）与该结点权值的乘积
  • 树的带权路径长度WPL：所有叶节点的带权路径长度之和
  • 哈夫曼树：WPL最小的二叉树
• 哈夫曼树的构造与特点
  • 1、每个初始结点最终成为叶节点，权值越小的结点到根节点的路径长度越大
  • 2、构造过程中共构建了n-1个结点（双分支结点），因此哈夫曼树的结点总数为2n-1
  • 3、每次构造都选择两棵树作为新结点的孩子，因此不存在度为1的结点。
  • 用个叶子结点构造的哈夫曼树形态可能不唯一，但带权路径长度唯一。
  • 4、哈夫曼树结论:：WPL = 该树所有非叶结点的权值和
• 哈夫曼编码
  • 前缀编码
    • 如果没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码。