目录

逻辑回归原理

最大化似然函数和最小化损失函数

一、逻辑回归基本概念

1. 什么是逻辑回归

2. 逻辑回归的优缺点

3. 逻辑回归和多重线性回归的区别

Poisson分布

泊松分布的特点：

泊松分布用途

4. 逻辑回归用途

5. Regression 常规步骤

---

逻辑回归原理

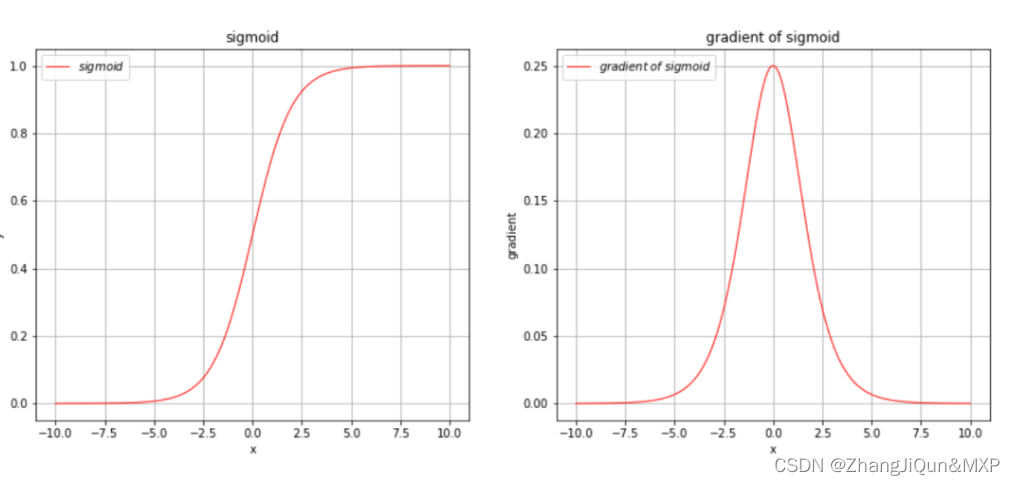
逻辑回归实际上是使用线性回归模型的预测值去逼近真实标记的对数函数。

逻辑回归虽然名字叫回归，但实际确实一种分类算法。其优点有：

• 直接对分类的可能性建模，无需实现假设数据分布，从而避免了假设分布不准确带来的问题（区别于生成式模型）；

• 不仅可预测出类别，还能得到该预测的概率，这对一些利用概率辅助决策的任务很有用；

• 对数函数是任意阶可导的凸函数，有很好的的数学性质，有许多数值优化算法都可以求出最优解。

最大化似然函数和最小化损失函数

经过一系列数学推导和证明，可知在逻辑回归模型中，最大化似然函数和最小化损失函数实际上是等价的，经典的数值优化算法，例如梯度下降和牛顿法，都可以求得其最优解。

一、逻辑回归基本概念

1. 什么是逻辑回归

逻辑回归就是这样的一个过程：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别）

回归模型中，y是一个定性变量，比如y=0或1，logistic方法主要应用于研究某些事件发生的概率

2. 逻辑回归的优缺点

优点：

1）速度快，适合二分类问题

2）简单易于理解，直接看到各个特征的权重

3）能容易地更新模型吸收新的数据

缺点：

对数据和场景的适应能力有局限性，不如决策树算法适应性那么强

3. 逻辑回归和多重线性回归的区别

Logistic回归与多重线性回归实际上有很多相同之处

最大的区别就在于它们的因变量不同，其他的基本都差不多。正是因为如此，这两种回归可以归于同一个家族，即广义线性模型（generalizedlinear model）。

这一家族中的模型形式基本上都差不多，不同的就是因变量不同。

如果是连续的，就是多重线性回归

如果是二项分布，就是Logistic回归

如果是Poisson分布，就是Poisson回归

如果是负二项分布，就是负二项回归

Poisson分布

是一种统计与概率学里常见到的离散概率分布，由法国数学家西莫恩·德尼·泊松（Siméon-Denis Poisson）在1838年时发表。

泊松分布的概率质量函数为：

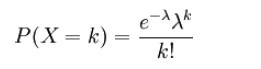
泊松分布表示（固定尺度的）连续区间（如时间，距离）上给定的事件发生次数的概率，所以可以看作泊松分布中n是无穷大的。二项分布是固定实验次数下，事件发生次数的概率，n是有界的。

泊松分布的特点：

泊松分布的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。

已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？有可能一下子出生6个，也有可能一个都不出生。这是我们没法知道的。

泊松分布用途

 

4. 逻辑回归用途

寻找危险因素：寻找某一疾病的危险因素等；

预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；

判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。

5. Regression 常规步骤

寻找h函数（即预测函数）

构造J函数（损失函数）

想办法使得J函数最小并求得回归参数（θ）