491.递增子序列

分析：存在重复元素，求递增子序列思路：1.树层去重2.当 i>0 时当前位大于上一位 

 

 思路：

• 去重逻辑在每一层都需要重新创建（每一层遍历），且不能影响到下一层递归

class Solution {
public:
    vector<vector<int>>res;
    vector<int>mid;
    
    void backtrace(vector<int>&nums,int startIndex){
        if(mid.size()>=2)
            res.push_back(mid);
        if(startIndex==nums.size())
            return;
        unordered_set<int>upset;//只影响该树层
        for(int i=startIndex;i<nums.size();i++){
            if(!mid.empty() && mid.back()>nums[i])//递增序列条件
                continue;
            if(upset.find(nums[i])!=upset.end())//该树层存在重复值，并且不是第一次遍历
                continue;
            upset.insert(nums[i]);//记录第一次遍历
            mid.push_back(nums[i]);
            backtrace(nums,i+1);
            mid.pop_back();
        }
    }
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        backtrace(nums,0);
        return res;
    }
};

46.全排列

思路一：直接在结果数组中查找是否出现过此下标

思路二：使用set进行下标去重

class Solution {
public:
    vector<vector<int>>res;
    vector<int>mid;
    unordered_set<int>index;
    void backtrace(vector<int>&nums,int start){
        if(start==nums.size()){
            res.push_back(mid);
            return;
        }

        for(int i=0;i<nums.size();i++){
            if(index.find(i)!=index.end())//在树枝中进行下标去重
                continue;
            index.insert(i);
            mid.push_back(nums[i]);
            backtrace(nums,start+1);
            mid.pop_back();
            index.erase(i);
        }
    }
    //树枝去重
    vector<vector<int>> permute(vector<int>& nums) {
        backtrace(nums,0);
        return res;
    }
};

47.全排列||

思路一：进行树枝的去重，树层的去重直接使用find函数

思路二：树层去重（需要排序）+树枝去重

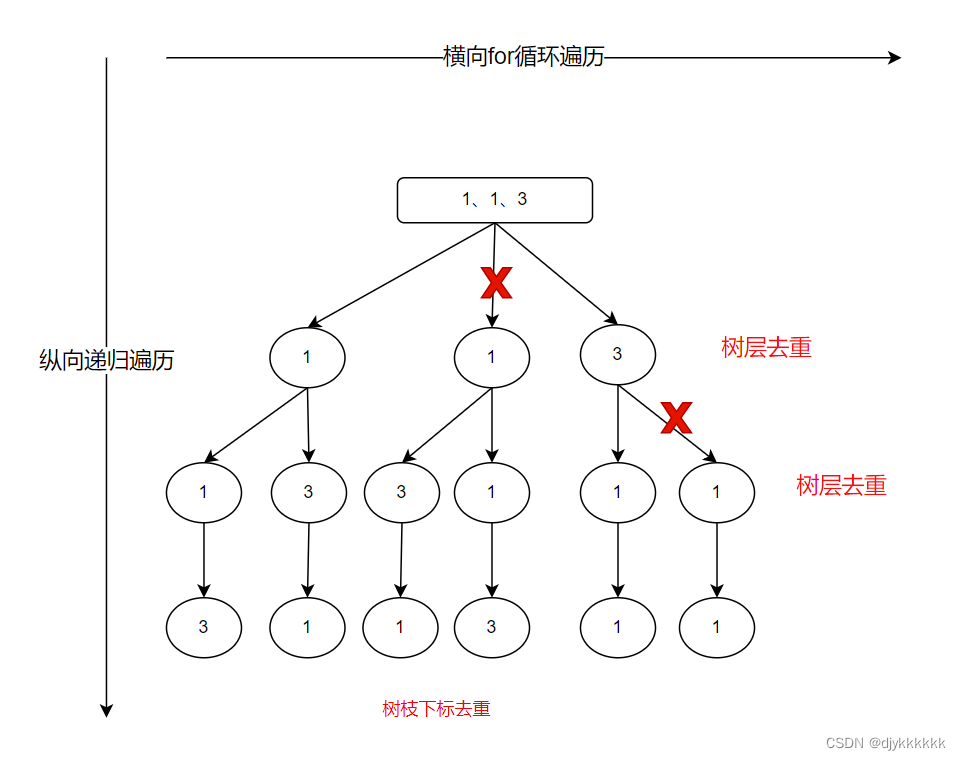
分析：本质上还是树层去重，在上一题全排列的基础上，每一层的遍历中有重复元素

class Solution {
public:
    vector<vector<int>>res;
    vector<int>mid;
    unordered_set<int>index;//记录递归下标
    
    void backtrace(vector<int>&nums,int start,vector<bool>&used){
        if(start==nums.size()){
            res.push_back(mid);
            return;
        }
        
        for(int i=0;i<nums.size();i++){
            if(i>0 && nums[i]==nums[i-1] && !used[i-1])//树层重复元素去重（used避免的树枝的去重，因为存在重复元素）
                continue;
            if(index.find(i)!=index.end())//树枝下标元素去重
                continue;
            index.insert(i);//树枝递归记录下标
            used[i]=true;//树枝递归记录使用
            mid.push_back(nums[i]);
            backtrace(nums,start+1,used);
            mid.pop_back();
            index.erase(i);
            used[i]=false;
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(),nums.end());//需要排序
        vector<bool>used(nums.size(),false);//记录重复值的使用
        backtrace(nums,0,used);
        return res;
    }
};

 455.分发饼干

思路：先排序，按最大的胃口和最大的饼干数来分配，使用双指针倒序遍历计数

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        int i=g.size()-1,j=s.size()-1;
        int sum=0,maxsum=0;
        while(i>=0 && j>=0){
            if(s[j]>=g[i]){
                j--;
                i--;
                sum++;
            }
            else
                i--;
            maxsum=max(maxsum,sum);
        }
        return maxsum;
    }
};

376.摆动序列

分析：考虑三种情况

• 存在单调增和单调减
• 存在平区间
• 在单调增或单调减中存在平区间

思路：遍历序列，采用三个变量，前数与当前数之差prediff，当前数与下一个数之差curdiff，摆动序列总长度sum。

当出现摆动时，即出现峰值：

• 单调区间直接判断prediff和curdiff一正一反；

• 平区间则判断prediff==0的情况下，若curdiff不为0则有摆动

• 出现峰值才更新preidff，不然在单调区间内存在平区间，就会导致每个平区间多一个记录

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        //思路一：直接计算峰顶和峰底的个数
        if(nums.size()<=1) return nums.size();
        int curDiff=0;//当前数和后一个数的差值
        int preDiff=0;//前一个数和当前数的差值（初始化为0方便第一个元素计算）
        int sum=1;
        for(int i=0;i<nums.size()-1;i++){
            curDiff=nums[i+1]-nums[i];
            //出现峰值的情况
            if((preDiff<=0 && curDiff>0) || (preDiff>=0 && curDiff<0)){
                sum++;
                preDiff=curDiff;//峰值出现后更新prediff
            }
        }
        return sum;
    }
};