渲染器（五）：快速diff算法

这章开始讨论第三种用于比较新旧vnode的方式：快速diff算法。跟它的名字一样，它很快。Vue3采用的就是这种算法，Vue2采用的是上一章中的双端diff算法。

接下来就来着重了解它的实现思路。

1.相同的前置元素和后置元素：

不同于简单diff算法和双端diff算法，快速Diff算法包含预处理步骤。这其实借鉴了纯文本diff算法的思路，即在对两段文本进行diff之前，先对它们进行全等比较：

if (text1 === text2) return;

如果全等，则无需进入核心diff算法。除此之外，预处理过程还会处理两段文本相同的前缀和后缀，如以下两段文本：

TEXT1: I use vue for app development 
TEXT2: I use react for app development

可以发现，除了第三个字符串vue 和 react不同，其它都一样。因此对于这两段文本，需要进行diff操作的部分是：TEXT1: vue ，TEXT2: react。这实际上是简化问题的一种方式。

这样子就能够轻松判断文本的插入和删除了。

例如插入操作，去除掉相同前缀内容后：

TEXT1: I like you
TEXT2: I like you too

TEXT1:
TEXT2: too

例如删除操作：

TEXT1: I like you too
TEXT2: I like you

TEXT1: too
TEXT2:

来看diff算法是如何做的，以下图中的新旧vnode为例：
在这里插入图片描述

它具有相同的前置节点p-1 和相同的后置节点 p-2 和p-3。对于相同的前置节点和后置节点，由于它们在新旧vnode中的相对位置不变，所以不需要移动，但仍然需要进行打补丁操作。

前置节点更新的处理：通过建立索引j，初始值为0，用来指向新旧vnode节点的开头，然后while循环向后遍历，让索引j自增，直到遇到拥有不同key值的节点为止。如图所示：
后置节点更新的处理：建立两个索引指向新旧vnode节点中的最后一个节点（因为新旧vnode子节点的数量可能不同，故需要两个索引），然后while循环从后向前遍历，直到遇到拥有不同key值的节点为止，如图所示：

实现代码如下：

function patchKeyedChildren(n1, n2, container) {
    // 处理前置节点
    const oldChildren = n1.children;
    const newChildren = n2.children;
    let j = 0;
    let oldVnode = oldChildren[j];
    let newVnode = newChildren[j];
    // while循环向后遍历,直到遇到拥有不同key值的节点为止
    while (oldVnode.key === newVnode.key) {
        patch(oldVnode, newVnode, container);
        j++;
        oldVnode = oldChildren[j];
        newVnode = newChildren[j];
    }

    // 处理后置节点
    let oldEnd = oldChildren.length - 1;
    let newEnd = newChildren.length - 1;
    oldVnode = oldChildren[oldEnd];
    newVnode = newChildren[newEnd];
    // while循环从后向前遍历,直到遇到拥有不同key值的节点为止
    while (oldVnode.key === newVnode.key) {
        patch(oldVnode, newVnode, container);
        oldEnd--;
        newEnd--;
        oldVnode = oldChildren[oldEnd];
        newVnode = newChildren[newEnd];
    }
}

在这一步更新操作过后，新旧vnode此时的状态如图所示：在这里插入图片描述

观察上图，可以发现还遗留了一个未被挂载的新增节点p-4。那么代码该怎么写呢？观察三个索引之间的关系：

条件一：oldEnd < j成立，说明在预处理过程中，所有旧vnode已处理完毕；
条件二：newEnd >= j成立，说明还有未被处理的新增节点。

两个条件成立，即说明需要执行挂载操作，并挂载到正确位置。就是说得把新增vnode挂载到节点 p-2所对应的真实DOM前面。所以节点p-2对应的真实DOM节点就是挂载操作的锚点元素。

代码实现：看新增加的if判断即可

function patchKeyedChildren(n1, n2, container) {
    // 处理前置节点
    const oldChildren = n1.children;
    const newChildren = n2.children;
    let j = 0;
    let oldVnode = oldChildren[j];
    let newVnode = newChildren[j];
    // while循环向后遍历,直到遇到拥有不同key值的节点为止
    while (oldVnode.key === newVnode.key) {
        patch(oldVnode, newVnode, container);
        j++;
        oldVnode = oldChildren[j];
        newVnode = newChildren[j];
    }

    // 处理后置节点
    let oldEnd = oldChildren.length - 1;
    let newEnd = newChildren.length - 1;
    oldVnode = oldChildren[oldEnd];
    newVnode = newChildren[newEnd];
    // while循环从后向前遍历,直到遇到拥有不同key值的节点为止
    while (oldVnode.key === newVnode.key) {
        patch(oldVnode, newVnode, container);
        oldEnd--;
        newEnd--;
        oldVnode = oldChildren[oldEnd];
        newVnode = newChildren[newEnd];
    }
    
    // 预处理完毕后,如果满足如下条件,说明还有未被挂载的新增节点
    if (j > oldEnd && j <= newEnd) {
        // 锚点索引
        const anchorIndex = newEnd + 1;
        // 锚点元素
        const anchor = anchorIndex < newChildren.length
            ? newChildren[anchorIndex].el : null;
        // 采用while循环,逐个挂载新增节点
        while (j <= newEnd) {
            patch(null, newChildren[j++], container, anchor);
        }
    }
}

代码解释都写在注释里了，接下来来看看删除节点的情况：

当新vnode的数量小于旧vnode时，就会出现需要删除节点的情况。举例：在这里插入图片描述

对相同的前置节点和后置节点进行预处理后，此时的状态如图所示：

在这里插入图片描述

索引j和索引oldEnd之间的任何节点都应该被卸载，具体实现如下：

    // 预处理完毕后,如果满足如下条件,说明还有未被挂载的新增节点
    if (j > oldEnd && j <= newEnd) {
        // 锚点索引
        const anchorIndex = newEnd + 1;
        // 锚点元素
        const anchor = anchorIndex < newChildren.length
            ? newChildren[anchorIndex].el : null;
        // 采用while循环,逐个挂载新增节点
        while (j <= newEnd) {
            patch(null, newChildren[j++], container, anchor);
        }
    } else if (j > newEnd && j <= oldEnd) {
        // 预处理完毕后,如果满足如下条件,说明还有未被卸载的旧节点
        while (j <= oldEnd) {
            unmount(oldChildren[j++]);
        }
    }

在前面代码上新增加的代码，多了一个 else...if 分支。解释都写在注释里啦。

2.判断是否需要进行DOM移动操作：

在上一节中，讲解了快速diff算法的预处理过程，即处理相同前置节点和后置节点。但是有时情况可能比较复杂，如下图：在这里插入图片描述

它只有少量的前置、后置节点，并且新vnode中多了p-7，少了p-6。

经过预处理后，无论是新旧vnode，都有部分节点未经处理，这时就需要进一步处理。

那么该怎么处理呢？其实无论是简单diff算法、双端diff算法，还是快速diff算法，它们都遵守同样的处理规则：

判断是否有节点需要移动，以及应该如何移动；
找出那些需要被添加或移除的节点。

那该怎么判断呢？其实在前面的基础上多添加一个else分支即可，因为三个索引都不满足下面两个条件中的任何一个：

j > oldEnd && j <= newEnd
j > newEnd && j <= oldEnd

具体处理思路：先构造一个source数组，它的长度等于新vnode在经过预处理后剩余未处理节点的数量，并且source中每个元素的初始值都是 -1 。
在这里插入图片描述

代码实现：看else分支即可

    // 预处理完毕后,如果满足如下条件,说明还有未被挂载的新增节点
    if (j > oldEnd && j <= newEnd) {
        // 锚点索引
        const anchorIndex = newEnd + 1;
        // 锚点元素
        const anchor = anchorIndex < newChildren.length
            ? newChildren[anchorIndex].el : null;
        // 采用while循环,逐个挂载新增节点
        while (j <= newEnd) {
            patch(null, newChildren[j++], container, anchor);
        }
    } else if (j > newEnd && j <= oldEnd) {
        // 预处理完毕后,如果满足如下条件,说明还有未被卸载的旧节点
        while (j <= oldEnd) {
            unmount(oldChildren[j++]);
        }
    } else {
        // 构造 source数组,保存新vnode中剩余未处理节点的数量
        const count = newEnd - j + 1;
        const source = new Array(count);
        source.fill(-1);
    }

数组source的作用：如上图所示，每个元素分别与新vnode中剩余未处理节点一一对应。

实际上，source 数组将用来存储新vnode在旧vnode中的位置索引，后面将使用它计算出一个最长递增子序列，并用于辅助完成DOM移动的操作。如下图展示了填充source数组的过程：在这里插入图片描述

介绍一下用双for循环的source数组填充实现：

else {
        // 构造 source数组,保存新vnode中剩余未处理节点的数量
        const count = newEnd - j + 1;
        const source = new Array(count);
        source.fill(-1);
		
		// 起始索引
        const oldStart = j;
        const newStart = j;
        // 遍历旧vnode
        for (let i = oldStart; i <= oldEnd; i++) {
            const oldVnode = oldChildren[i];
            // 遍历新vnode
            for (let k = newStart; k <= newEnd; k++) {
                const newVnode = newChildren[k];
                if (oldVnode.key === newVnode.key) {
                    patch(oldVnode, newVnode, container);
                    // 由于数组source的索引从开始,未处理节点的索引未必从0开始
                    // 所以填充时需要用 k - newStart来表示数组的索引值
                    source[k - newStart] = i;
                }
            }
        }
    }

用双for循环嵌套的时间复杂度有点高，可能会带来性能问题，所以需要进行优化。为新vnode构建一张索引表，用来存储节点key和节点位置索引之间的映射，如下图：
在这里插入图片描述

代码实现：

else {
        // 构造 source数组,保存新vnode中剩余未处理节点的数量
        const count = newEnd - j + 1;
        const source = new Array(count);
        source.fill(-1);

        // 起始索引
        const oldStart = j;
        const newStart = j;
        // 构建索引表
        const keyIndex = {};
        for (let i = newStart; i <= newEnd; i++) {
            keyIndex[newChildren[i].key] = i;
        }
        // 遍历旧vnode中剩余未处理的节点
        for (let i = oldStart; i <= oldEnd; i++) {
            oldVnode = oldChildren[i];
            // 通过索引表快速找到新vnode中具有相同key值的节点位置
            const k = keyIndex[oldVnode.key];
            if (typeof k !== 'undefined') {
                newVnode = newChildren[k];
                patch(oldVnode, newVnode, container);
                // 填充source数组
                source[k - newStart] = i;
            } else {
                // 没找到
                unmount(oldVnode);
            }
        }
    }

代码解释：

第一个for循环用来构建索引表，索引表：存储vnode的key值和在新vnode中位置索引的映射。
第二个for循环用来遍历旧vnode，并且用旧vnode中的key值去索引表中查找该节点在新vnode中具有相同key值的节点位置（因为新旧vnode的key相同）。存储到变量k中，如果k存在，说明该节点是可复用的，然后进行source数组填充。

source数组填充完了，接下来该思考如何判断节点是否需要移动？

通过新增两个变量moved和pos。前者初始值为false代表是否需要移动节点，后者初始值为0，代表遍历旧vnode的过程中遇到的最大索引值k。
在前面的简单diff算法时提到，如果在遍历过程中遇到的索引值呈递增趋势，说明不需要移动节点；反之需要。
所以在第二个for循环内通过比较变量k与变量pos的值来判断是否需要移动节点。

除此之外，还需要一个数量标识来代表已经更新过的节点数量。已经更新过的vnode数量应该小于新vnode中需要更新的节点数量。否则说明有多余节点，需要将其卸载。此时的代码：

else {
        // 构造 source数组,保存新vnode中剩余未处理节点的数量
        const count = newEnd - j + 1;
        const source = new Array(count);
        source.fill(-1);

        // 起始索引
        const oldStart = j;
        const newStart = j;
        // 新增两个变量moved和pos
        let moved = false;
        let pos = 0;
        // 构建索引表
        const keyIndex = {};
        for (let i = newStart; i <= newEnd; i++) {
            keyIndex[newChildren[i].key] = i;
        }
        // 新增 patched变量,代表更新过的节点数量
        let patched = 0;
        for (let i = oldStart; i <= oldEnd; i++) {
            oldVnode = oldChildren[i];
            // 如果更新过的vnode数量 小于 需要更新的vnode数量,则执行更新
            if (patched <= count) {
                const k = keyIndex[oldVnode.key];
                if (typeof k !== 'undefined') {
                    newVnode = newChildren[k];
                    patch(oldVnode, newVnode, container);
                    source[k - newStart] = i;
                    // 判断节点是否需要移动
                    if (k < pos) {
                        moved = true;
                    } else {
                        pos = k;
                    }
                } else {
                    // 没找到
                    unmount(oldVnode);
                }
            } else {
                // 如果更新过的vnode数量 大于 需要更新的vnode数量,则卸载多余节点
                unmount(oldVnode);
            }
        }
    }

3.如何移动元素？

如何判断是否需要进行DOM移动操作？

当moved值为true时，说明需要进行DOM移动操作

该如何移动元素？

source数组中保存着剩余未处理节点数量，里面存储着新vnode的节点在旧vnode中的位置。根据source数组计算出一个最长递增子序列，用于DOM移动操作。

啥是最长递增子序列？

假如给定序列中 [3,5,4,7]，那么它的最长递增子序列就是 [3,5,7]或者[3,4,7]。它的最长子序递增子序列可能有多个，需要注意的是后面它返回的结果是最长递增子序列中的元素在source数组中的位置索引。如上面例子中的 [0,1,3] 或 [0,2,3]

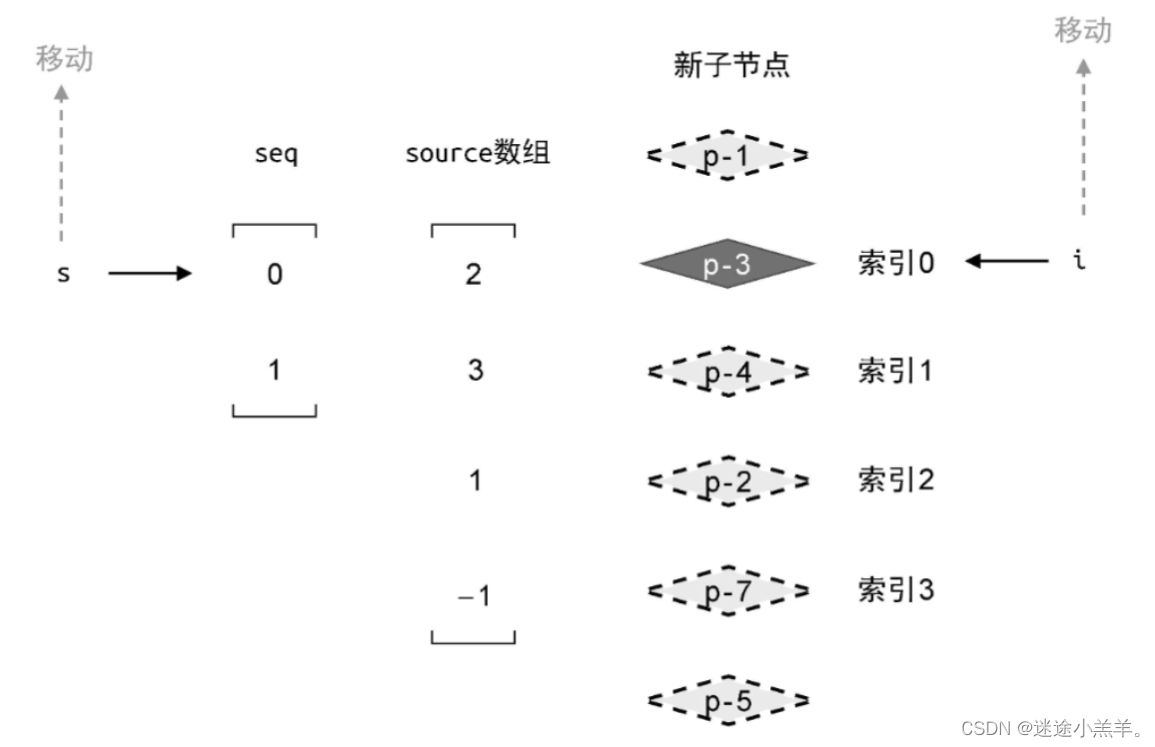
了解完上面的后，回归前面的例子，如图所示：
在这里插入图片描述

索引为0的节点是 p-2，索引为1的节点是 p-3，以此类推。重新编号是为了让子序列seq与新索引值产生对应关系。

以上例来说，子序列seq的值为 [0,1]，它的含义是：在新vnode中，重新编号后索引值为0和1的这两个节点在更新前后顺序没有变化。

即重新编号后，索引值为0和1的节点不需要移动。对应到新vnode就是节点p-3索引为0，节点p-4索引为1，所以节点p-3和p-4所对应的真实DOM不需要移动。就是说只有节点 p-2和p-7可能需要移动。

为了完成节点的移动，还需要创建两个索引值 i和s：

i指向新vnode中的最后一个节点；
s指向最长递增子序列中的最后一个元素。

接下来开启一个for循环，让变量i和s按照上图中箭头的方向移动，如下代码：

        if (moved) {
            // 计算最长递增子序列
            const seq = lis(source);
            let s = seq.length - 1;
            let i = count - 1;
            // for循环使得i递减，按照图中箭头的方向移动
            for (i; i >= 0; i--) {
                if (i !== seq[s]) {
                    // 符合条件则说明该节点需要移动
                } else {
                    // 当 i=== seq[s]时,说明该位置的节点不需要移动
                    s--;
                }
            }
        }

接下来就继续完善代码，执行更新。

第一轮循环：初始时索引i指向节点 p-7，由于节点p-7对应的source数组中相同位置的元素索引为-1，所以将p-7作为全新节点进行挂载。
第二轮循环：此时i=2，执行到下面代码中的第二步，i !== seq[s] 条件成立，节点p-2所对应的真实DOM需要移动。
第三、四轮循环：p-4，p-3不需要移动。

此时的代码：

        if (moved) {
            // 计算最长递增子序列
            const seq = lis(source);
            let s = seq.length - 1;
            let i = count - 1;
            // for循环使得i递减，按照图中箭头的方向移动
            for (i; i >= 0; i--) {
                // 说明索引为i的节点是全新节点,将其挂载
                if (source[i] === -1) {
                    // 该节点在新vnode中的真实位置索引
                    const pos = i + newStart;
                    const newVnode = newChildren[pos];
                    // 该节点的下一个节点的位置索引
                    const nextPos = pos + 1;
                    // 锚点
                    const anchor = nextPos < newChildren.length
                        ? newChildren[nextPos].el
                        : null;
                    // 挂载
                    patch(null, newVnode, container, anchor);
                } else if (i !== seq[s]) {
                    // 该节点需要移动
                    const pos = i + newStart;
                    const newVnode = newChildren[pos];
                    const nextPos = pos + 1;
                    const anchor = nextPos < newChildren.length
                        ? newChildren[nextPos].el : null;
                    insert(newVnode.el, container, anchor);
                } else {
                    // 该节点不需要移动,只需要让s指向下一个位置
                    s--;
                }
            }
        }

在这里插入图片描述

完整代码：

// 快速diff算法
function patchKeyedChildren(n1, n2, container) {
    // 处理前置节点
    const oldChildren = n1.children;
    const newChildren = n2.children;
    let j = 0;
    let oldVnode = oldChildren[j];
    let newVnode = newChildren[j];
    // while循环向后遍历,直到遇到拥有不同key值的节点为止
    while (oldVnode.key === newVnode.key) {
        patch(oldVnode, newVnode, container);
        j++;
        oldVnode = oldChildren[j];
        newVnode = newChildren[j];
    }

    // 处理后置节点
    let oldEnd = oldChildren.length - 1;
    let newEnd = newChildren.length - 1;
    oldVnode = oldChildren[oldEnd];
    newVnode = newChildren[newEnd];
    // while循环从后向前遍历,直到遇到拥有不同key值的节点为止
    while (oldVnode.key === newVnode.key) {
        patch(oldVnode, newVnode, container);
        oldEnd--;
        newEnd--;
        oldVnode = oldChildren[oldEnd];
        newVnode = newChildren[newEnd];
    }

    // 预处理完毕后,如果满足如下条件,说明还有未被挂载的新增节点
    if (j > oldEnd && j <= newEnd) {
        // 锚点索引
        const anchorIndex = newEnd + 1;
        // 锚点元素
        const anchor = anchorIndex < newChildren.length
            ? newChildren[anchorIndex].el : null;
        // 采用while循环,逐个挂载新增节点
        while (j <= newEnd) {
            patch(null, newChildren[j++], container, anchor);
        }
    } else if (j > newEnd && j <= oldEnd) {
        // 预处理完毕后,如果满足如下条件,说明还有未被卸载的旧节点
        while (j <= oldEnd) {
            unmount(oldChildren[j++]);
        }
    } else {
        // 构造 source数组,保存新vnode中剩余未处理节点的数量
        const count = newEnd - j + 1;
        const source = new Array(count);
        source.fill(-1);

        // 起始索引
        const oldStart = j;
        const newStart = j;
        // 新增两个变量moved和pos
        let moved = false;
        let pos = 0;
        // 构建索引表
        const keyIndex = {};
        for (let i = newStart; i <= newEnd; i++) {
            keyIndex[newChildren[i].key] = i;
        }
        // 新增 patched变量,代表更新过的节点数量
        let patched = 0;
        for (let i = oldStart; i <= oldEnd; i++) {
            oldVnode = oldChildren[i];
            // 如果更新过的vnode数量 小于 需要更新的vnode数量,则执行更新
            if (patched <= count) {
                const k = keyIndex[oldVnode.key];
                if (typeof k !== 'undefined') {
                    newVnode = newChildren[k];
                    patch(oldVnode, newVnode, container);
                    source[k - newStart] = i;
                    // 判断节点是否需要移动
                    if (k < pos) {
                        moved = true;
                    } else {
                        pos = k;
                    }
                } else {
                    // 没找到
                    unmount(oldVnode);
                }
            } else {
                // 如果更新过的vnode数量 大于 需要更新的vnode数量,则卸载多余节点
                unmount(oldVnode);
            }
        }
        if (moved) {
            // 计算最长递增子序列
            const seq = lis(source);
            let s = seq.length - 1;
            let i = count - 1;
            // for循环使得i递减，按照图中箭头的方向移动
            for (i; i >= 0; i--) {
                // 说明索引为i的节点是全新节点,将其挂载
                if (source[i] === -1) {
                    // 该节点在新vnode中的真实位置索引
                    const pos = i + newStart;
                    const newVnode = newChildren[pos];
                    // 该节点的下一个节点的位置索引
                    const nextPos = pos + 1;
                    // 锚点
                    const anchor = nextPos < newChildren.length
                        ? newChildren[nextPos].el
                        : null;
                    // 挂载
                    patch(null, newVnode, container, anchor);
                } else if (i !== seq[s]) {
                    // 该节点需要移动
                    const pos = i + newStart;
                    const newVnode = newChildren[pos];
                    const nextPos = pos + 1;
                    const anchor = nextPos < newChildren.length
                        ? newChildren[nextPos].el : null;
                    insert(newVnode.el, container, anchor);
                } else {
                    // 该节点不需要移动,只需要让s指向下一个位置
                    s--;
                }
            }
        }
    }
}