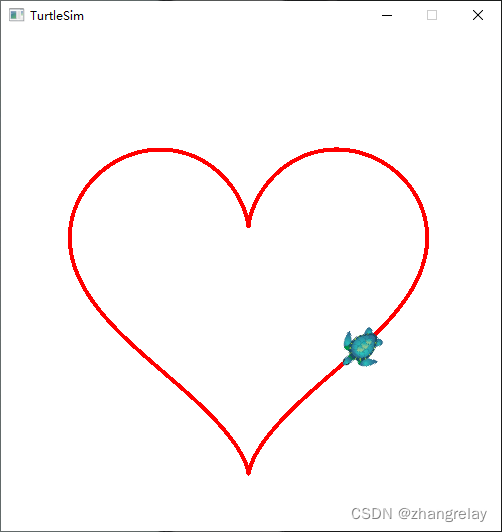
---

 

---

第一步：找到曲线数学描述的网址。

阅读后了解曲线所对应的x+y函数。

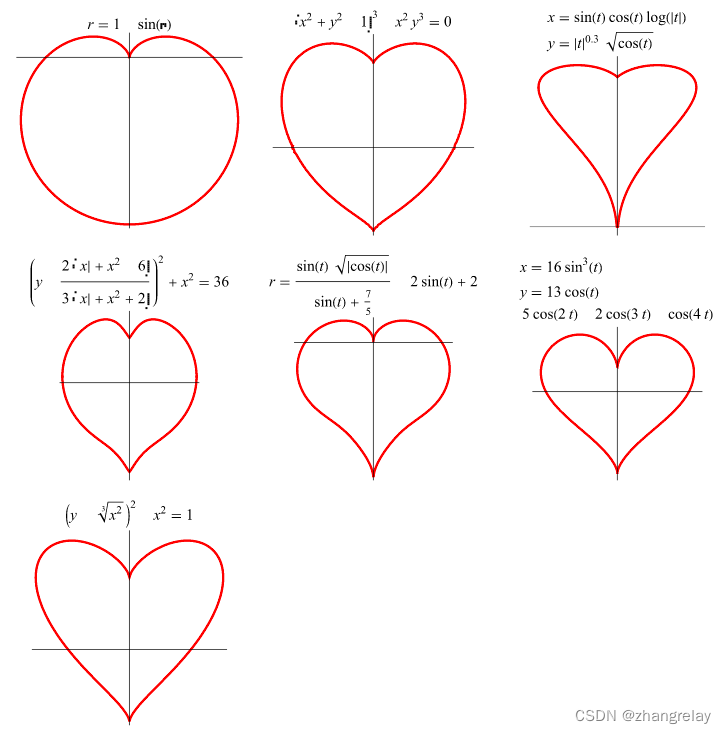
不要选太复杂的，毕竟先复现出来最重要的。

 

第二步，这个函数转为C++代码。

    //Love
    goal_x=5.5+4.0*pow(sin(curve_t/200.0),3);
    goal_y=5.5+((13.0*cos(curve_t/200.0)-5.0*cos(curve_t/100.0)-2.0*cos(3.0*curve_t/200.0)-cos(curve_t/50.0))/4.0);

 

代码解释：

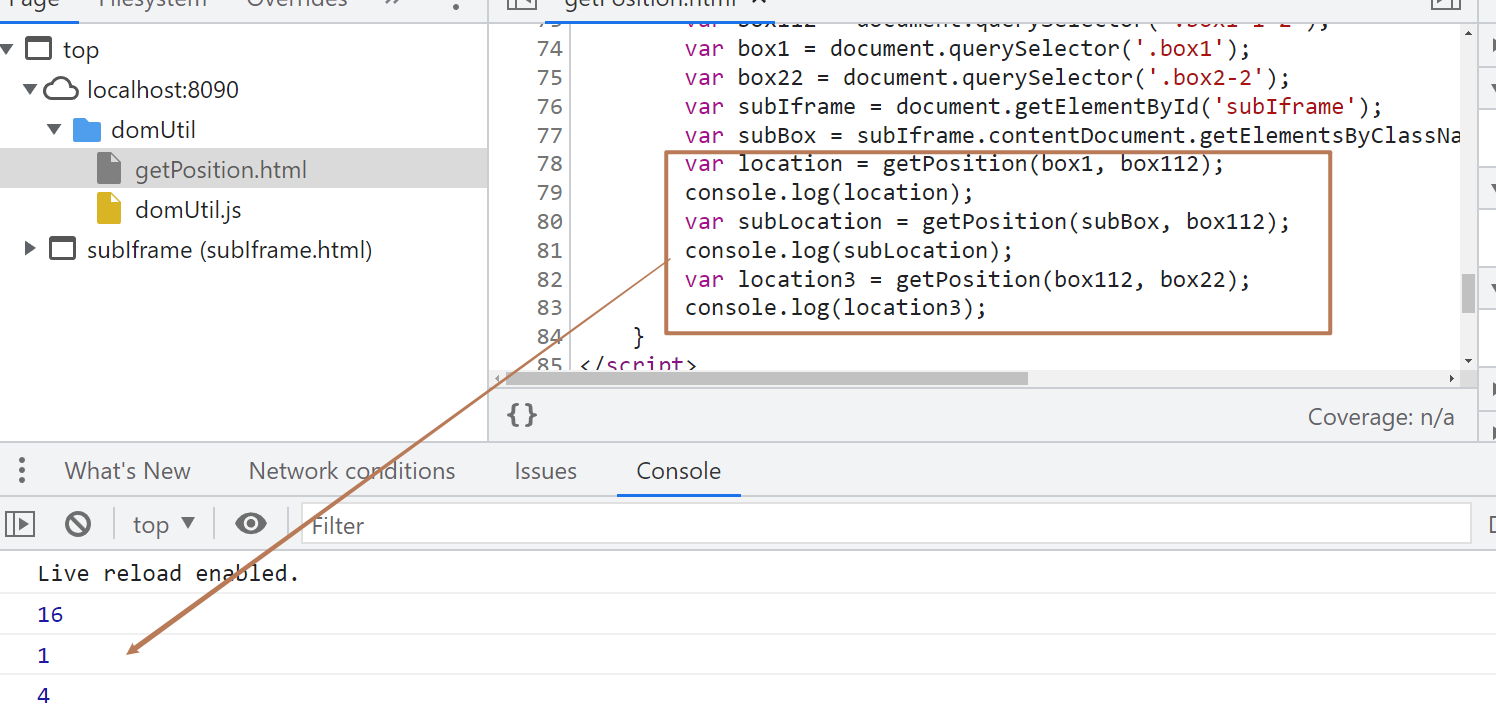
数值：5.5。对应如下

[ INFO] [1671081347.479062900]: Spawning turtle [turtle1] at x=[5.544445], y=[5.544445], theta=[0.000000]  

 

公式中的：t，代码中对应curve_t/200.0。

连续时间函数t，转为计算机离散的量，仅此而已。

公式中所绘制心形太大，代码中按比例缩小到25%。

完成后，需要将代码编译。

第三步，修改CMakelist：

add_executable(love tutorials/love.cpp)
target_link_libraries(love ${catkin_LIBRARIES})
add_dependencies(love turtlesim_gencpp)

 使用catkin_make：

Scanning dependencies of target love                                                                                    

Building CXX object turtlesim/CMakeFiles/love.dir/tutorials/love.cpp.obj                                         love.cpp                                                                                                                

Linking CXX executable D:\ros1\cocube\devel\lib\turtlesim\love.exe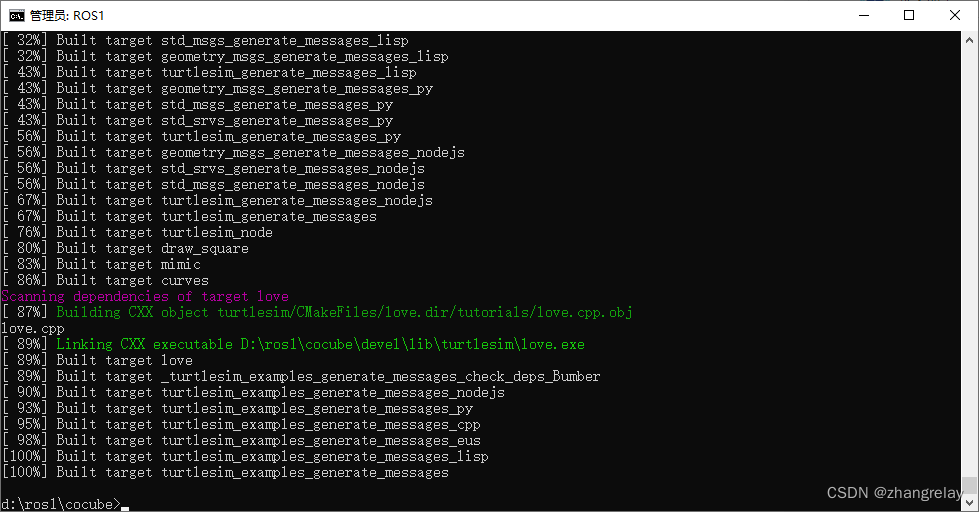 

第四步，测试：

如果出现卡顿，重启全部。

 

同样，换一个数学模型，就可以绘制更多的轨迹。 

如果觉得心形绘制不够美丽，修改参数或者函数可以获得更多类型，总有一款适合。

 

---

视频全程录制：

 

---

 

 

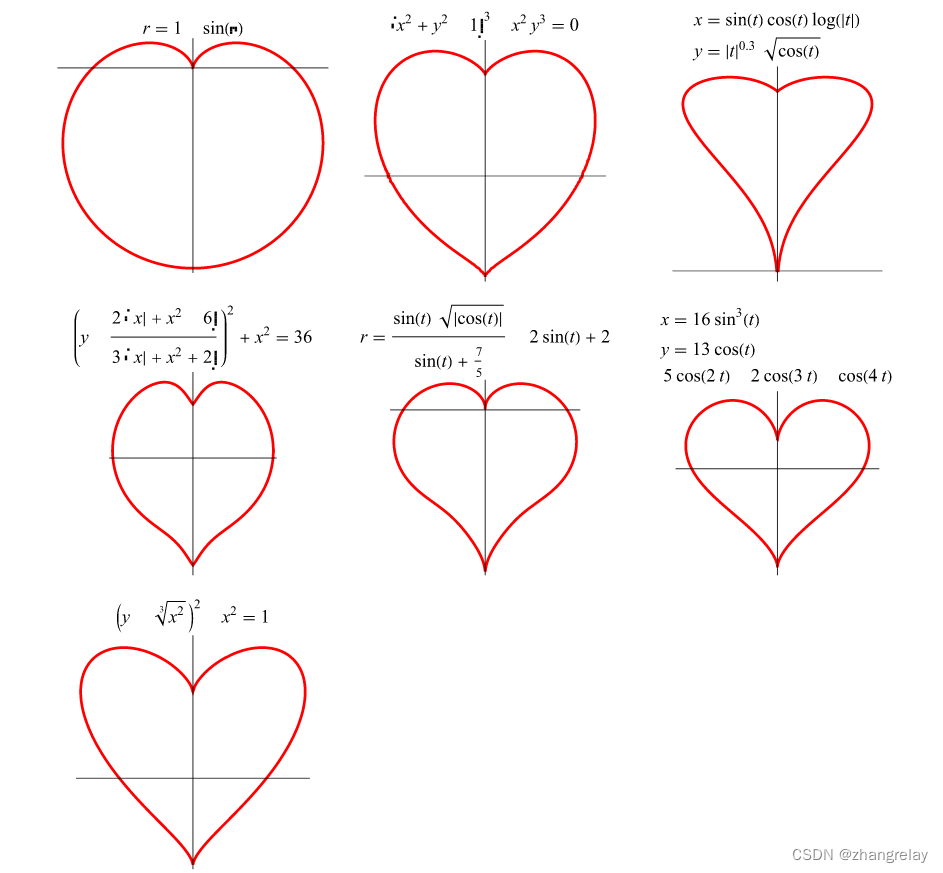
有许多数学曲线可以产生心形，其中一些在上面进行了说明。“第零”曲线是由极性方程给出的旋转心形（其名称的意思是“心形”）

通过取心脏表面的y=0横截面并将z坐标重新标记为y，得到第一条心脏曲线，给出6阶代数方程

第二条心脏曲线由参数方程给出

 
其中t在[-1,1]中（H.Dascanio，pers.comm.，2003年6月21日）。
第三条心脏曲线由下式给出

 
（P.Kuriscak，个人通讯，2006年2月12日）。该心脏曲线的每一半是6阶代数曲线的一部分。
HeartCurve5

 

第四条曲线是极曲线

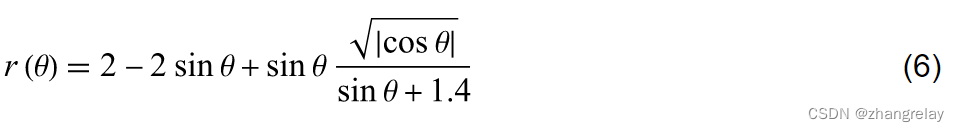
由于匿名来源，2010年2月初从Wolfram|Alpha的日志文件中获得。该心脏曲线的每一半是12阶代数曲线的一部分，因此整个曲线是24阶代数曲线。
第五心脏曲线可以参数化地定义为

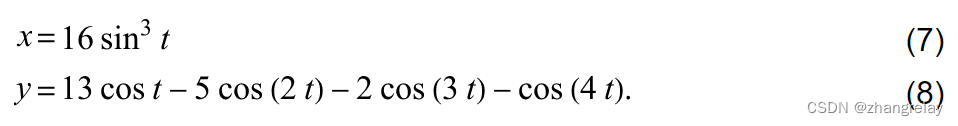
第六条心脏曲线由以下简单表达式给出

 
（由J.Schroeder于2021 10月16日在贺卡上注明）。当用比例参数a和b适当地进行无量纲化时，曲线变为

 
它可以写成x和y中的六分方程。
这些心脏的区域是

 
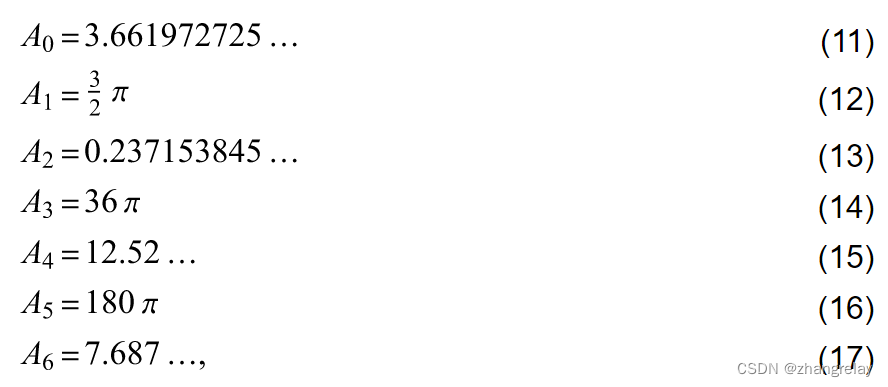
其中A_4可以作为超几何函数、反切线和伽马函数的复杂组合以封闭形式给出。

 

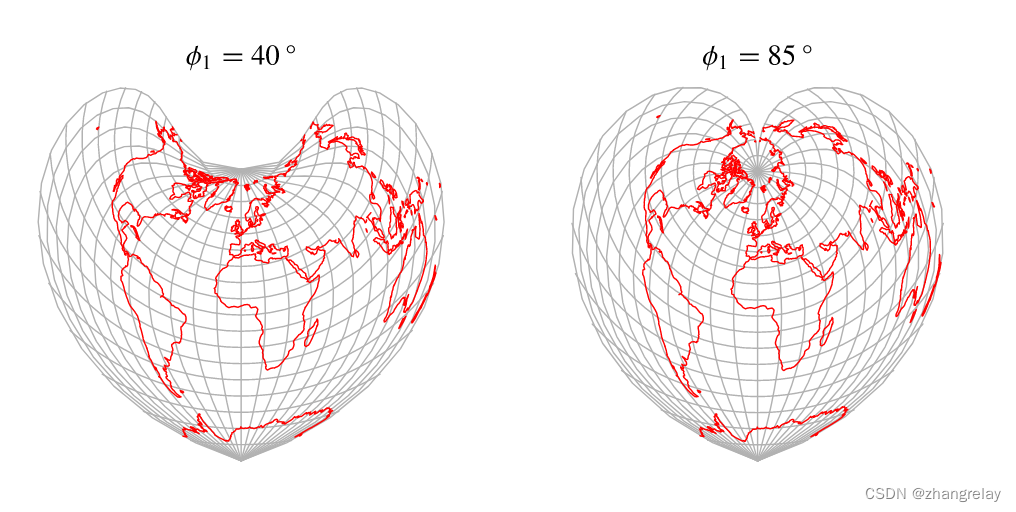
邦尼投影
Bonne投影是一种将球体表面映射到心形区域的地图投影，如上图所示。

---

♥心形曲线：

mathworld.wolfram.com/HeartCurve.html

扩展阅读：

优美的曲线（含蝴蝶线）-CoCube

---