UID: 20221214170009
aliases:
tags:
source:
cssclass:
created: 2022-12-14
1. 节点位置关系
两个节点A、B之间的位置关系总共有几种?我们第一时间能想到的:
- 节点A在节点B之后
- 节点A在节点B之前
- 节点A包含节点B
- 节点A被节点B包含
除此之外,还有两种可能:
- 节点A与节点B是同一个节点,所以他们位置关系为相同
- 节点A与节点B处于不同的文档中。
2. 节点位置算法
那么给定两个节点nodeA 和 nodeB,如何判断nodeA相对于 nodeB的位置呢?
首先,我们能想到的肯定是判断他们是否是同一个节点,这个简单,使用全等就可以判断:
nodeA === nodeB
接下来我们该去判断包含关系还是前后关系还是是否同文档关系呢?
我们先看下以上三种关系分别需要做什么:
判断包含关系,需要分别遍历nodeA 和 nodeB的祖先节点,如果其中任何一个祖先节点与对方相等,即:
// 伪代码
one of ancestorsOfnodeA === nodeB or one of ancestorsOfnodeB === nodeA
// ancestorsOfnodeA nodeA的祖先节点
// ancestorsOfnodeB nodeB的祖先节点
就可以判断他们之间存在包含关系。
要判断前后关系,则需要先遍历nodeA 之后的兄弟节点,如果其中一个节点与nodeB相等,则说明nodeA 在 nodeB 之前,然后再遍历nodeA之前的兄弟节点,如果其中一个节点nodeB相同,则nodeA在nodeB之后
要判断是否不属于同一文档,则需要满足以下条件:
nodeA与nodeB互不包含nodeA与nodeB的根节点不是同一个节点
那么判断文档关系一定是在判断包含关系之后的,那到底是先判断前后关系还是先判断包含关系呢?
- 如果先判定前后关系,需要遍历两次(前后各一次),如果不存在前后关系,那么需要接下来在判断包含关系时也依旧要遍历两次(两个节点各一次)
- 如果先判定包含关系,需要先遍历两次(两个节点各一次),如果不存在包含关系,那么接下来可以直接判定是否属于同一文档,如果属于同一文档,最后我们只需要在判断前后关系时再遍历一次(向后一次),就可以确定结果了,因为如果不在后,加之排除了之前所有情况,最后只能是在前,就不需要遍历了。
算法流程图如下:
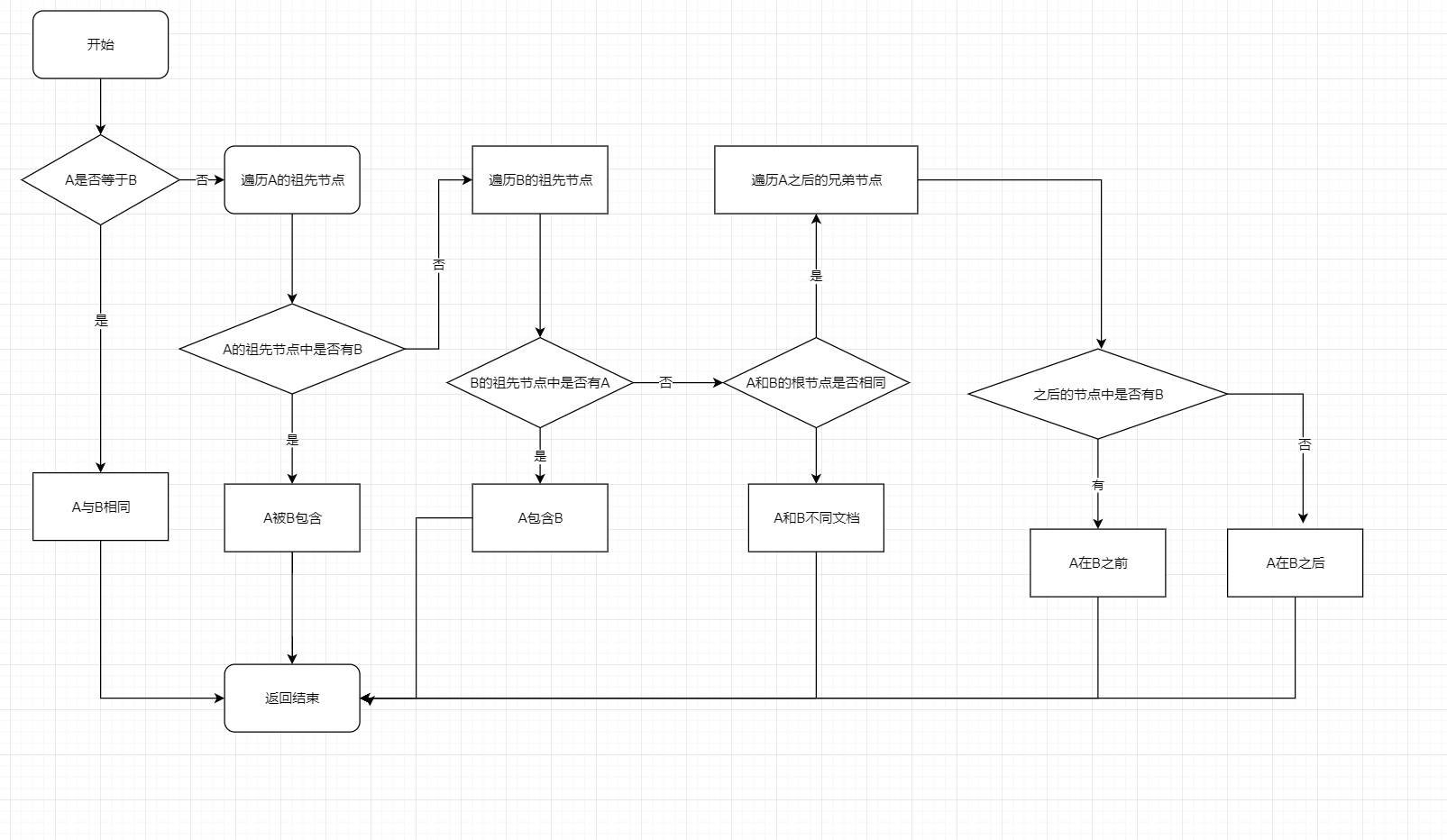
3. 算法实现
3.1 按照算法流程图依次实现
function getPosition(nodeA, nodeB){
// 首先定义位置关系的映射值:
/**
POSITION_IDENTICAL:0, // 元素相同
POSITION_DISCONNECTED:1, // 两个节点在不同文档中
POSITION_FOLLOWING:2, // 节点A在节点B之后
POSITION_PRECEDING:4, // 节点A在节点B之前
POSITION_IS_CONTAINED:8, // 节点A被节点B包含
POSITION_CONTAINS:16, // 节点A包含节点B
*/
// 判断相等关系
// A是否等于B
if (nodeA === nodeB) {
return 0;
}
// 判断包含关系
var node; // 当前循环中用来比对的node
// 遍历A的祖先节点
node = nodeA;
while (node = node.parentNode) {
if (node === nodeB) {
return 8;
}
}
// 遍历B的祖先节点
node = nodeB;
while(node = node.parentNode) {
if (node === nodeA) {
return 16;
}
}
// 判断是否属于同一文档
// 寻找A的根节点
node = nodeA;
var rootA;
while(node = node.parentNode) {
if(!node.parentNode) {
rootA = node;
}
}
// 寻找B的根节点
node = nodeB;
var rootB;
while(node = node.parentNode) {
if(!node.parentNode) {
rootB = node;
}
}
if (rootA !== rootB) {
return 1;
}
// 判断前后关系
node = nodeA;
while (node = node.nextSibling) {
if (node === nodeB) {
return 4;
}
}
return 2;
}
先验证一下:
<body>
<div class="box1">
<div class="box1-1">
<div class="box1-1-1"></div>
<div class="box1-1-2"></div>
</div>
<div class="box1-2">
<div class="box1-2-1"></div>
<div class="box1-2-2"></div>
</div>
</div>
<div class="box2">
<div class="box2-1">
<div class="box2-1-1"></div>
<div class="box2-1-2"></div>
<div class="box2-1-3"></div>
</div>
<div class="box2-2">
<iframe src="./subIframe.html" id="subIframe" width="100%" height="100%" frameborder="0" scrolling="no"></iframe>
</div>
<div class="box2-3"></div>
</div>
</body>
<script src="./domUtil.js"></script>
<script>
window.onload = function () {
var box112 = document.querySelector('.box1-1-2');
var box1 = document.querySelector('.box1');
var box22 = document.querySelector('.box2-2');
var subIframe = document.getElementById('subIframe');
var subBox = subIframe.contentDocument.getElementsByClassName('sub-box-1')[0];
var location = getPosition(box1, box112);
console.log(location);
var subLocation = getPosition(subBox, box112);
console.log(subLocation);
var location3 = getPosition(box112, box22);
console.log(location3);
}
</script>
我们选了三对节点,根据HTML的树结构和我们的位置关系映射定义,我们知道:
- box1 包含 box112,所以应该返回16;
- subBox 与 box112属于不同的文档,所以应该返回1
- box112 在 box22 的前面,所以应该返回 4
我们看下结果
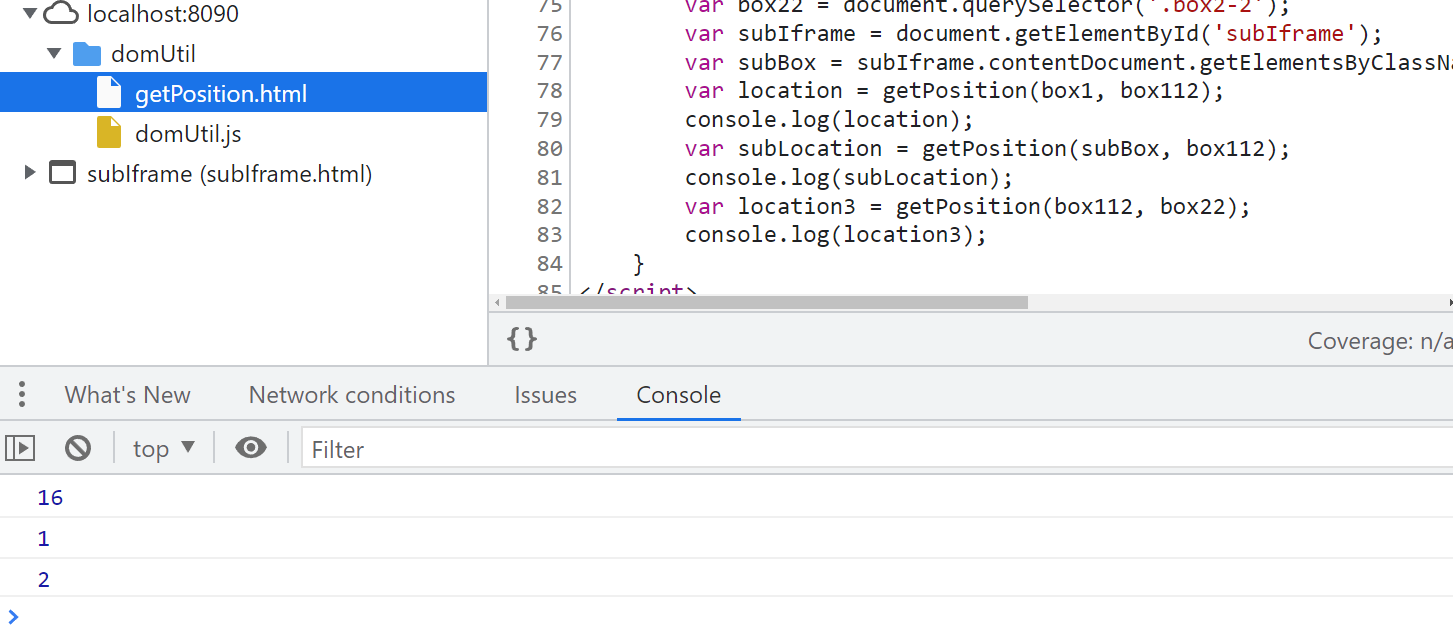
对于前后关系的判定,结果与我们期望的不符。
再看这段判断前后关系的代码
node = nodeA;
while (node = node.nextSibling) {
if (node === nodeB) {
return 4;
}
}
这里的处理方式是不对的,因为它只考虑了节点B是节点A的同级兄弟节点的情况,而没有考虑到节点B可能是节点A的祖先节点的兄弟节点或子节点,再或者是祖先节点的兄弟节点的子节点这种情况。
3.2 代码优化和修改
在上面的实现中,我们还可以发现,在判定是否同文档时分别遍历了nodeA与nodeB的祖先节点以便寻找它们的根节点,而在判定包含关系的时候,其实我们已经遍历过一次了。
所以,我们可以在判断包含关系时将这些祖先节点缓存起来,在判断同文档关系时就不需要再遍历了。
同样,缓存起来的祖先节点在判断前后关系时也可以用来辅助判断节点B是否是节点A的祖先节点的兄弟节点或子节点的情况。
function getPosition(nodeA, nodeB){
// 首先定义位置关系的映射值:
/**
POSITION_IDENTICAL:0, // 元素相同
POSITION_DISCONNECTED:1, // 两个节点在不同文档中
POSITION_FOLLOWING:2, // 节点A在节点B之后
POSITION_PRECEDING:4, // 节点A在节点B之前
POSITION_IS_CONTAINED:8, // 节点A被节点B包含
POSITION_CONTAINS:16, // 节点A包含节点B
*/
// 判断相等关系
// A是否等于B
if (nodeA === nodeB) {
return 0;
}
// 判断包含关系
var node; // 当前循环中用来比对的node
var parentsA = [nodeA],
parentsB = [nodeB],
// 遍历A的祖先节点
node = nodeA;
while (node = node.parentNode) {
if (node === nodeB) {
return 8;
}
parentsA.push(node);
}
// 遍历B的祖先节点
node = nodeB;
while(node = node.parentNode) {
if (node === nodeA) {
return 16;
}
parentsB.push(node);
}
// 判断是否属于同一文档, parentsA和parentsB中已经包含了nodeA和nodeB的根节点
parentsA.reverse();
parentsB.reverse();
if (parentsA[0] !== parentsB[0]) {
return 1;
}
// 判断前后关系
var i = -1;
while (i++, parentsA[i] === parentsB[i]) {}
nodeA = parentsA[i];
nodeB = parentsB[i];
while (nodeA = nodeA.nextSibling) {
if (nodeA === nodeB) {
return 4;
}
}
return 2;
}
我们看下这次修改的核心要点,在判断包含关系遍历两个节点的祖先节点时,将这些祖先节点依次推入祖先节点数组。然后等两个节点的祖先节点都遍历结束,没有包含关系时,我们就要开始判断是否处于同一文档,而满足不在同一文档的两个要求,第一个,互不包含已经满足,第二个,两个节点的根节点不是同一个节点,需要判断。
此时,我们有两个数组,分别是两个节点的所有祖先节点,而每个数组的最后一个元素一定就是这两个节点的根节点,所以我们只需要判断两个数组的最后一个元素是否全等就可以了:
if parentsA[parentsA.length-1] === parentsB[parentsB.length-1]
或者,我们可以反转两个数组,让两个数组的最后一个元素变为第一个元素,然后比较两个数组的第一个元素是否全等:
parentsA.reverse();
parentsB.reverse();
if parentsA[0] !== parentsB[0]
这两种写法都可以,从理论上来说,第一种只需要一条语句,而第二种需要三条语句,本来选第一种更好,但是由于我们接下来判断前后关系的时候,也需要用到这两个数组,并且需要将两个数组进行翻转,所以我们就使用了第二种写法。
下面我们就来看下最后判断前后关系的算法。
当走到判断前后关系这一步时,我们已经可以确定:
- A和B不是同一个元素
- A和B互不包含
- A和B属于同一个文档
此时,剩余的可能就是
- A和B是兄弟节点,它们有同一个父节点,这种情况下,往上所有的祖先节点都相同
- A和B不是兄弟节点,但A的某个祖先节点和B的某个祖先节点是同一个节点,也就是A和B有相同的祖先节点。
这两种情况的共同点在于: A和B有相同的祖先节点。

上图的DOM树结构中,B11与B21,B11与B12,A1与C1,都符合上述关系描述。
此时,我们需要的内容变成了: A和B的最近的一个共同祖先节点下一层两个分属A和B的祖先节点(或A和B本身)谁先谁后。
比如:
- B11与B21,只需要找到它们最近的共同祖先节点B,然后在B的下一层里,B1是B11的祖先节点,B2是B21的祖先节点,只要遍历B1的兄弟节点,其中有B2,根据遍历方向就能确定它们的前后关系
- B11与B12,找到它们最近的的共同祖先节点B1,这个节点下一层就是B11和B12,只要遍历B11的兄弟节点,其中有B12,那么也能确定它们的前后关系
- A1与C1,找打它们最近的共同祖先节点根节点,在根节点下一层,A是A1的祖先节点,C是C1的祖先节点,遍历A的兄弟节点,只要其中有C,那么根据遍历方向也可以确定它们的前后关系。
具体实现:
- 找到最近的祖先节点
- 在最近祖先节点下一层,分别找到A和B的祖先节点A1和B1(也可能就是他们自身,比如上例中B11与B12)
- 向后遍历A1节点的兄弟节点,如果其中一个是B1,就可以确定A1在B1前面,如果没有,那就是B1在A1前面
- A1相对于B1的前后关系就是A相对于B的前后关系
在前面判断包含关系时,我们得到了A与B的祖先节点数组,那两个数组里元素的顺序是顺着DOM树由下而上的,最后一个元素是根节点,然而我们要找A与B两个节点的最近的共同祖先节点,最好是顺着DOM树由上而下找,这样确保A数组与B数组中最开始的元素,下标相同的元素指向同一个节点
比如上例中的A1 与 B21,
在判断完包含关系后,得到两个数组:
parentsA = [A1, A, root]; // A1 的祖先节点数组
parentsB = [B21, B2, B, root]; // B21 的祖先节点数组
可以看到,这两个数组长度不一致,要想找到它们最近的共同祖先节点,对于两个不同长度的数组,可能需要嵌套循环对比来实现。
而如果我们将其反转为:
parentsA = [root, A, A1]; // A1 的祖先节点数组
parentsB = [root, B, B2, B21]; // B21 的祖先节点数组
现在我们找它们最近的共同祖先节点就好找多了,只要使用相同的下标,遍历两个数组,直到相同下标的元素不相等,就说明上一个下标对应的元素就是最近的共同祖先元素,而当前下标对应的两个元素恰好就是最新的共同祖先元素下分属A1与B21的祖先节点。
比如下标初始是-1,
下标+1 = 0,那parentsA[0] === parentsB[0] === root
然后下标再+1 = 1, 此时 parentsA[1] 为A,parentsB[1]为B,两个不相等,此时我们其实就已经找到了A1和B21最新的共同祖先节点(root)下一层分属它们的祖先节点(A,B)
所以在判定是否属于同一文档时,我们直接选择了反转这两个数组。
反转后寻找最近共同祖先节点下一层分属两个节点的父节点的具体代码实现:
var i = -1
// 遍历,下标自增,直到 parentsA[i] !== parentsB[i]时停止,得到最近的不同祖先节点的下标
while (i++, parentsA[i] === parentsB[i]) {}
nodeA = parentsA[i];
nodeB = parentsB[i];
接下来就是遍历其中一个祖先节点的兄弟节点,看其中是否有另一个节点的祖先节点:
while (nodeA = nodeA.nextSibling) {
if (nodeA === nodeB) {
return 4;
}
}
修改后,我们重新运行我们的验证程序:
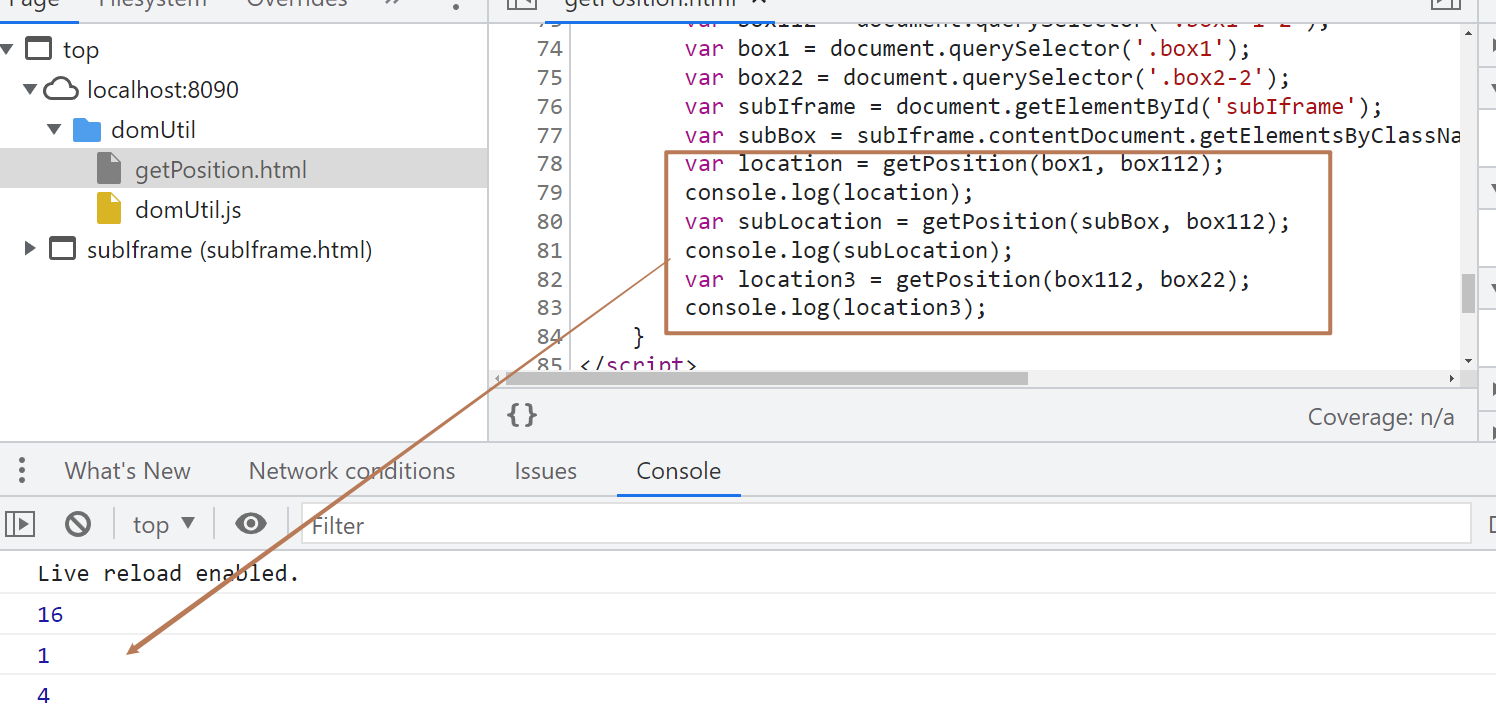
符合预期,完美!