1、题目描述

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例1：

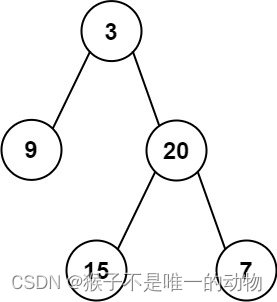
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

2、VS2019上运行

使用方法一：递归

#include <iostream>
#include <vector>
#include <unordered_map>
#include<queue>
#include<string>

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
private:
    std::unordered_map<int, int> index;

public:
    TreeNode* myBuildTree(const std::vector<int>& preorder, const std::vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        // 递归结束判断条件
        if (preorder_left > preorder_right) {
            return nullptr;
        }

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;

        // 在中序遍历中定位根节点
        int inorder_root = index[preorder[preorder_root]];

        // 先把根节点建立出来
        TreeNode* root = new TreeNode(preorder[preorder_root]);

        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;

        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);

        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);

        return root;
    }

    TreeNode* buildTree(std::vector<int>& preorder, std::vector<int>& inorder) {
        int n = preorder.size();

        // 构造哈希映射，帮助我们快速定位根节点在中序遍历中的位置
        for (int i = 0; i < n; ++i) {
            index[inorder[i]] = i;
        }

        // 递归构建二叉树
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
};

int main() {
    Solution solution;

    std::vector<int> preorder = { 3, 9, 20, 15, 7 };
    std::vector<int> inorder = { 9, 3, 15, 20, 7 };

    TreeNode* root = solution.buildTree(preorder, inorder);

    // 进行层序遍历，输出构建完成的二叉树的值
    std::queue<TreeNode*> q;
    q.push(root);

    std::vector<std::string> result; // 存储层序遍历结果

    while (!q.empty()) {
        TreeNode* node = q.front();
        q.pop();

        if (node == nullptr) {
            result.push_back("null");
        }
        else {
            result.push_back(std::to_string(node->val));
            q.push(node->left);
            q.push(node->right);
        }
    }

    // 清除尾部多余的连续的 "null"
    while (!result.empty() && result.back() == "null") {
        result.pop_back();
    }

    // 输出结果
    std::cout << "Output: [";
    for (size_t i = 0; i < result.size(); ++i) {
        std::cout << result[i];
        if (i < result.size() - 1) {
            std::cout << ",";
        }
    }
    std::cout << "]" << std::endl;

   return 0;
}

Output: [3,9,20,null,null,15,7]

3、解题思路

前序找根，后序划分
解题思路递归