参考资料:
该如何作一条已知曲线的等距曲线? - 知乎
等距线_百度百科
目录
1.等距线
2.数学推导
3.示例
4.代码与结果
1.等距线
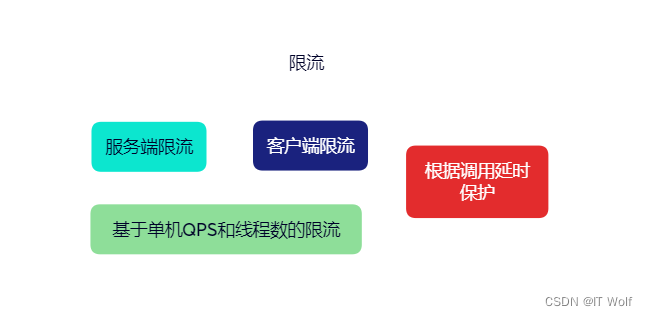
等距线(equidistant line)亦称平行曲线,一种平面曲线,即由一已知曲线所产生的另一曲线。平行曲线如下图。
|
|
|
2.数学推导
2.1 核心思想:
从原曲线法线方向偏移所需的距离,就可以得到这些平行曲线
2.2数学推导
对于参数曲线r(t),其切线速度就是其第一导数:
归一化后得单位切线矢量:
在二维中,垂直于切线的单位法矢量只需旋转切线90度,可以得到垂直于切线的单位法矢量为
那么,设偏移距离为a,r(t)的两条平行曲线为
3.示例
本文以为例,将该方程转为参数方程,得s(t)为,
对s(t)求导得v(t),
归一化后得单位切线矢量T(t),
将T(t)旋转90度得到N(t),
于是平移距离为a的曲线为,
4.代码与结果
PS:注意横、纵坐标尺度不一致,想看更明显的效果可以试验一下y=x^2
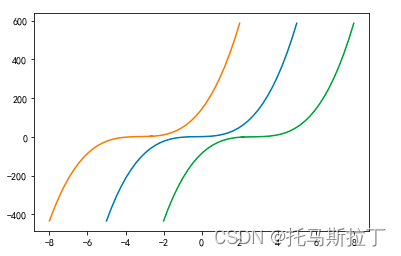
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(-5,5,40)
x1 = t
y1 = 4*t**3 + 3*t**2 + 2*t + 1
x2 = t + 3*-1*(12*t**2+6*t+2)/np.sqrt(1+(12*t**2+6*t+2)**2)
y2 = 4*t**3 + 3*t**2 + 2*t + 1 + 3*1/np.sqrt(1+(12*t**2+6*t+2)**2)
x3 = t - 3*-1*(12*t**2+6*t+2)/np.sqrt(1+(12*t**2+6*t+2)**2)
y3 = 4*t**3 + 3*t**2 + 2*t + 1 - 3*1/np.sqrt(1+(12*t**2+6*t+2)**2)
plt.plot(x1,y1)
plt.plot(x2,y2)
plt.plot(x3,y3)