OpenGL 学习教程
Android OpenGL ES 学习(一) – 基本概念
Android OpenGL ES 学习(二) – 图形渲染管线和GLSL
Android OpenGL ES 学习(三) – 绘制平面图形
Android OpenGL ES 学习(四) – 正交投影
Android OpenGL ES 学习(五) – 渐变色
Android OpenGL ES 学习(六) – 使用 VBO、VAO 和 EBO/IBO 优化程序
Android OpenGL ES 学习(七) – 纹理
Android OpenGL ES 学习(八) –矩阵变换
Android OpenGL ES 学习(九) – 坐标系统和。实现3D效果
代码工程地址: https://github.com/LillteZheng/OpenGLDemo.git
上一章,我们已经学习了矩阵变换,实现了一些特殊的2D效果,这一章,我们来实现更酷的效果 – 3D。效果如下:

这一章可能会稍微难理解一点,我也是看官网看了几遍,再看懂了一些。所以,这一章说说我的理解,有不对的地方,欢迎大家指正。
前面说到,OpenGL 的坐标范围为 [-1,1] 之间,所以,要求我们在赋值或者矩阵运算的时候,都要进行转换,然后放进 [-1,1] 里面。
把一个物体的顶点坐标,转换成设备坐标,再转换成屏幕坐标,它是分步进行的,也就是类似于流水线那样子。在流水线中,物体的顶点在最终转化为屏幕坐标之前,还会被变换到多个坐标系统(Coordinate System)。
理解这个过程的好处在于,我们可以理清坐标转换的过程,并在其中加入一些效果,如 3D 效果。
总的来说,OpenGL 共有5个坐标系统。
- 局部空间(Local Space,或者称为物体空间(Object Space))
- 世界空间(World Space)
- 观察空间(View Space,或者称为视觉空间(Eye Space))
- 裁剪空间(Clip Space)
- 屏幕空间(Screen Space)
这就是一个顶点在最终被转化为片段之前需要经历的所有不同状态。
一. 坐标概述
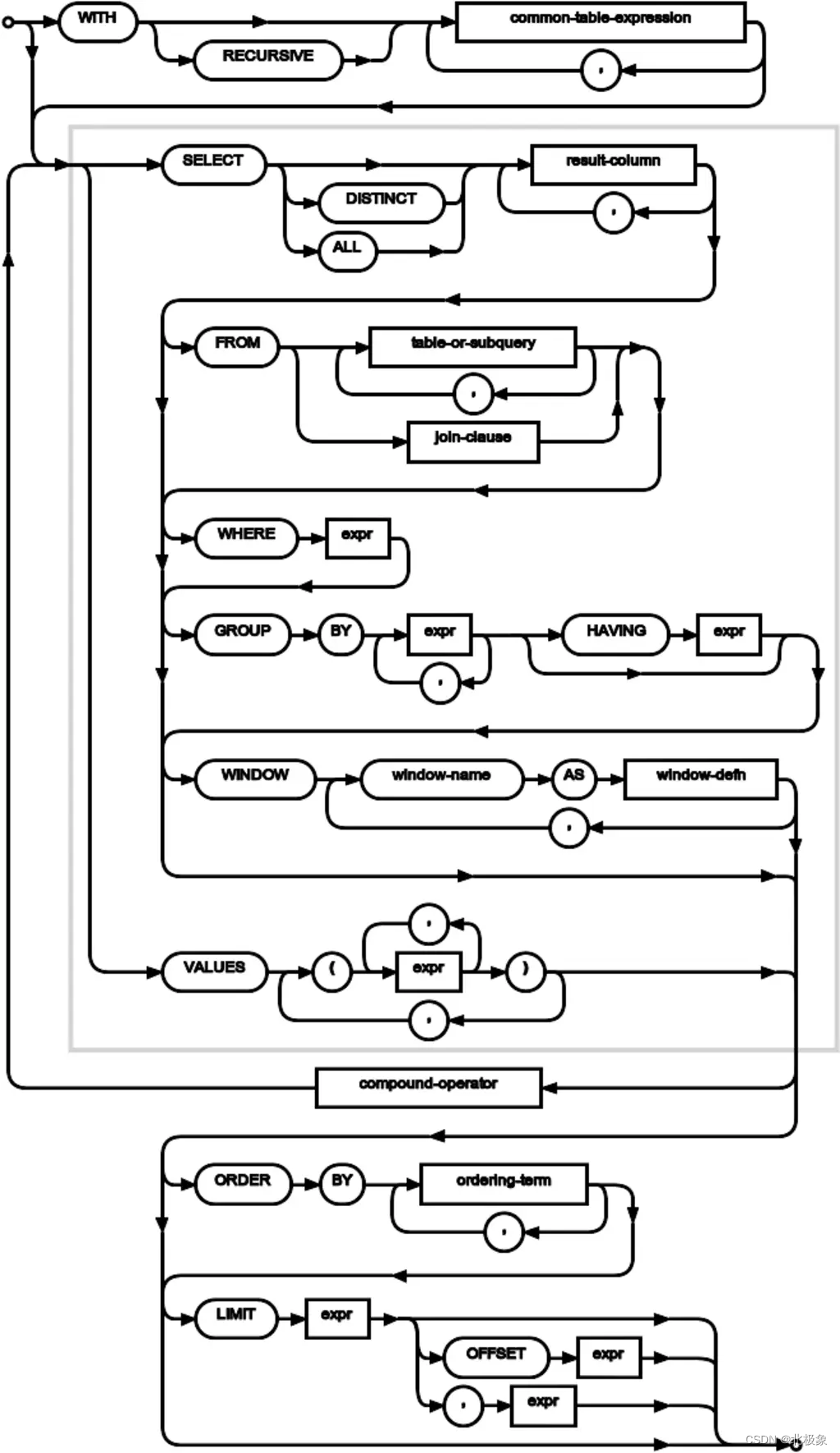
为了将坐标从一个坐标系变换到另一个坐标系,我们需要用到几个变换矩阵,最重要的几个分别是模型(Model)、观察(View)、投影(Projection)三个矩阵。我们的顶点坐标起始于局部空间(Local Space),在这里它称为局部坐标(Local Coordinate),它在之后会变为世界坐标(World Coordinate),观察坐标(View Coordinate),裁剪坐标(Clip Coordinate),并最后以屏幕坐标(Screen Coordinate)的形式结束。下面的这张图展示了整个流程以及各个变换过程做了什么:
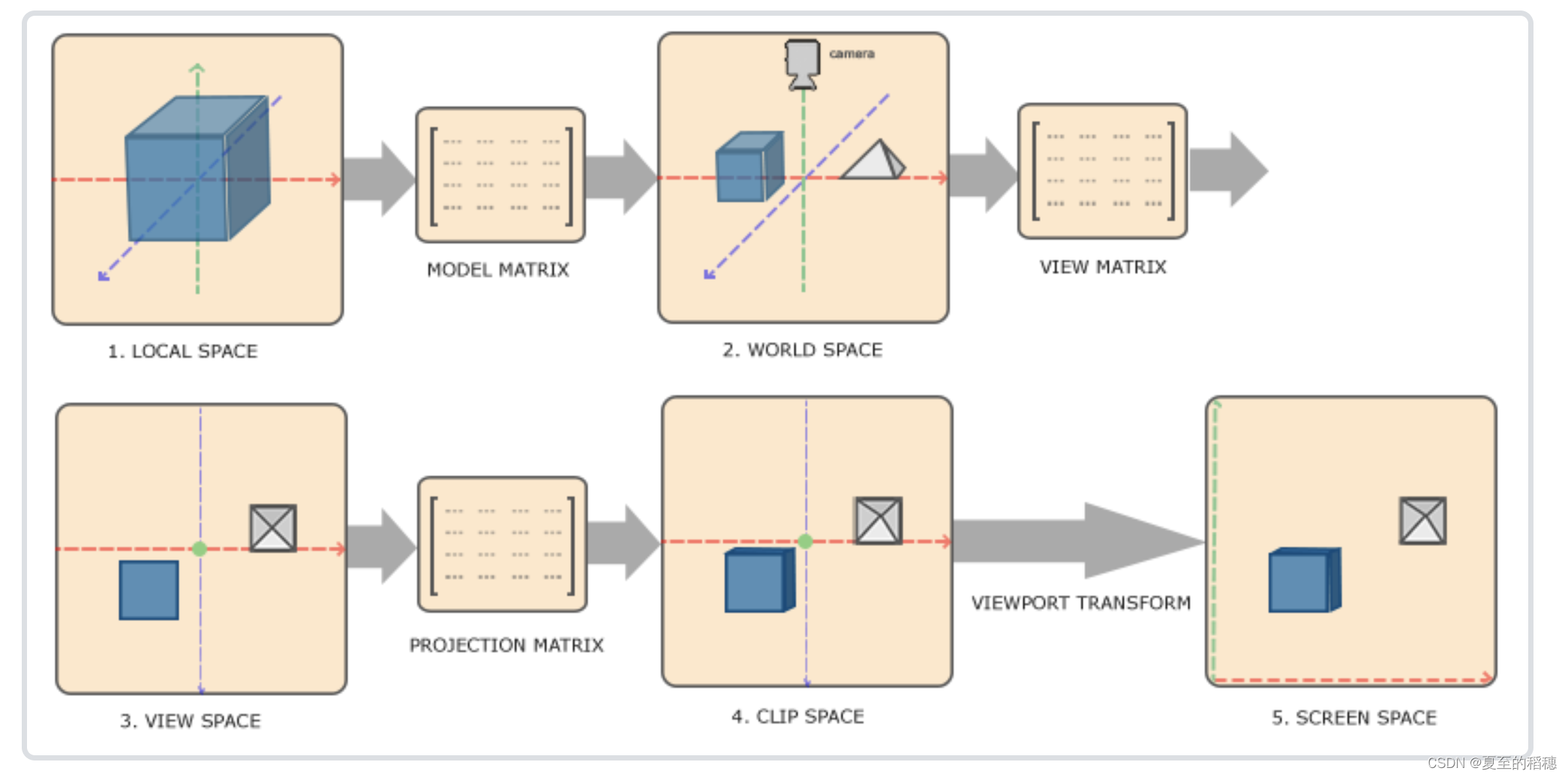
意思就是,一个物体,从一个局域坐标到屏幕坐标,需要进过一系列的矩阵变换。
下面解释一下一些专有名词:
1.1 局部空间(Local Space)
是物体相对于自身的原点的坐标,是物体的起点。但是光有这个还不行,因为它没有参照物,放哪里的都可以,所以需要与 模型矩阵 相乘,得到世界坐标。
1.2 世界空间(World Space)
世界空间坐标是一个更大的坐标,你可以随意放在哪个位置,比如放广州,或者深圳,这一步,通常通过矩阵的平移,缩放和放大来实现,但这不能描述物体的物体位置。所以需要与 观察矩阵 相乘,得到一个以人为视角的方向。
1.3 观察空间(View Space)
观察空间也叫 camrea (摄像机)空间 或 用户空间,一个物体,需要有一个观察角度,才能直观地看到这个物体,产生一个以我们为角度的坐标,相当于把物体拉到我们面前。
1.4 裁减空间(Clip Space)
在顶点着色器运行的最后,我们希望把这些坐标都放在一个特定的范围内,超过这个范围的都被裁剪掉。在正交投影那章也讲到,我们实际的屏幕肯定不是 [-1,1] ,这个范围,所以我们需要一些特殊的投影矩阵,帮我们实现把实际物理坐标转换到 [-1,1] 中。
使用投影矩阵能将3D坐标投影(Project)到很容易映射到2D的标准化设备坐标系中。
然后就可以使用 glViewport 或其他渲染模式,把最终的坐标将会被映射到屏幕空间中,并转换成片段。
将观察坐标变换为裁剪坐标的投影矩阵可以为两种不同的形式,每种形式都定义了不同的平截头体。我们可以选择创建一个正射投影矩阵(Orthographic Projection Matrix)或一个透视投影矩阵(Perspective Projection Matrix)。
1.4.1 正交投影
正交投影,你可以理解成,在用户空间视角,太阳直射这个物体,那么这个物体的影子,跟物体的大小是相等,它的平截面,就是物体本身:
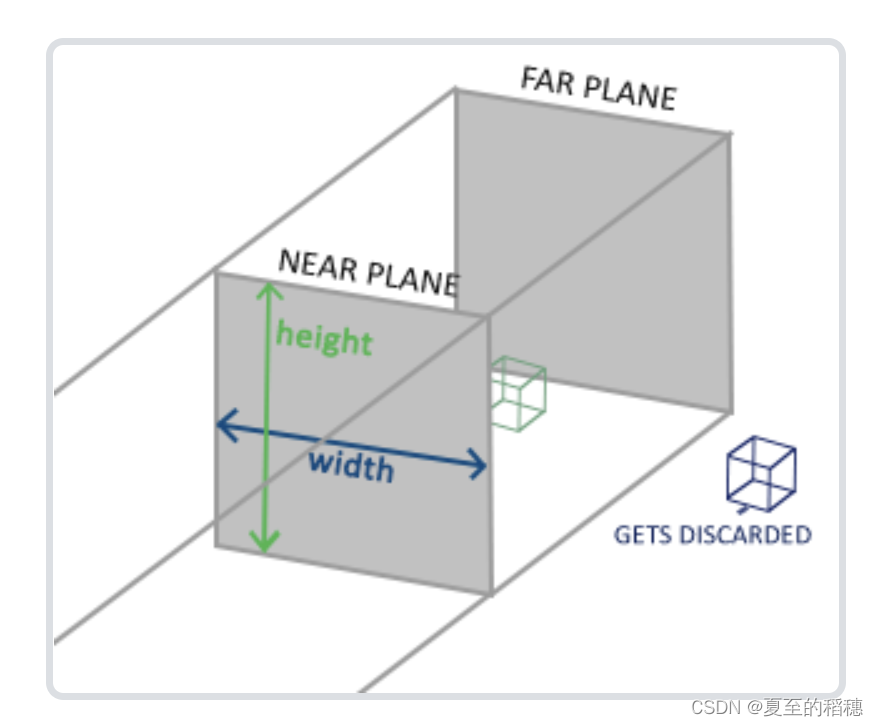
因此,当我们在画一些二维图形,发现写完坐标之后,长度不太一致,可以使用正交投影去修正 Android OpenGL ES 学习(四) – 正交投影。矩阵公式为:
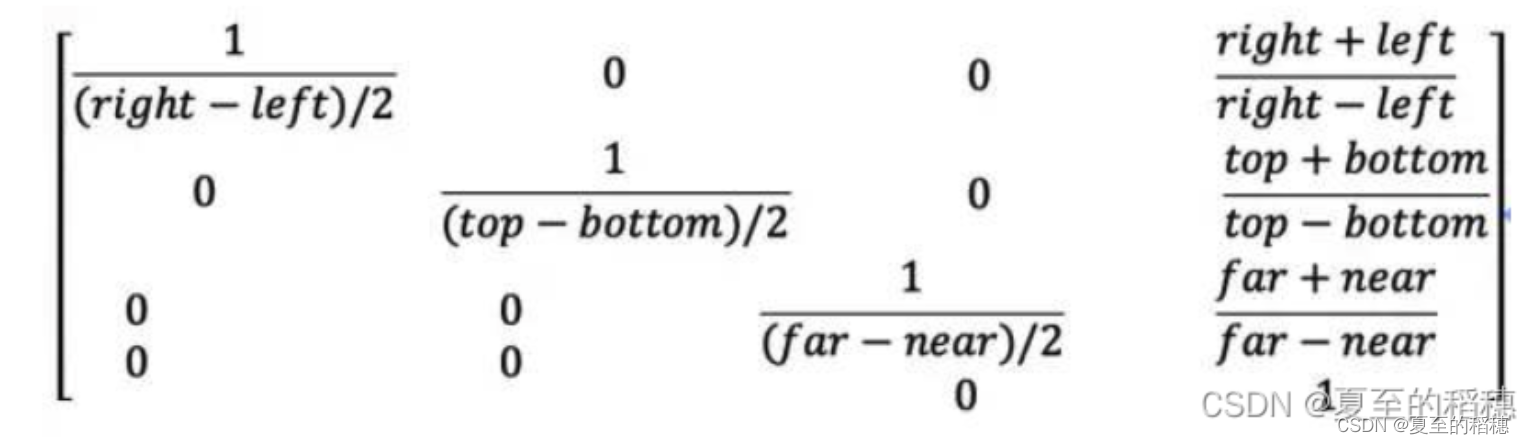
1.4.2 透视投影
在实际的生活,我们看东西,离你越远的东西看起来更小。这个奇怪的效果称之为透视(Perspective)。透视的效果在我们看一条无限长的高速公路或铁路时尤其明显,正如下面图片显示的那样:

在我们认知中,就算铁路再远,它都是两条平行线,永远不可能相交的,但在投影中,它却是可以相交的,为了实现这个理论,引入了 w 分量,也就是齐次坐标(可点击查看齐次坐标)。
我们在坐标的基础上,处于 w 分量,就能得到一个透视的效果

它的视线方法为:
Matrix.perspectiveM(projectionMatrix,0,45f,aspectRatio,0.3f,100f)
看下图:
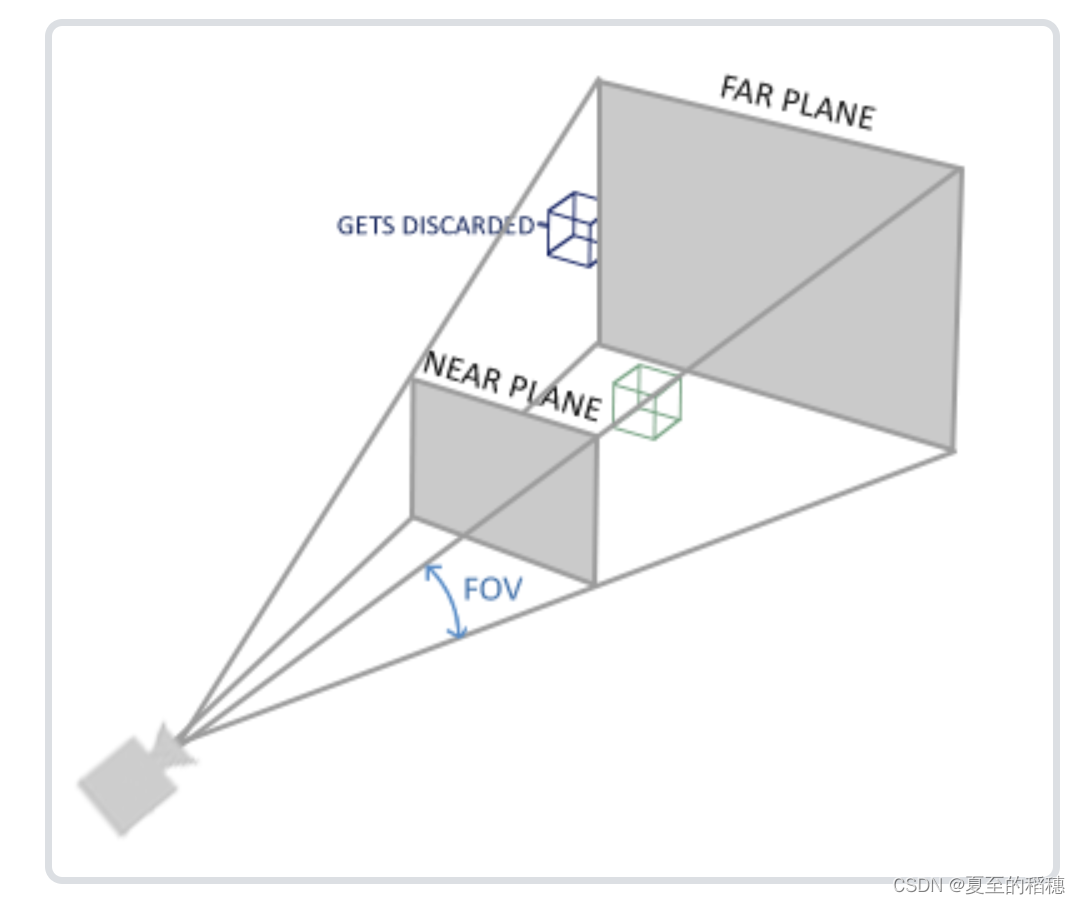
其中 fov 为视觉空间的观察角度,这样看起来比较真实,near 和 far 表示平截面的近平面和远平面,通常设置近距离为0.1f,而远距离设为100.0f,处于这个范围都会被渲染。
二. 进入3D
现在我们按照上面的步骤,实现3D 的效果,上面几个步骤组成一起是:
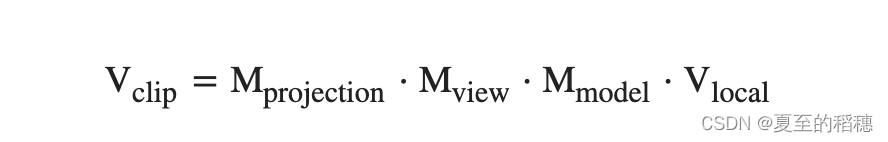
注意矩阵运算的顺序是相反的(记住我们需要从右往左阅读矩阵的乘法)。最后的顶点应该被赋值到顶点着色器中的gl_Position,OpenGL将会自动进行透视除法和裁剪。
顶点着色器保持不变,保留一个 matrix 即可,我们最后再把 model,view 和 projection 结合起来。
private const val VERTEX_SHADER = """#version 300 es
uniform mat4 u_Matrix;
layout(location = 0) in vec4 a_Position;
layout(location = 1) in vec2 aTexture;
out vec4 vTextColor;
out vec2 vTexture;
void main()
{
// 矩阵与向量相乘得到最终的位置
gl_Position = u_Matrix * a_Position;
vTexture = aTexture;
}
"""
定义一个单位矩阵,并设置 model,view,projection 和最后矩阵结果 mvpMatrix:
private fun getIdentity() = floatArrayOf(
1f, 0f, 0f, 0f,
0f, 1f, 0f, 0f,
0f, 0f, 1f, 0f,
0f, 0f, 0f, 1f
)
//获取矩阵
val modelMatrix = getIdentity()
val viewMatrix = getIdentity()
val projectionMatrix = getIdentity()
val mvpMatrix = getIdentity()
2.1 模型矩阵
首先,先使用模型矩阵,把局部空间变成世界空间:
//设置 M
Matrix.rotateM(modelMatrix,0,-55f,1f,0f,0f)
这里向x轴旋转 -55 °
2.2 视图矩阵
接着,再使用视图矩阵,将世界空间,转成视图空间:
//设置 V
Matrix.translateM(viewMatrix,0,0f,0f,-3f)
OpenGL 满足右手坐标系,所以如果要把物体往我们这边靠,就是负的,所以这里向 z 轴移动了 3f 。
2.3 投影矩阵
这里使用透视矩阵,用来模拟除以 w 分量,实现躺平效果:
//设置 P
Matrix.perspectiveM(projectionMatrix,0,45f,aspectRatio,0.1f,100f)
最后再把他们组合起来:
//组合成 mvp,先 v x m
Matrix.multiplyMM(mvpMatrix,0, viewMatrix,0, modelMatrix,0)
//然后是 p x v x m
Matrix.multiplyMM(mvpMatrix,0, projectionMatrix,0, mvpMatrix,0)
val u_Matrix = getUniform("u_Matrix")
GLES30.glUniformMatrix4fv(u_Matrix,1,false, mvpMatrix,0)
最后传入顶点着色器进行渲染。
我们的顶点坐标已经使用模型、观察和投影矩阵进行变换了,最终的物体应该会:
- 稍微向后倾斜至地板方向。
- 离我们有一些距离。
- 有透视效果(顶点越远,变得越小)

三. 3D 立方体
终于到了这个环节,为了实现一个立方体,我们需要准备36个点,6个面 x 每个面有2个三角形组成 x 每个三角形有3个顶点),这36个点可以从 这里 获取。
然后我们需要改变 GlSurface 的渲染模式,改成持续绘制:
renderMode = GLSurfaceView.RENDERMODE_CONTINUOUSLY
然后,为了不重新去计算 EBO 的三角形排列,所以,我们使用
GLES30.glDrawArrays(GLES30.GL_TRIANGLES, 0, 36)
来绘制,同理,你需要去掉 EBO 加载数据的赋值:
/* //创建 ebo
GLES30.glGenBuffers(1, ebo, 0)
//绑定 ebo 到上下文
GLES30.glBindBuffer(GLES30.GL_ELEMENT_ARRAY_BUFFER, ebo[0])
//EBO 数值
GLES30.glBufferData(
GLES30.GL_ELEMENT_ARRAY_BUFFER,
indexData.capacity() * 4,
indexData,
GLES30.GL_STATIC_DRAW
)*/
为了更好的展示,我们也让渲染角度,不断的累加,这样效果更明显,完整的代码如下:
GLES30.glClear(GLES30.GL_COLOR_BUFFER_BIT)
GLES30.glBindVertexArray(vao[0])
Matrix.setIdentityM(modelMatrix, 0)
Matrix.setIdentityM(viewMatrix, 0)
Matrix.setIdentityM(projectionMatrix, 0)
Matrix.setIdentityM(mvpMatrix, 0)
angle += 1
angle %= 360
//设置 M
Matrix.rotateM(
modelMatrix, 0,
angle,
0.5f,
1.0f,
0f
)
//设置 V
Matrix.translateM(
viewMatrix,
0,
0f,
0f,
-4f
)
//设置 P
Matrix.perspectiveM(projectionMatrix, 0, 45f, aspectRatio, 0.3f, 100f)
//组合成 mvp,先 v x m
Matrix.multiplyMM(mvpMatrix, 0, viewMatrix, 0, modelMatrix, 0)
//然后是 p x v x m
Matrix.multiplyMM(mvpMatrix, 0, projectionMatrix, 0, mvpMatrix, 0)
val u_Matrix = getUniform("u_Matrix")
GLES30.glUniformMatrix4fv(u_Matrix, 1, false, mvpMatrix, 0)
//useVaoVboAndEbo
texture?.apply {
GLES30.glBindTexture(GLES30.GL_TEXTURE_2D, id)
}
//GLES30.glDrawElements(GLES30.GL_TRIANGLE_STRIP, 6, GLES30.GL_UNSIGNED_INT, 0)
GLES30.glDrawArrays(GLES30.GL_TRIANGLES, 0, 36)

咦,看起来有点奇怪,怎么感觉所有面都有点穿插了,立方体的某些本应被遮挡住的面被绘制在了这个立方体其他面之上。
之所以会这样,是因为 OpenGL 绘制时,会覆盖之前的像素,所以有些三角形就覆盖在部分三角形上了。
处理这个也比较方便,就是开始 Z 缓冲。
3.1 Z缓冲
Z缓冲也叫深度缓冲(Depth Buffer),看官网怎么解释:
GLFW会自动为你生成这样一个缓冲(就像它也有一个颜色缓冲来存储输出图像的颜色)。深度值存储在每个片段里面(作为片段的z值),当片段想要输出它的颜色时,OpenGL会将它的深度值和z缓冲进行比较,如果当前的片段在其它片段之后,它将会被丢弃,否则将会覆盖。这个过程称为深度测试(Depth Testing),它是由OpenGL自动完成的。
什么意思呢,比如第一个已经绘制了一个矩形,OpenGL 也会有一个颜色缓冲,但第二个在画的时候,发现前面已经有缓存了,OK,那我就画没被缓存或者说遮挡的部分。
默认它是关闭,所以需要打开:
//开启z轴缓冲,深度测试
GLES30.glEnable(GLES30.GL_DEPTH_TEST)
因为我们使用了深度测试,我们也想要在每次渲染迭代之前清除深度缓冲(否则前一帧的深度信息仍然保存在缓冲中)。就像清除颜色缓冲一样,我们可以通过在glClear函数中指定DEPTH_BUFFER_BIT位来清除深度缓冲:
GLES30.glClear(GLES30.GL_COLOR_BUFFER_BIT or GLES30.GL_DEPTH_BUFFER_BIT)
效果:

3.2 渲染多个矩形
现在我们想画更多的立方体,每个立方体看起来都是一样的,区别在于它们在世界的位置及旋转角度不同。
所以,我们只需要改变的它模型矩阵就可以了,但我们又像让每个立方体有大小之分,所以也改变它的视图矩阵,这样跟清晰点。
由于屏幕不大,我们设置4个立方体,它的位置如下:
var mulPosition = floatArrayOf(
0.0f, 0.0f, 0.0f,
1.2f, 1.2f, -1.0f,
-1.5f, -1.3f, -2.5f,
-1.3f, 1.3f, -1.5f
)
然后 for 循环中,去把每个分量的值拿出来即可。
for (i in 0..boxCount) {
Matrix.setIdentityM(modelMatrix, 0)
Matrix.setIdentityM(viewMatrix, 0)
Matrix.setIdentityM(projectionMatrix, 0)
Matrix.setIdentityM(mvpMatrix, 0)
angle += 1
angle %= 360
//设置 M
Matrix.rotateM(
modelMatrix, 0,
angle,
mulPosition[i * 3] + 0.5f,
mulPosition[i * 3 + 1] + 1.0f,
mulPosition[i * 3 + 2]
)
//设置 V
Matrix.translateM(
viewMatrix,
0,
mulPosition[i * 3],
mulPosition[i * 3 + 1],
mulPosition[i * 3 + 2] - 4f - boxCount
)
//设置 P
Matrix.perspectiveM(projectionMatrix, 0, 45f, aspectRatio, 0.3f, 100f)
//组合成 mvp,先 v x m
Matrix.multiplyMM(mvpMatrix, 0, viewMatrix, 0, modelMatrix, 0)
//然后是 p x v x m
Matrix.multiplyMM(mvpMatrix, 0, projectionMatrix, 0, mvpMatrix, 0)
val u_Matrix = getUniform("u_Matrix")
GLES30.glUniformMatrix4fv(u_Matrix, 1, false, mvpMatrix, 0)
//useVaoVboAndEbo
texture?.apply {
GLES30.glBindTexture(GLES30.GL_TEXTURE_2D, id)
}
//GLES30.glDrawElements(GLES30.GL_TRIANGLE_STRIP, 6, GLES30.GL_UNSIGNED_INT, 0)
GLES30.glDrawArrays(GLES30.GL_TRIANGLES, 0, 36)
}
效果:

参考:
https://learnopengl-cn.github.io/01%20Getting%20started/08%20Coordinate%20Systems/