MATLB|电动汽车充放电的最优调度

news2024/11/24 0:24:24

目录

一、概述

二、电动汽车

2.1 电动汽车的类型

2.2电动汽车行程开始时间

2.3 电动汽车行驶里程

三、Matlab实现

3.1 代码前的准备

3.2 运行结果

 四、往期回顾

五、Matlab代码实现

 

一、概述

电动汽车能够良好发展离不开精确的电动汽车充电负荷预测,目前,大多数充电负荷预测研究都基于蒙特卡洛模拟算法来计算。其中,文献[13]将电动汽车分为私家车、公交车和出租车三种类型进行分析建模,但是对于车辆的起始荷电状态和起始充电时间分布的选取存在一定的主观性。文献[14]利用了统计学的方法建立了行程结束时间和日行驶里程的概率分布模型,并认为行程结束时间等于起始充电时间,但对于日充电频率大于1次的电动汽车来说并不合理。文献[15]考虑了电动汽车每天的行驶里程及电池容量,但充电起始时间的确定也不准确。综上所述,目前的研究考虑因素不够全面,导致预测不够准确,例如:1)未考虑到电动汽车的出行轨迹分布;2)未考虑到电动汽车充电场所的不确定性。

二、电动汽车

对于电动汽车的负荷来说,影响因素从来都不是单一的,是多种因素共同影响。其大小和出行轨迹分布也由多种情况来左右,比如电动汽车的性能是否优良、汽车用户的使用方式是否合适、电动汽车充电的环境是否适合以及电动汽车的行驶路面是否平坦等。如果想进一步精确预测电动汽车充电负荷的出行轨迹分布,需要对以下几个可能影响因素进行深度考虑:电动汽车的种类、电动汽车行程开始时间电动汽车行驶里程﹑停驻时间、充电方式等。

2.1 电动汽车的类型

当前中国的电动汽车广泛应用的地方主要有三种:私家车、出租车、公交车,公交车基本按照计划的轨迹及时间点来行驶,出行轨迹及时间相对固定,所以其充电的场所确定较为简单;私家车和出租车由于出行轨迹复杂且出行时间具有不确定性充电场所的确定存在难度。因此,充电负荷的场所及大小会因为电动汽车类型的不同显示出一些差异性。

2.2电动汽车行程开始时间

对电动汽车来说,每天的使用时间及需要充电的时间分布上显然存在密切的联系,本文使用某调查的统计结果,从中调出某私家车一天内的行程开始时间来研究电动汽车的运行特性。
利用实际数据,可以得到电动私家车行程开始时间的概率分布。用户行程开始时间概率分布如图1所示。

              

对该概率分布进行拟合,发现用户行程开始时间的概率近似服从正态分布其概率密度函数为：

                

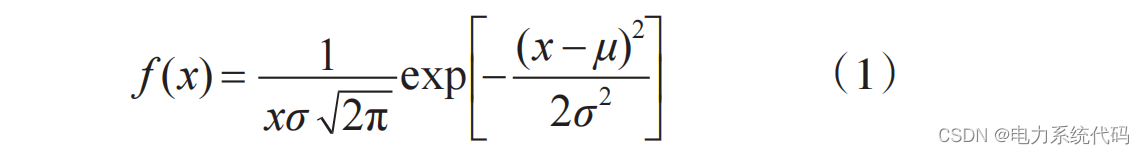
其中，\mu是行程开始时间的期望值,\sigma是标准差。拟合后求得\mu =7.89,\sigma=1.96。

2.3 电动汽车行驶里程

电动汽车使用者对电动汽车的充电频次和时间都与其日出行里程数有着密不可分的各种联系。日出行里程数也会因为不同使用者存在差异，主要是因为各电动汽车使用者的使用习惯不同,对私家车来说,主要用于上下班和休闲娱乐途中,行驶里程短且较为规律。

根据2017年NHTS得出的结果来看,电动私家车的每段行驶里程数趋向于对数正态分布,其概密度函数为：

      

其中,\mu是行程距离的期望值,\sigma是标准差。拟合后求得\mu =3.68,\sigma =0.88。 

 出租车每日的行驶里程数大约为300km，为三者中行驶里程数最长的车型；公交车比出租每日行

驶里程数相对少一些，约为200km。

三、Matlab实现

3.1 代码前的准备

安装CVX包：

先点击这里：风电随机性动态经济调度模型

然后：也是代码前的准备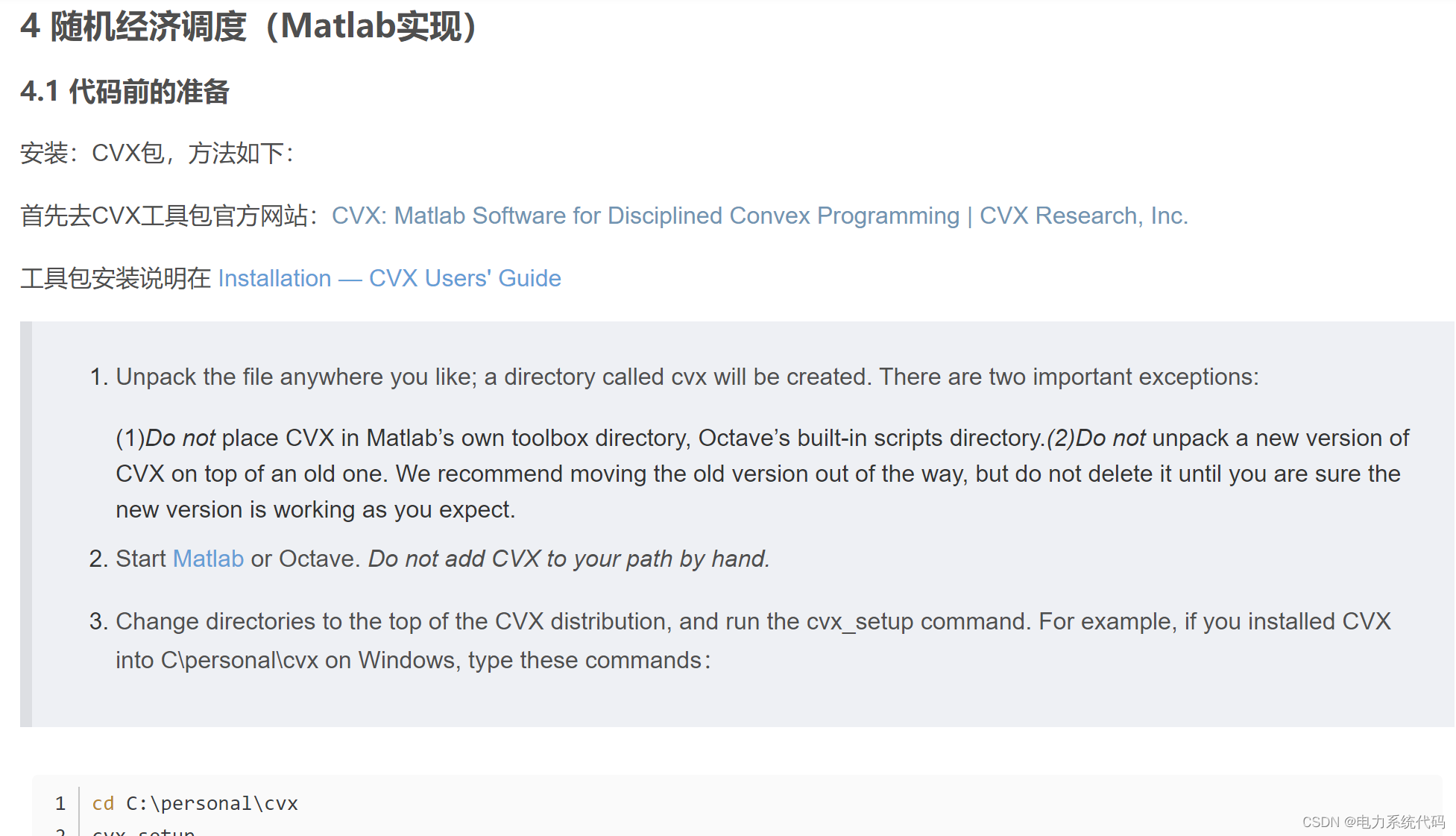

本文是一种最优调度算法，以最大限度地降低电动汽车充放电的总成本。

部分代码：

close all;
clc;
clear;


%% 参数设置

%==(1)基本荷荷向量===
L_b=[
    1648181.19
    1510114.92
    1404600.51
    1348140.62
    1355294.53
    1380434.41
    1472398.73
    1619859.88
    1774726.71
    1891739.09
    2024589.36
    2154006.65
    2214969.44
    2248348.3
    2257444.05
    2253898.58
    2251095.52
    2240891.11
    2187658.11
    2060455.55
    2032531.95
    1984614.47
    1846244.76
    1676395.15];

%====(2)预测的基本负荷（平均相对误差 = 0.089）====
P_L_b1=[
    1737223.863
    1603267.075
    1501043.33
    1434323.708
    1427034.265
    1445808.13
    1535646.84
    1703557
    1878913.403
    2041190.428
    2189203.243
    2300813.958
    2376838.56
    2431838.998
    2456820.033
    2472628.88
    2497750.498
    2502256.753
    2487853.418
    2333072.535
    2313458.498
    2278059.543
    2121749.573
    1908084.005];


%====(3)预测的基本负荷（平均相对误差 = 0.0414）====
P_L_b2=[
    1599948.91
    1468345.518
    1370502.199
    1310946.046
    1308525.559
    1330298.288
    1417044.254
    1592177.276
    1774327.31
    1935791.394
    2081450.673
    2194127.508
    2266347.528
    2310264.895
    2317806.969
    2328853.886
    2350763.395
    2356239.943
    2340220.599
    2215920.234
    2192252.838
    2168526.739
    2014122.374
    1803843.804];

%=====(4)第二次预测的基本负荷（更好的预测）（平均相对误差=0.0234）===
P_L_b3=[
    1648037.519
    1458944.669
    1366366.043
    1310276.476
    1309105.99
    1329282.055
    1411672.493
    1587762.671
    1728429.463
    1888917.875
    2032770.183
    2133804.711
    2199858.463
    2240117.111
    2241852.165
    2245048.574
    2259487.69
    2260142.395
    2243557.341
    2145562.018
    2122157.145
    2104126.554
    1948760.596
    1740961.875];

%=====选择使用哪个预测负荷====
P_L_b=P_L_b2;

%% 微电网的基本负荷
Scale_factor=1/1500;
L_b_mic=L_b*Scale_factor;  % 基本负荷
P_L_b_mic=P_L_b*Scale_factor;  % 基本预测负荷

%% 价格模型
% alfa=1.0;
% theta=1;
omega=1.2*max(L_b_mic);
k_0=0.0001;
k_1=0.00012;
k_2=0;
%====(1)寿命缩减成本======
beta=0.001;
beta=0;

%===简单乘法计算=====
% k_con=alfa/(omega^theta*(theta+1));

%=====充电间隔时间======
tau=1; % 小时内

%=====充电间隔数========
num_slot=length(L_b_mic);

%====(2)基本价格=======
price_basic=zeros(num_slot,1); % 基于基本负荷的价格
for i=1:num_slot
    price_basic(i)=k_0+k_1* L_b_mic(i);
end
fprintf('价格，最低价格=%g,最高价格=%g.\n',min(price_basic), max(price_basic));


%% 电动汽车EV容量
Cap_battery_org=16; % KWh
gamma=0.9; % 充电完成时电池的百分比
Cap_battery=gamma*Cap_battery_org;

%% ==最大充电率===
P_max=5; % KW

%% 电动汽车数量
num_EV=200;

% 仅给电池充电的电动汽车的百分比
P_Chg=0;

% CHG EVs数量
num_CHG_EV=round(P_Chg*num_EV);  % CHG EV 将位于 EV 信息矩阵的前面部分。
% V2G EVs数量
num_V2G_EV=num_EV-num_CHG_EV;

%% 电动汽车充电模式
% 30% 的电动汽车在间隔 1 之前连接到充电站，其余的均匀分布

%EV矩阵：1) 到达时间，2) 出发时间，3) 初始能量，4) 充电周期，5) 最小充电时间%

% EV_info=zeros(num_EV,3);
%===间隔1前接入站的EVS百分比====
% Per_EV=0.1;
%=====其他车辆到达时间均匀分布在[  1,20 ]之间======
% for i=1:num_EV
%     temp_00=rand;
%     if temp_00<=Per_EV
%         T_arrival(i,1)=1;
%     else
%         T_arrival(i,1)=round(1 + (20-1).*rand);
%     end
% end
%
%=====充电时间均匀分布在 [4, 12] 小时之间======
% T_charging= round(4 + (12-4).*rand(num_EV,1));
% T_charging=-1*sort(-1*T_charging);
%
% % the departure time
% for i=1:num_EV
%     T_departure(i,1)=min(24, T_arrival(i,1)+T_charging(i,1));
% end
%====初始电量均匀分布在电池容量的[0 0.8]之间======
% Ini_percentage=0+ (0.8-0).*rand(num_EV,1);
% % fill the EV_info
% EV_info(:,1)=T_arrival;
% EV_info(:,2)=T_departure;
% EV_info(:,3)=Cap_battery_org*Ini_percentage;
%
% for i=1:num_EV
%     EV_info(i,4)=EV_info(i,2)-EV_info(i,1)+1; % 充电周期
%     EV_info(i,5)=EV_info(i,3)/P_max; % 最小充电时间
%     if EV_info(i,4) < EV_info(i,5)
%         fprintf('EV %g 充电时间不合理.\n',i);
%     end
% end
%
% % save and load EV_info
% save EV_info.txt EV_info -ascii;

load EV_info.txt;
EV_info=EV_info(1:num_EV,:);

%% 电动汽车与充电间隔的关系
F=zeros(num_EV, num_slot);
G=ones(num_EV, num_slot);
for i=1:num_EV
    for j=EV_info(i,1):EV_info(i,2)
        F(i,j)=1;
        G(i,j)=0;
    end
end
F1=reshape(F',1,[]);
% F=ones(num_EV, num_slot);

%% 绘制基本负荷
xx_1=1:num_slot;
figure;
yy_1(:,1)=L_b_mic;
yy_1(:,2)=P_L_b_mic;
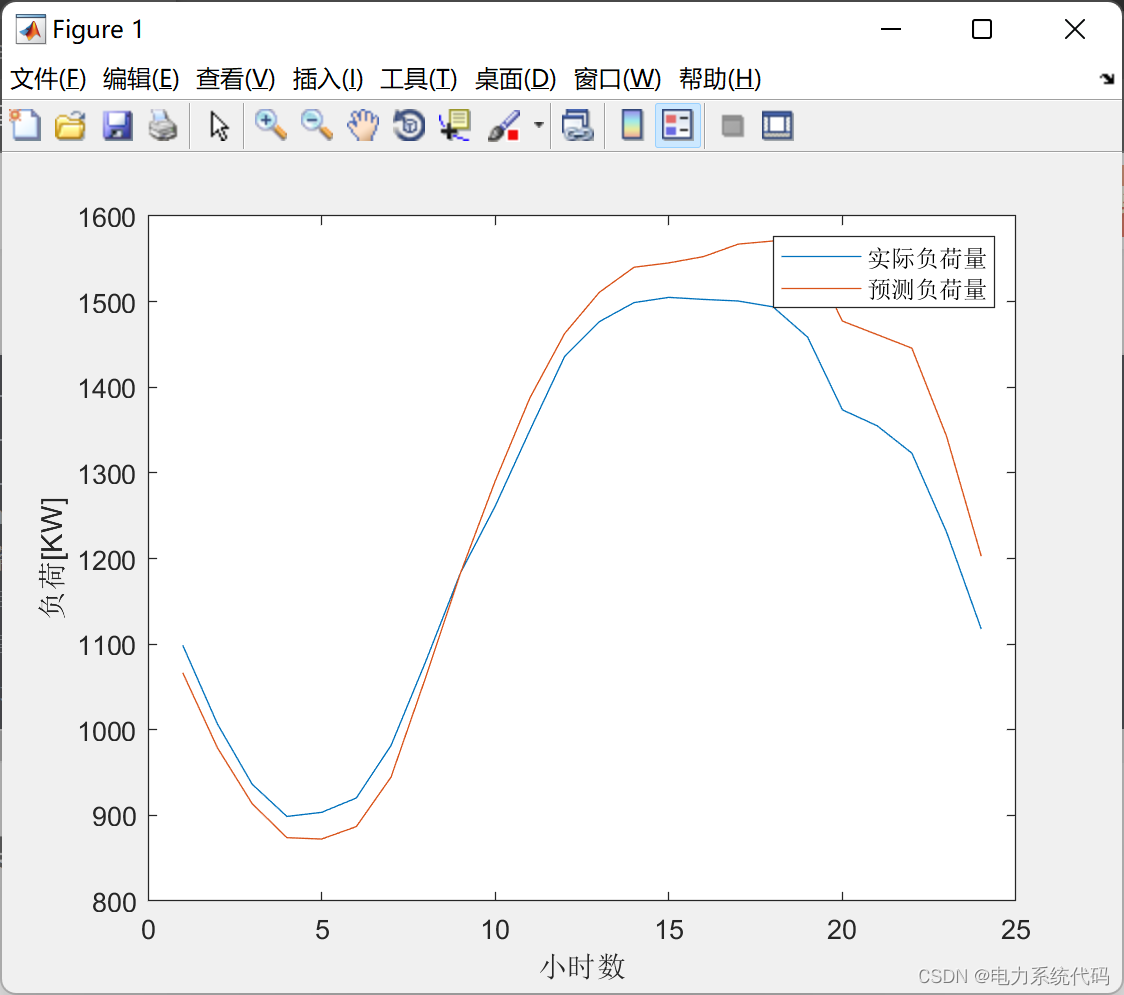
plot(xx_1,yy_1);
ylabel('负荷[KW]');
xlabel('小时数');
legend('实际负荷量','预测负荷量');

%% 使用CVX工具的V2G全局最优方案

%（1）等式约束: Ax=b
% （2）优化变量x=[z1, z2, ..., z_24, x11, x12, ...., x_100,24]'
num_OptVar=1*num_slot+num_slot*num_EV;
b_a=L_b_mic; %第一个等式约束的矩阵
A1_a=zeros(num_slot, num_OptVar-1*num_slot);
A1=[eye(num_slot) A1_a];

A2_a=zeros(num_slot, num_OptVar-1*num_slot);
s_temp=0;
for i=1:num_slot
    for j=1:num_EV
        A2_a(i, (j-1)*num_slot+i)=F(j,i);
        % fprintf('Assign F(%g,%g)=%g, to A2_a(%g, %g).\n',j,i,F(j,i),i,(j-1)*num_slot+1);
        s_temp=s_temp+F(j,i);
    end
end
A2_b=zeros(num_slot, num_slot);
A2=[A2_b A2_a];

A_a=A1-A2;  % 第一个等式约束的矩阵
clear A1 A2 A1_a A2_a A2_b;

%======第一个等式约束的矩阵=====
B_1=zeros(num_EV, num_OptVar-1*num_slot);
for i=1:num_EV
    B_1(i,(i-1)*num_slot+1:(i-1)*num_slot+num_slot)=F(i,:);
end
temp_1=zeros(num_EV, num_slot);
B1=[temp_1 B_1];    % 第二等式约束的矩阵
b_b=(Cap_battery/tau)*ones(num_EV,1)-EV_info(:,3);% 第二等式约束的矩阵
clear  B_1  temp_1;

%合并等式矩阵
% Eq_left=[A_a' B1']';
% Eq_right=[b_a' b_b']';


%% ======等式约束=====
Eq_L=A_a;
Eq_R=b_a;
clear  A_a  b_a;
%% ======不等式约束=====
% ====1)第一个不等式约束=====
In_1=zeros(num_EV*num_slot, num_OptVar);
for i=1:num_slot
    for j=1:num_EV
        In_1((i-1)*num_EV+j,num_slot+(j-1)*num_slot+1:num_slot+(j-1)*num_slot+i)=F(j,1:i);
        %         fprintf('set row %g, col %g:%g by using F(%g,1:%g).\n',(i-1)*num_EV+j,num_slot+(j-1)*num_slot+1,num_slot+(j-1)*num_slot+i,j,i);
    end
end
In_1=-1*In_1;  % 第一个不等式，左边
In_b1=zeros(num_EV*num_slot, 1);    % 第一个不等式，右边, [EV1_slot1, EV2_slot1, ..., EV1_slot2, EV2_slot2,...]'
for i=1:num_slot
    In_b1( (i-1)*num_EV+1:(i-1)*num_EV+num_EV, 1 )= (1/tau)*EV_info(1:num_EV,3);
end

%=====2)第二个不等式约束=====
In_2=-1*In_1; %第二个不等式约束，左边
In_b2=zeros(num_EV*num_slot, 1);    % 第二个不等式约束，右边, [EV1_slot1, EV2_slot1, ..., EV1_slot2, EV2_slot2,...]'
temp_b2=Cap_battery_org - EV_info(1:num_EV,3);
for i=1:num_slot
    In_b2( (i-1)*num_EV+1:(i-1)*num_EV+num_EV, 1 )= (1/tau)*temp_b2;

''''''''''''

% 绘出每个电动车(全局最优方案)的电能水平演化图。
figure;
xxx=0:num_slot;
plot(xxx,v_Energy_variation(1:40,:));
ylabel('电能[KWH]');
xlabel('小时数');
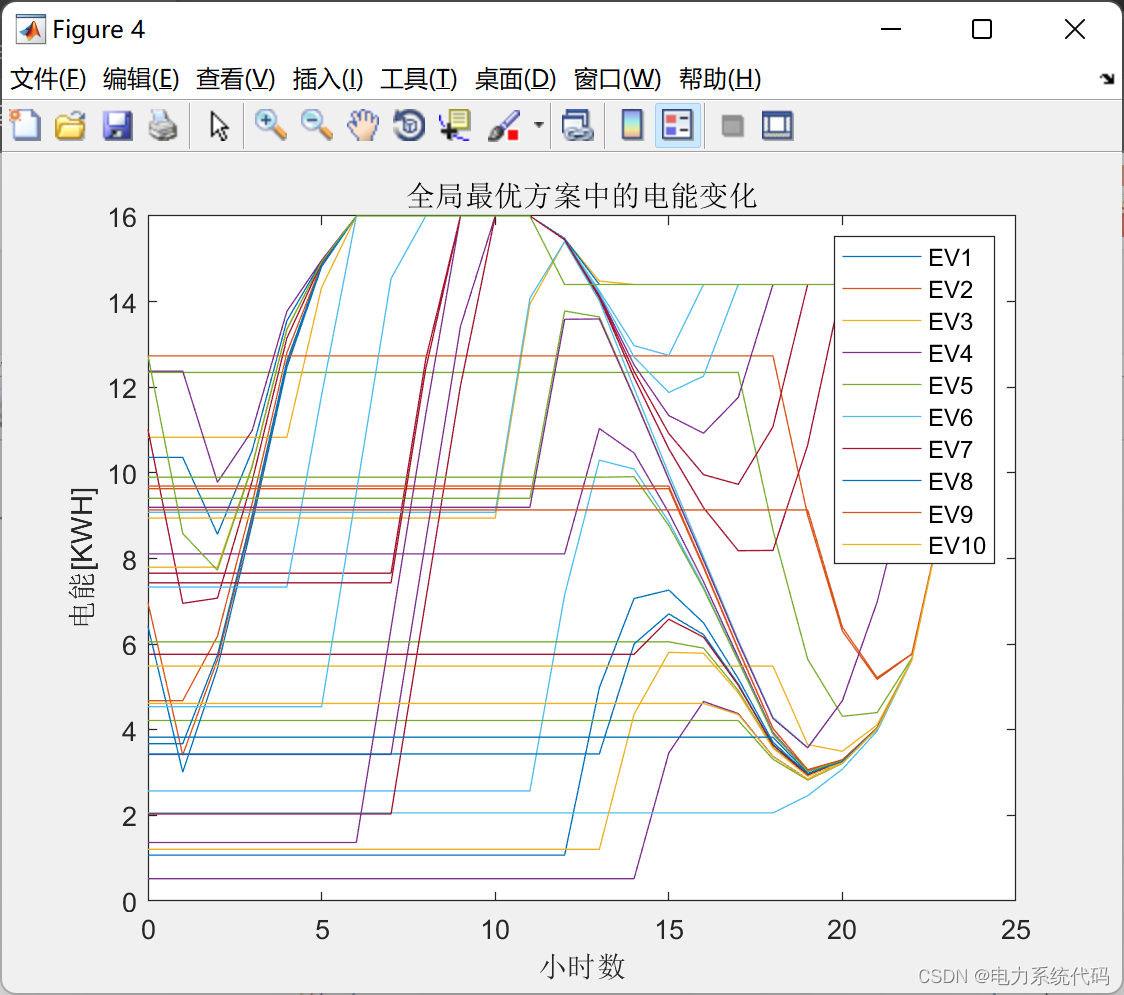
legend('EV1','EV2','EV3','EV4','EV5','EV6','EV7','EV8','EV9','EV10');
title('全局最优方案中的电能变化');

% 绘制每个电动汽车的能量水平演化(局部最优方案)
figure;
xxx=0:num_slot;
plot(xxx,Energy_variation);
ylabel('电能[KWH]');
xlabel('小时数');
legend('EV1','EV2','EV3','EV4','EV5','EV6','EV7','EV8','EV9','EV10');
title('局部最优方案中的电能变化');

% 绘制每个EV的能量水平演化(等分配方案)
figure;
plot(xxx,N_Energy_variation);
ylabel('电能[KWH]');
xlabel('小时数');
legend('EV1','EV2','EV3','EV4','EV5','EV6','EV7','EV8','EV9','EV10');
title('均等分配最优方案中的电能变化');

% %绘制每辆电动汽车的充电率
figure;
EV_ID=65;
energy_mmm(1,:)=v_Energy_variation(EV_ID,:);
energy_mmm(2,:)=Energy_variation(EV_ID,:);
energy_mmm(3,:)=N_Energy_variation(EV_ID,:);
plot(xxx,energy_mmm);
ylabel('电能 [KWH]');
xlabel('时间(Hours)');
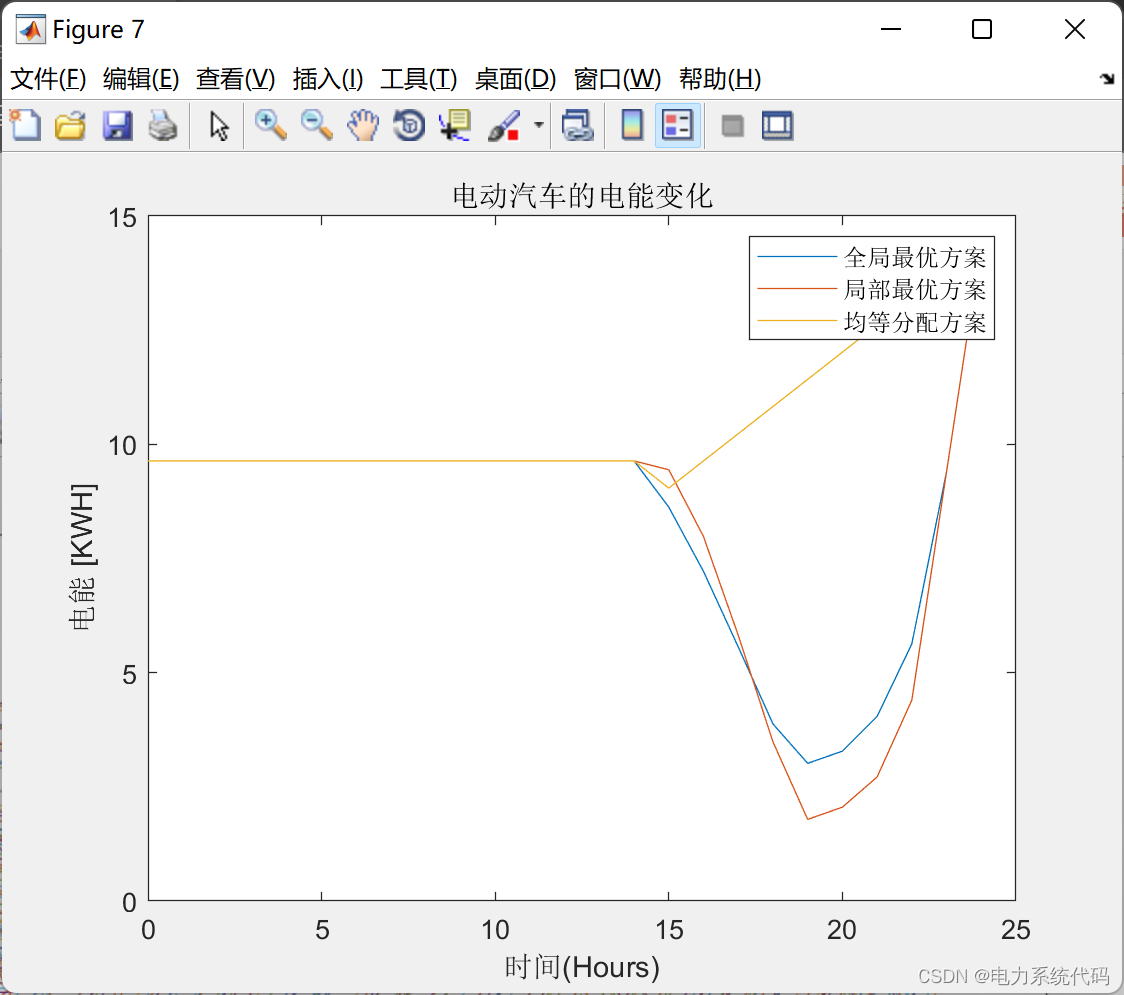
legend('全局最优方案','局部最优方案','均等分配方案');
title('电动汽车的电能变化');

figure;
nnn(:,1)=v_x_Matrix(EV_ID,:)';%全局最优
nnn(:,2)=x_Matrix(EV_ID,:)';%局部最优
nnn(:,3)=N_x_Matrix(EV_ID,:)';%均等分配
h=bar(xx,nnn);
ylabel('速率[KW]');
xlabel('时间(Hours)');
legend('全局最优','局部最优','均等分配');
title('全局最优方案中的充放电速率');

3.2 运行结果




 

 

 

 

 四、往期回顾

模拟大规模电动车充电行为（Matlab实现）

电动汽车对系统运行的影响（Matlab实现）

基于蒙特卡洛法的规模化电动汽车充电负荷预测（Python&Matlab实现）

基于电动汽车的带时间窗的路径优化(Python&Matlab代码实现）

（Matlab实现）基于蒙特卡诺和拉格朗日乘子法的电动车调度【有序、无序充放电】

五、Matlab代码实现

回复：电动汽车充放电的最优调度

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/91473.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

2022全年度烘干机十大热门品牌销量榜单

2022全年度烘干机十大热门品牌销量榜单

在“宅经济”时代&#xff0c;人们对大家电的需求持续高速增长。在当前的大环境下&#xff0c;人们的健康意识在不断提高&#xff0c;拥有除菌防菌功能的烘干机也更受欢迎。因此&#xff0c;烘干机作为快速进入普及阶段的家电新品&#xff0c;市场增长空间非常大。 根据鲸参谋数…
阅读更多...
RCE绕过靶场练习

RCE绕过靶场练习

目录 CTF-01 CTF-02 CTF-03 CTF-04 CTF-05 CTF-01 测试回显 Array ([0] > PING 127.0.0.1 (127.0.0.1): 56 data bytes[1] > 64 bytes from 127.0.0.1: seq0 ttl42 time0.028 ms[2] > 64 bytes from 127.0.0.1: seq1 ttl42 time0.059 ms[3] > 64 bytes from …
阅读更多...
Javascript 面向对象的缺陷，父类能调用被子类重写后的方法

Javascript 面向对象的缺陷，父类能调用被子类重写后的方法

问题背景 前些天做项目练手时&#xff0c;遇到一个需要写类的场景&#xff0c;各个类之间的交互我打算用事件的方式进行&#xff0c;就自然地在父类继承了EventEmitter类。然后在父类对一个具体事件注册了一个默认监听&#xff0c;子类通过注册自己专有的监听细化逻辑。代码逻…
阅读更多...
win7、win10关闭驱动签名，进入驱动测试模式，以及常见初级问题的解决

win7、win10关闭驱动签名，进入驱动测试模式，以及常见初级问题的解决

win7关闭驱动签名&#xff0c;进入驱动测试模式win7、win10关闭驱动签名、进入驱动测试模式DebugView工具运行提示"Dbgv.sys: 拒绝访问"驱动项目配置属性常用设置驱动中KdPrint打印UNICODE_STRING字符串常用方法没使用的变量在编译时报警告&#xff1a;未引用的形参错…
阅读更多...
文字转语音真人发声软件哪个好？这些实用软件快来收好

文字转语音真人发声软件哪个好？这些实用软件快来收好

平时大家结束了一天的工作&#xff0c;会不会在空闲时间好好放松一下呢&#xff1f;如果是坐公交车或者地铁的小伙伴&#xff0c;想要在下班途中看一些电子书籍或者新闻&#xff0c;却因为下班高峰期人潮拥挤&#xff0c;导致无法腾出手来阅读&#xff0c;这时候你们会怎么解决…
阅读更多...
红队基础知识

红队基础知识

文章目录红队前置准备网络攻击链工程和操作攻击性思维渗透测试漏洞研究软件开发基础设施网络和系统逆向工程社会工程学物理安全威胁情报安全事件的检测和响应技术写作培训与汇报总结红队前置准备 红队通常指在对抗情况下需要仿真、模拟或以其他方式扮演某个、某组入侵者或理论…
阅读更多...
【Docker】（一）基本概念与安装使用

【Docker】（一）基本概念与安装使用

1.概述 最近学习了Docker的使用&#xff0c;想通过一个系列的笔记来记录学习的过程与收获&#xff0c;并为以后的生产工作提供指导。 我一直认为学习一门技术时&#xff0c;需要先了解这门技术的基本概念&#xff0c;了解它能解决的问题&#xff0c;这样才能定位明确的学习目标…
阅读更多...
frp内网穿透https

frp内网穿透https

在公网服务器搭建frps(service)&#xff0c;在内网本地机子搭建frpc(client)&#xff0c;流量通过访问公网ip&#xff0c;经过frps服务端转发到fprc客户端&#xff0c;fprc再转发到本地web应用。 官方下载地址​ https://github.com/fatedier/frp/releases 官方文档地址https…
阅读更多...
智能门锁“激战正酣”

智能门锁“激战正酣”

近年来&#xff0c;智能化已经成为了高频词&#xff0c;越来越多的行业都在朝着智能化方向发展&#xff0c;家居行业也不例外。受技术升级、居民收入水平提高等多重因素影响&#xff0c;整个智能家居行业呈现出了蓬勃发展态势。据亿欧智库预测&#xff0c;2025年中国智能家居市…
阅读更多...
客运车票网站

客运车票网站

开发工具(eclipse/idea/vscode等)&#xff1a; 数据库(sqlite/mysql/sqlserver等)&#xff1a; 功能模块(请用文字描述&#xff0c;至少200字)&#xff1a; 题目&#xff1a;基于Wb的公路客运车票信息管理系统设计与实现 时了解客运站动态。 角色&#xff1a;乘客、管理员 (2)车…
阅读更多...
[附源码]Node.js计算机毕业设计-高校人事管理系统Express

[附源码]Node.js计算机毕业设计-高校人事管理系统Express

项目运行 环境配置&#xff1a; Node.js最新版 Vscode Mysql5.7 HBuilderXNavicat11Vue。 项目技术&#xff1a; Express框架 Node.js Vue 等等组成&#xff0c;B/S模式 Vscode管理前后端分离等等。 环境需要 1.运行环境&#xff1a;最好是Nodejs最新版&#xff0c;我…
阅读更多...
C++设计模式的个人理解 繁琐的底层需要合理设计

C++设计模式的个人理解 繁琐的底层需要合理设计

一、为什么会有设计模式 由于每个人自身的能力、所在的层次、看问题的角度都不同&#xff0c;仅凭直觉“对现实建模”&#xff0c;很有可能会生成一些大小不均、职责不清、关系混乱的对象&#xff0c;最后搭建出一个虽然可以运行&#xff0c;但却难以理解、难以维护的系统。为此…
阅读更多...
基于Java+Mysql实现酒店预订系统【100010045】

基于Java+Mysql实现酒店预订系统【100010045】

酒店预订系统 1.引言 1.1编制目的 1.详细完成对酒店预订系统的概要设计&#xff0c; 2.达到指导详细设计和开发的目的&#xff0c; 3.同时实现和测试人员及用户的沟通。 3.本报告面向开发人员&#xff0c;测试人员及最终用户的编写额&#xff0c;是了解系统的导航。 1.2…
阅读更多...
Flink基本转换算子

Flink基本转换算子

文章目录1.映射&#xff08;map&#xff09;2.过滤&#xff08;filter&#xff09;3.扁平映射&#xff08;flatMap&#xff09;4.按键分区&#xff08;keyBy&#xff09;5. 简单聚合&#xff08;sum&#xff0c;min&#xff0c;max等&#xff09;6.归约聚合&#xff08;reduce&…
阅读更多...
m基于LDPC+QPSK通信链路误码率matlab仿真

m基于LDPC+QPSK通信链路误码率matlab仿真

目录 1.算法描述 2.仿真效果预览 3.MATLAB核心程序 4.完整MATLAB 1.算法描述 LDPC ( Low-density Parity-check&#xff0c;低密度奇偶校验&#xff09;码是由 Gallager 在1963 年提出的一类具有稀疏校验矩阵的线性分组码 (linear block codes)&#xff0c;然而在接下来的 …
阅读更多...
第五届“强网”拟态防御国际精英挑战赛在南京举行——开辟网络安全新赛道 引领网络弹性新优势

第五届“强网”拟态防御国际精英挑战赛在南京举行——开辟网络安全新赛道 引领网络弹性新优势

12月15日&#xff0c;第五届“强网”拟态防御国际精英挑战赛在南京紫金山实验室隆重开幕&#xff0c;来自国内外60支顶尖战队将通过云上和线下相结合的方式展开72小时的高强度对抗。大赛组委会主席、紫金山实验室首席科学家、中国工程院邬江兴院士指出&#xff0c;本届挑战赛瞄…
阅读更多...
jvm内存模型+类加载机制+垃圾手机器

jvm内存模型+类加载机制+垃圾手机器

1、类加载器分类 1、引导类加载器&#xff0c;负责加载支撑Jre/lib目录下的核心类库 2、扩展类加载器&#xff1a;负责加载Jre/lib目录下的ext扩展类jar包 3、应用程序类加载器&#xff1a;负责加载classpath下的类包 4、自定义类加载器&#xff1a;负责加载用户自定义路径下的…
阅读更多...
值得思索的：ArrayList和线性表，你确定错过这次机会

值得思索的：ArrayList和线性表，你确定错过这次机会

线性表&#xff1a; 线性表&#xff08;linear list&#xff09;是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结 构&#xff0c;常见的线性表&#xff1a;顺序表、链表、栈、队列... 线性表在逻辑上是线性结构&#xff0c;也就说是连续的一条…
阅读更多...
Go项目实战:01-聊天室+map竞争需要上锁

Go项目实战:01-聊天室+map竞争需要上锁

实现一个聊天室&#xff08;群&#xff09;&#xff1a; 功能分析&#xff1a; 1、上线下线2、聊天&#xff1a;其他人和自己都可以看到聊天消息3、查询当前的聊天室用户所有人的名字4、可以修改自己的名字5、超时潜水踢出机制 技术点分析&#xff1a; 1、socket tcp编程2、…
阅读更多...
Adam算法及python实现

Adam算法及python实现

文章目录算法介绍代码实现结果展示参考算法介绍 Adam算法的发展经历了&#xff1a;SGD->SGDM->SGDNA->AdaGrad->AdaDelta->Adam->Adamax的过程。它是神经网络优化中的常用算法&#xff0c;在收敛速度上比较快&#xff0c;比SGD对收敛速度的纠结上有了很大的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023