1.深度学习基础知识
1.1 数据操作
1.1.1 数据结构
机器学习和神经网络的主要数据结构,例如
0维:叫标量,代表一个类别,如1.0
1维:代表一个特征向量。如 [1.0,2,7,3.4]
2维:就是矩阵,一个样本-特征矩阵,如: [[1.0,2,7,3.4 ]
[2.0,3,7,4.4 ] ],每一行是样本,每一列是特征;

3维:RGB图片(宽(列)x高(行)x通道) 三维数组,[[[ 1.0,2,7,3.4 ]
[2.0,3,7,4.4 ] ]
[[2.0,3,7,4.4 ]]]
4维:N个三维数组放在一起,如一个RGB图片的批量(批量大小x宽x高x通道)
5维:一个视频的批量(批量大小x时间x宽x高x通道)

1.1.2 创建数组
创建数组需要如下:
- 形状:例如3x4d矩阵
- 每个元素的数据类型:例如32位符点数
- 每个元素的值:例如全是0,或者随机数
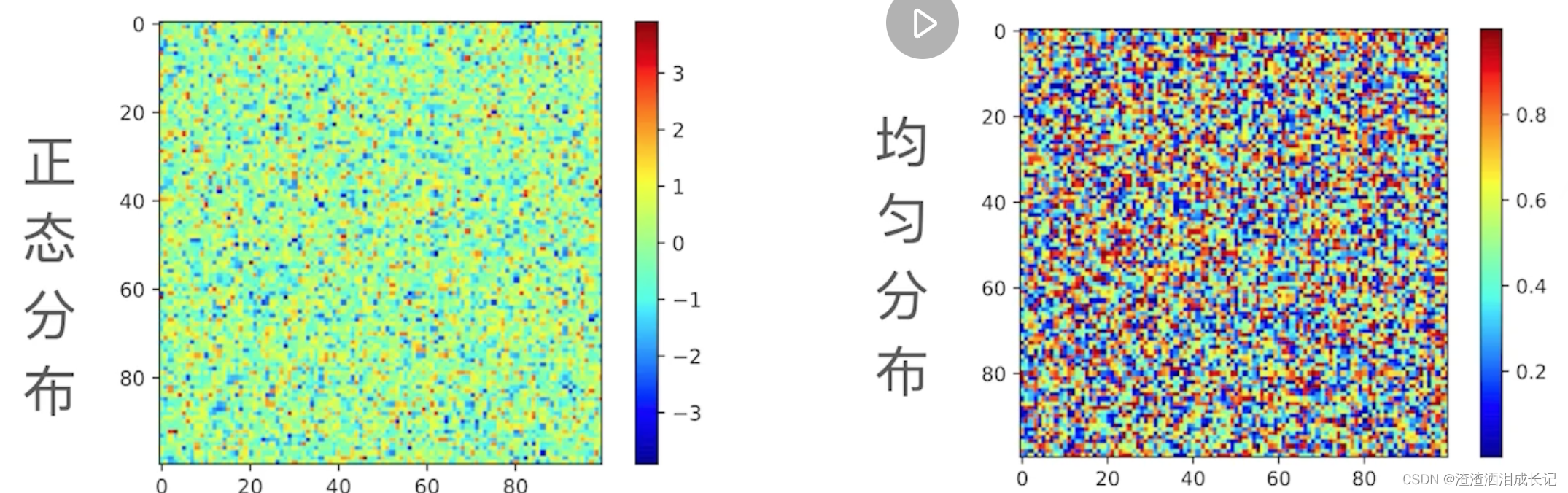
访问数组
[1,:] 访问第一行的所有列。
[:,1]访问第一列把所有行查询出来
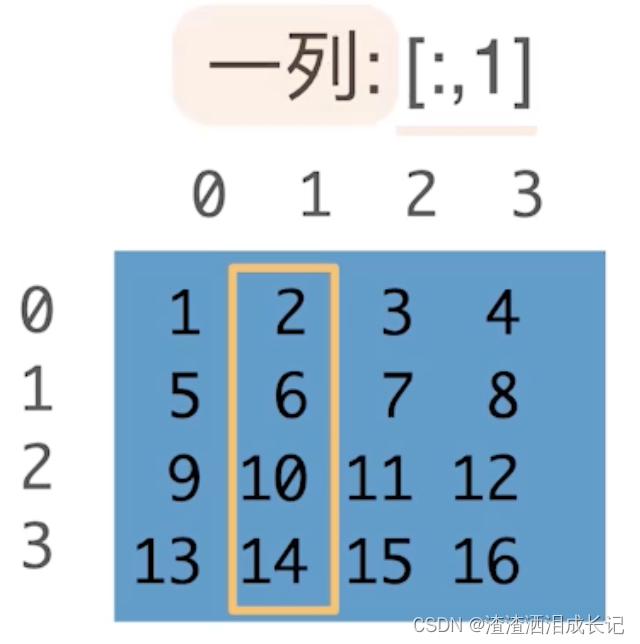
子区域:[1:3,1:] 代表访问1-2行的数据,虽然是3但是3是开区间,然后列是从第一列到最后都查询,因为是:嘛。
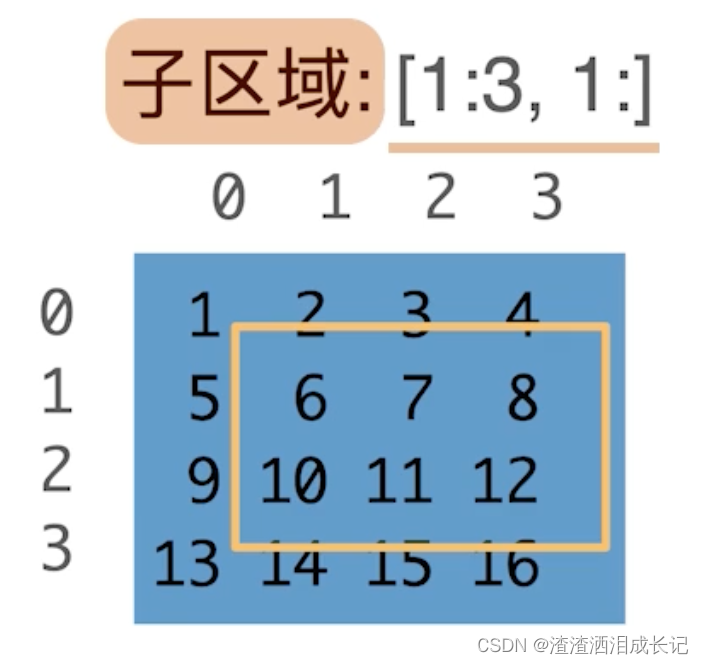
子区域:[::3,::2]访问一个带跳转的子区域,行里每三行眺一行,列里每两行眺一行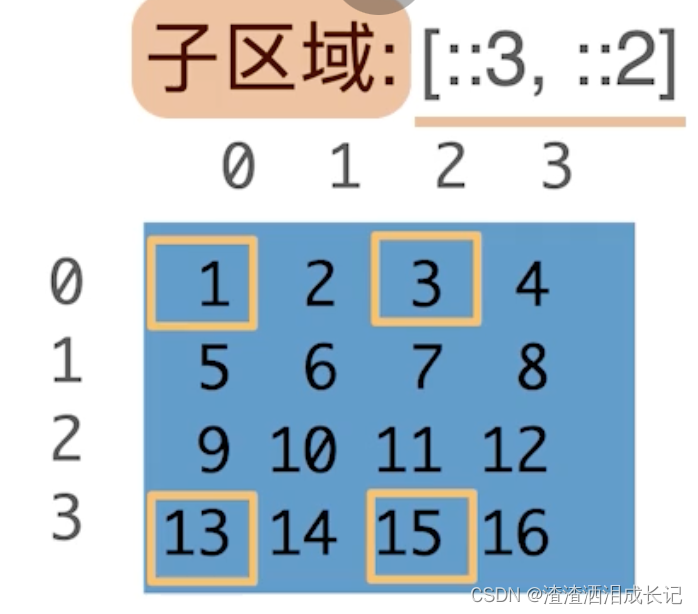
1.2 数据操作实现
!pip install torch
import torch
x=torch.arange(12)
print(x)结果:
tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
返回的是一个张量,调用arange给12则把0-12之前的数字拿出来。
张量:是一种多维矩阵,是神经网络的基本数据结构。它的概念源于数学,具有最多八个维度。它是一种应用于机器学习,深度学习和其他人工智能应用的非常有用的数据结构。
张量可以被认为是子元素的多维数组。该子元素可以是实数、向量、矩阵或任何其他多维类型。张量提供了一种统一的方式来处理复杂的数据结构。而且,它的可视化表示也更加直观,清晰。
这意味着,当程序在计算机中运行时,它可以将各种类型的数据,比如图片、文本、语音等,组织成多维数组的组成部分。张量通常被用于吃进、学习和转换复杂的结构化输入(如图像)并进行预测。有了张量,程序可以更自由地传输和处理复杂数据,从而更快、更准确地开展预测。
我们可以通过张量的shape数学来访问张量的形状和张量中元素的总数。
x.shapetorch.Size([12])
# 元素总数
x.numel()12
要改变一个张量的形状不改变元素数量和元素值,我们可以调用rehape函数。
# 将之前的标量数据转换为3x4矩阵
x=x.reshape(3,4)
print(x)
创建一个指定形状的全零张量(tensor)和全一张量。它接受一个或多个整数作为参数,表示张量的形状。
y = torch.zeros((2, 3, 4)) # 创建一个形状为(2,3,4)的张量,其中所有元素都设置为0,第一个参数代表创建几个3行4列的矩阵
print(y)
z = torch.ones((2, 3, 4)) # 创建一个形状为(2,3,4)的张量,其中所有元素都设置为1,第一个参数代表创建几个3行4列的矩阵
print(z)

通过提供包含数值的Python列表(或嵌套列表),来为所需张量中的每个元素赋予确定值。
b=torch.tensor([[2,1,4,3],[1,2,3,4]])
print(b)
# 打印形状
print(b.shape)
可以在同一形状的任意两个张量上调用按元素操作加减乘除、幂运算等等
x=torch.tensor([1.0,2,4,8])
y=torch.tensor([2,2,2,2])
print(x+y)
print(x-y)
print(x*y)
print(x/y)
print(x**y) #**运算符是求幂运算,对每个x元素求二次方
# 给x每个元素做指数运算
print(torch.exp(x))tensor([ 3., 4., 6., 10.])
tensor([-1., 0., 2., 6.])
tensor([ 2., 4., 8., 16.])
tensor([0.5000, 1.0000, 2.0000, 4.0000])
tensor([ 1., 4., 16., 64.])
tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
可以把多个张量连结在一起, 把它们端对端地叠起来形成一个更大的张量
x=torch.arange(12,dtype=torch.float32).reshape((3,4))
y=torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
print("x:",x)
print("y:",y)
print("xy组合按行:",torch.cat((x,y),dim=0))#按行连结两个矩阵
print("xy组合按列:",torch.cat((x,y),dim=1))#按列连结两个矩阵
也可以通过逻辑运算符构建二元张量
x==y
对张量中的所有元素进行求和,会产生一个元素的张量
print(x.sum())tensor(66.)
即使形状不同,我们仍然可以调用广播机制来执行按元素操作 。但是维度需相同,就像下面都是2维
a=torch.arange(3).reshape((3,1))
b=torch.arange(2).reshape((1,2))
print("a:",a)
print("b:",b)
print(a+b)执行完结果如下:其实将a里的列复制成和b对应的列一致,b要复制成行与a的一致,然后相加即可
∫a: tensor([[0],
[1],
[2]])
# 相当于复制成
# tensor([[0, 0],
# [1, 1],
# [2, 2]])
b: tensor([[0, 1]])
tensor([[0, 1],
[1, 2],
[2, 3]])
# tensor([[0, 1], [0, 1], [0, 1]])我们来取元素数据,
# -1取出最后一个元素
print(x[-1])
# [1:3]取出第二个和第三个元素
print(x[1:3])原本的 x数据如下:
x: tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]])取出数据结果如下:
tensor([ 8., 9., 10., 11.])
tensor([[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]])除读取外,我们还可以通过指定索引来将元素写入矩阵。
# 将第一行的第二列的数据改为9
x[1,2]=9
print(x)j结果如下:
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 9., 7.],
[ 8., 9., 10., 11.]])也可以按区域赋值
# 取0-1行的所有列更改为12
x[0:2,:]=12
print(x)结果如下:将第一个行和第二行的行列全部赋值成12了
tensor([[12., 12., 12., 12.],
[12., 12., 12., 12.],
[ 8., 9., 10., 11.]])有时候运行一些操作可能会导致新的变量分配内存,如
# id(y)则是这个y的标识
before=id(y)
y=y+x
id(y)==before由于中间操作了一步将x+y赋值给了y ,导致新开辟了空间,所以就等于false
结果:False
可以使用torch.zeros_like,这样更改了也会原地动作
z=torch.zeros_like(y)
print("id(z):",id(z))
print("z-before:",z)
z[:]=x+y
print("z-after:",z)
print("id(z):",id(z))结果如下:
id(z): 139337924747696
z-before: tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
z-after: tensor([[26., 25., 28., 27.],
[25., 26., 27., 28.],
[20., 21., 22., 23.]])
id(z): 139337924747696也可以这样使用y[:]=y+x或x+=y来保证原地操作:
before=id(y)
y[:]=y+x
id(y)==before结果:true
除了上面的功能,还可以很容易的转换,如转换numpy张量
import numpy
e=x.numpy()
f=torch.tensor(e)
print("numpy:",e)
print(f)
print(type(e))
print(type(f))结果如下:
numpy: [[12. 12. 12. 12.]
[12. 12. 12. 12.]
[ 8. 9. 10. 11.]]
tensor([[12., 12., 12., 12.],
[12., 12., 12., 12.],
[ 8., 9., 10., 11.]])
<class 'numpy.ndarray'>
<class 'torch.Tensor'>#将大小为1的张量转换为python标量
a=torch.tensor([3.5])
print(a)
print(a.item)
print(float(a))
print(int(a))结果:
tensor([3.5000])
<built-in method item of Tensor object at 0x7eba23772b10>
3.5本章节学习李沐老师的《深度学习课》