大家好,时间序列分析广泛用于预测和预报时间序列中的未来数据点,ARIMA模型被广泛用于时间序列预测,并被认为是最流行的方法之一。本文将介绍如何在Python中搭建和评估用于时间序列预测的ARIMA模型。
什么是ARIMA模型
ARIMA模型是一种用于分析和预测时间序列数据的统计模型。ARIMA方法明确适用于时间序列中的常见结构,为进行精确的时间序列预测提供了简单而强大的方法。
ARIMA是AutoRegressive Integrated Moving Average的缩写。它结合了三个关键方面:
-
自回归(AR):使用当前观测值与滞后观测值之间的相关性建立的模型。滞后观测值的数量称为滞后阶数或p。
-
积分(I):通过对原始观测值进行差分来使时间序列平稳。差分操作的次数称为d。
-
移动平均(MA):模型考虑了当前观测值与应用于过去观测值的移动平均模型的残差错误之间的关系。移动平均窗口的大小为阶数或q。
ARIMA模型的表示为ARIMA(p,d,q),其中p、d和q用整数值替代以指定所使用的确切模型。
采用ARIMA模型时的关键假设:
-
时间序列是由基础的ARIMA过程生成的。
-
参数p、d和q必须根据原始观测值进行适当的指定。
-
在拟合ARIMA模型之前,时间序列数据必须通过差分使其平稳。
-
如果模型拟合良好,残差应该是不相关且服从正态分布的。
总而言之,ARIMA模型为建模时间序列数据提供了结构化和可配置的方法,用于预测等目的,接下来将介绍如何在Python中拟合ARIMA模型。
Python代码示例
在本文中,我们将使用Kaggle上提供的Netflix证券数据来使用ARIMA模型预测Netflix证券价格。
- 数据加载
本示例将加载带有“日期”列作为索引的证券价格数据集。
import pandas as pd
net_df = pd.read_csv("Netflix_stock_history.csv", index_col="Date", parse_dates=True)
net_df.head(3)

- 数据可视化
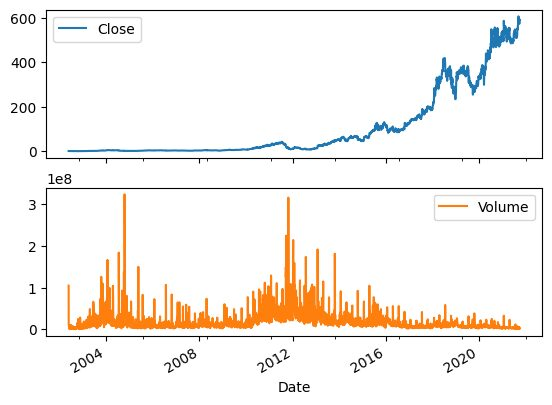
可以使用pandas的plot函数来可视化证券价格和成交量随时间的变化,很明显证券价格呈指数增长。
net_df[["Close","Volume"]].plot(subplots=True, layout=(2,1));
- 滚动预测ARIMA模型
本示例的数据集已经被分成训练集和测试集,并且开始训练ARIMA模型,然后进行了第一次预测。
使用通用的ARIMA模型得到了一个糟糕的结果,生成了一条平直的线。因此,本示例决定尝试滚动预测方法。
注意:代码示例是BOGDAN IVANYUK的notebook的修改版本。
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
train_data, test_data = net_df[0:int(len(net_df)*0.9)], net_df[int(len(net_df)*0.9):]
train_arima = train_data['Open']
test_arima = test_data['Open']
history = [x for x in train_arima]
y = test_arima
# 进行第一次预测
predictions = list()
model = ARIMA(history, order=(1,1,0))
model_fit = model.fit()
yhat = model_fit.forecast()[0]
predictions.append(yhat)
history.append(y[0])
在处理时间序列数据时,由于依赖于先前的观察结果,通常需要进行滚动预测,一种方法是在收到每个新观察结果后重新创建模型。
为了跟踪所有观察结果,可以手动维护一个名为history的列表,该列表最初包含训练数据,并在每次迭代时将新的观察结果追加到其中,这种方法可以帮助我们获得准确的预测模型。
# 滚动预测
for i in range(1, len(y)):
# 预测
model = ARIMA(history, order=(1,1,0))
model_fit = model.fit()
yhat = model_fit.forecast()[0]
# 反转转换预测值
predictions.append(yhat)
# 观察结果
obs = y[i]
history.append(obs)
- 模型评估
本示例的滚动预测ARIMA模型在简单实现的基础上显示出了100%的改进,产生了令人印象深刻的结果。
# 报告性能
mse = mean_squared_error(y, predictions)
print('MSE: '+str(mse))
mae = mean_absolute_error(y, predictions)
print('MAE: '+str(mae))
rmse = math.sqrt(mean_squared_error(y, predictions))
print('RMSE: '+str(rmse))
MSE: 116.89611817706545
MAE: 7.690948135967959
RMSE: 10.811850821069696
接下来将实际结果与预测结果进行可视化和比较,很明显,本示例的模型进行了高度准确的预测。
import matplotlib.pyplot as plt
plt.figure(figsize=(16,8))
plt.plot(net_df.index[-600:], net_df['Open'].tail(600), color='green', label = 'Train Stock Price')
plt.plot(test_data.index, y, color = 'red', label = 'Real Stock Price')
plt.plot(test_data.index, predictions, color = 'blue', label = 'Predicted Stock Price')
plt.title('Netflix Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Netflix Stock Price')
plt.legend()
plt.grid(True)
plt.savefig('arima_model.pdf')
plt.show()
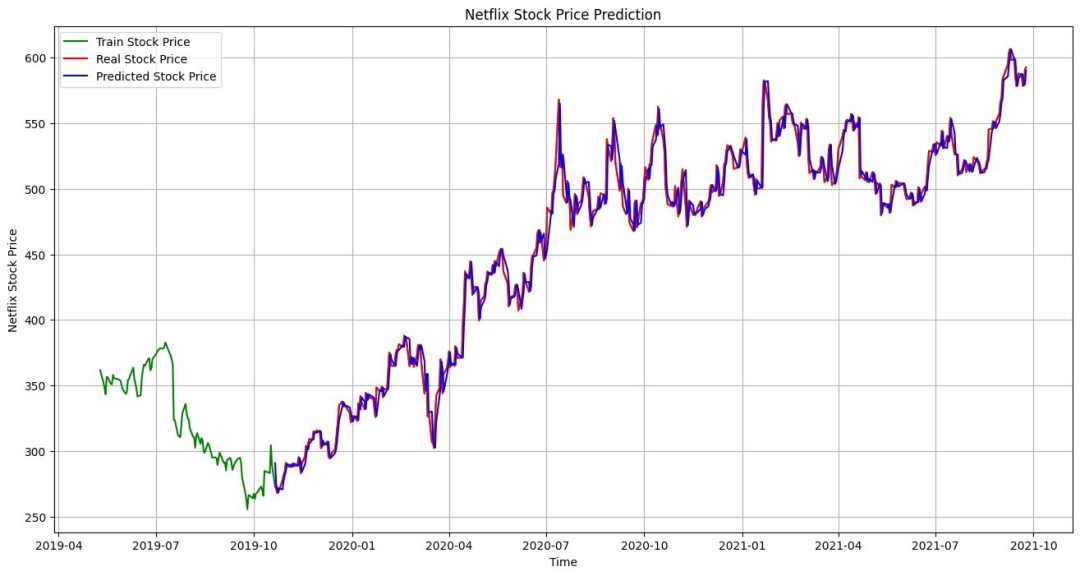
综上,在本文中我们提供了ARIMA模型的概述以及如何在Python中实现时间序列预测。ARIMA方法提供了一种灵活而结构化的方式进行时间序列数据建模,它依赖于先前的观察结果和过去的预测误差。