目录
一,关于A伴随,A逆与初等矩阵
二,分块矩阵
三,矩阵方程
一,关于A伴随,A逆与初等矩阵





 如何证明行列式的值不能是0;
如何证明行列式的值不能是0;








此秩为1.







 法一:
法一:
 法二:
法二:


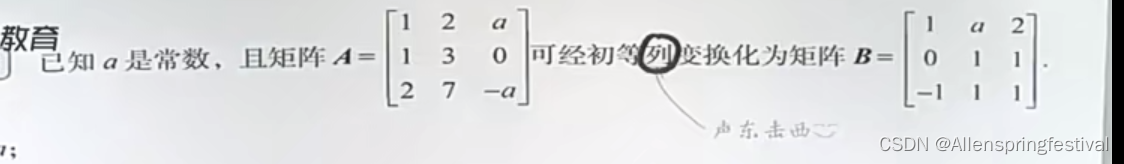 不用看是列变换还是行变换,我们需要从秩不变的性质去解题
不用看是列变换还是行变换,我们需要从秩不变的性质去解题








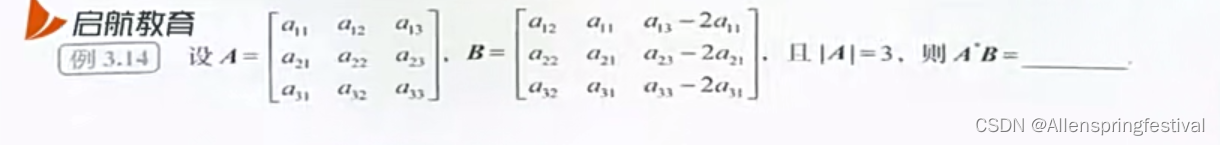



二,分块矩阵



左乘同行右乘同列,再加负号
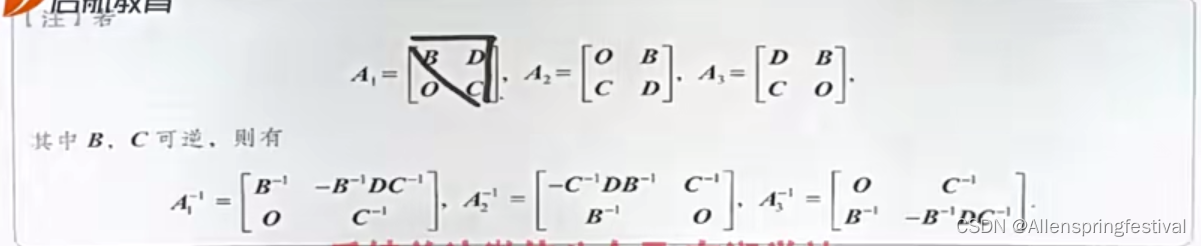
在副对角线上的需要先换位置(左撇右撇都要换),再左乘同行右乘同列,加上符号






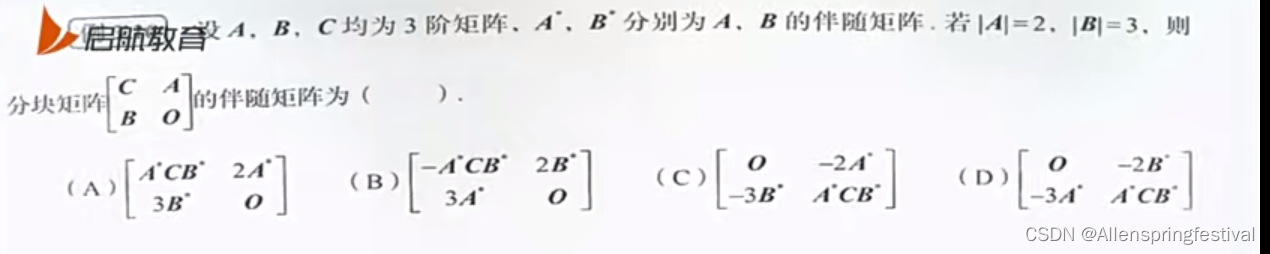


三,矩阵方程 



 A,B均不可相似对角化
A,B均不可相似对角化

在单位阵的基础上随便一个位置加上一个1,就不可以相似对角化。
最朴素的方法待定系数法:


因为P可逆,所以也需要加上条件


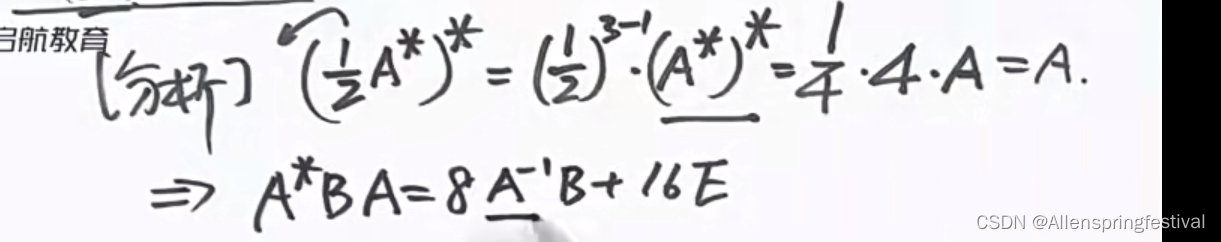




所以 a=2;



注意右边矩阵为自由项
设定克色i的值为为1,可以由左边矩阵求出次该向量
下面是特解

自由项都写0