【题目来源】
http://oj.ecustacm.cn/problem.php?id=1850
http://oj.ecustacm.cn/viewnews.php?id=1023
【题目描述】
给定 n 个小球,编号为 1-n,给定 m 个篮子,编号为 1-m。
每个球只允许放入样例给定的编号为 Ai 或者 Bi 的两个篮子中的 1 个。
每个球必须放入某个篮子。
如果篮子中球的数量为奇数,则该篮子是特殊的。
计算特殊的篮子最少有多少个。
【输入格式】
第一行为两个正整数 n 和 m,1≤n,m≤200000。表示 n 个小球,m 个篮子。
接下来 n 行,每行两个数字 Ai,Bi,表示第 i 个球可以放入 Ai 或者 Bi 编号的篮子。
1≤Ai,Bi≤m,Ai≠Bi。
【输出格式】
输出一个数字表示答案。
【输入样例】
4 3
1 2
2 3
1 3
1 2
【输入样例】
0
【算法分析】
◆ 异质图
本题本质上是异质图问题。异质图是一种具有多种节点类型或多种边类型的图数据结构,用于刻画复杂异质对象及其交互,具有丰富的语义信息。
本题异质图构建的依据是:将某球放入某个篮子,则此球与篮子之间就有连线,否则就没有连线。
依据本题样例,将第 i 个球放入 Ai 或者 Bi 编号的篮子中,可得出如下的异质图。其中,从某个小球引出的两条线,分别以一实线和一虚线表示(切记:根据题意,从某个小球引出的一实线和一虚线不能共存,只能取其一。此处都画出,只是为了示意)。
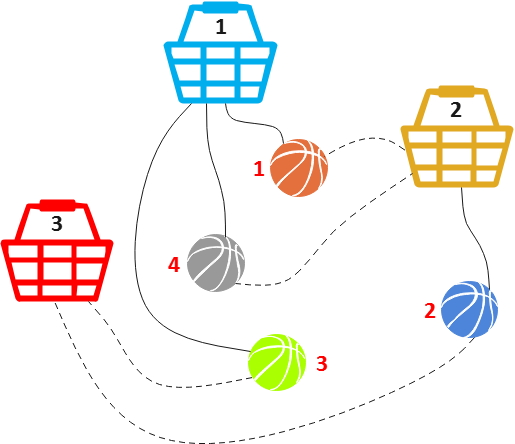
根据“从某个小球引出的一实线和一虚线不能共存,只能取其一”的约束,可得出符合本题题意的一种异质图。如下所示。
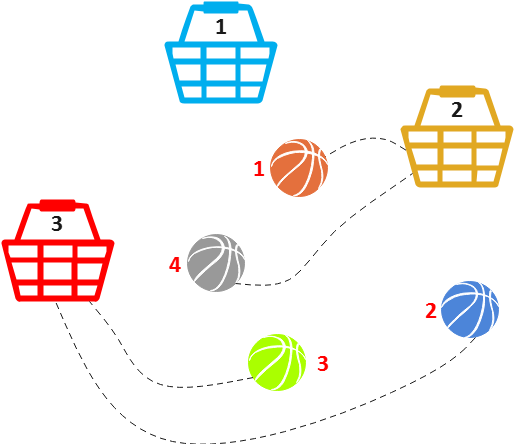
可见,若依据图论的观点,上面的示意图由若干个连通子图构成。那么问题来了。一个连通子图中,最少有多少个是特殊篮子?显然,如果连通子图中的线条是偶数,则特殊篮子最少为0个;如果连通子图中的线条是奇数,则特殊篮子最少为1个。
为了求解连通子图中的特殊篮子数,首选并查集。因为,并查集是求解判定连通子图相关问题的得力工具。
◆ 并查集
并查集模板:https://blog.csdn.net/hnjzsyjyj/article/details/120147618
int find(int x) {
if(x!=pre[x]) pre[x]=find(pre[x]);
return pre[x];
}
void merge(int x,int y) {
int p=find(x);
int q=find(y);
if(p!=q) pre[p]=q;
}并查集模板题之求团伙数量:https://blog.csdn.net/hnjzsyjyj/article/details/120120591
#include <bits/stdc++.h>
using namespace std;
const int maxn=100;
int pre[maxn];
int find(int x) { //寻找x的父节点
if(x!=pre[x]) pre[x]=find(pre[x]);
return pre[x];
}
void merge(int x,int y) { //合并两个子集
int p=find(x);
int q=find(y);
if(p!=q) pre[p]=q;
}
int main() {
int u,v,p,q;
int ans;
cin>>u>>v; //顶点数、边数
for(int i=1; i<=u; i++) //初始时每个节点的父节点都是自己
pre[i]=i;
for(int i=1; i<=v; i++) {
cin>>p>>q; //边的两个顶点序号
merge(p,q);
}
for(int i=1; i<=u; i++) {
if(find(i)==i) ans++; //计算连通子图个数,也就是得出几个团伙
}
cout<<ans<<endl;
return 0;
}
/*
in:
10 9
1 2
3 4
5 2
4 6
2 6
8 7
9 7
1 6
2 4
out:
3
*/
【算法代码】
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int cnt[maxn],pre[maxn],st[maxn];
int n,m;
int find(int x) {
if(x!=pre[x]) pre[x]=find(pre[x]);
return pre[x];
}
void merge(int x,int y) {
int p=find(x);
int q=find(y);
if(p!=q) {
pre[p]=q;
cnt[q]+=cnt[p]+1;
} else cnt[p]++;
}
int main() {
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++) pre[i]=i;
for(int i=1;i<=n;i++) {
int x,y;
scanf("%d %d",&x,&y);
merge(x,y);
}
int ans=0;
for(int i=1;i<=m;i++) {
int x=find(i);
if(!st[x]) {
if(cnt[x] & 1) ans++;
st[x]=1;
}
}
printf("%d",ans);
return 0;
}
/*
in:
4 3
1 2
2 3
1 3
1 2
out:
0
*/
【参考文献】
https://blog.csdn.net/weixin_43914593/article/details/131800622
https://blog.csdn.net/hnjzsyjyj/article/details/120120591
https://blog.csdn.net/hnjzsyjyj/article/details/120147618