在每个领域，都有国王，皇后，小兵和其他玩家。它们决定了该行业赖以生存的质量和标准。在同一领域，必然有赢家和输家。对于加密货币和代币经济来说，情况也是如此。本文的重点是代币经济的博弈论。它涉及游戏本身、谁在玩游戏、游戏规则和游戏模型。让我们了解一下博弈论的含义！

【什么是博弈论？】

“博弈论”这个词并不新鲜。博弈论研究的是经济主体的交互选择如何根据这些主体的偏好(或效用)产生相关的结果，而其中讨论的结果可能不是任何一个主体所期望的。

一般认为，游戏中的所有玩家都是理性的。这意味着无论你作为玩家有什么想法，其他玩家都可能有类似的想法。然而，区别在于个人在赢家和输家的游戏中领先的能力(Mooners和Exit Liquidity)。因此，要想成为游戏之王，就必须要有策略。

【策略】

策略是一种预先确定的“游戏计划”，它告诉玩家应该采取什么行动来应对其他玩家可能使用的每一种策略。策略分为以下几种：

• 纯粹策略：当策略在游戏中的每个决策点都指定了一个相同的特定行动时，就会出现这种情况。你正在监视鲸鱼玩家的钱包，你注意到他的策略非常纯粹，你可以预测他在任何时候的行动。
• 优势和劣势策略：这是玩家为确定最佳结果而采取的最优策略，且无论对手采取何种策略，都会将结果最大化。

当一个玩家的结果优于其他玩家的策略时，这个策略就是优势策略。假设有A和B玩家，如果A的策略优于B的策略，则A为劣势策略，B为劣势策略。当所有玩家都有一个优势策略时，优势策略会趋于均衡。也就是说，他们的决定和结果是一样的。这会使市场向同一方向移动，从而影响市场。

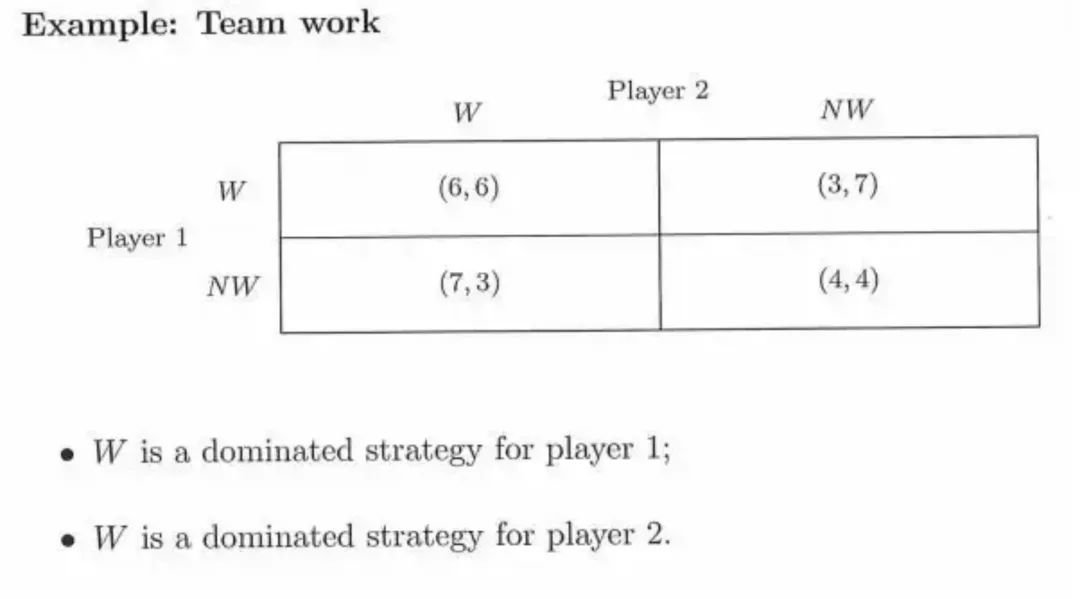▵ 玩家1{6>3 & 7>4}。玩家2{6>3 & 7>4}

• 最大化、极大化极小和极小化极大策略：这些策略深入研究了玩家在游戏行动中的个人偏好。也就是说，在市场中，玩家在资本差异和风险滞后的情况下进行博弈。随着优势策略和劣势策略的应用，最大化和极小化极大策略对在评估每个玩家和决定结果方面更加重要。

当玩家试图获取最大可能的利益时，就会出现最大化策略。这些玩家会冒着一切风险去寻求替代方案，其中包括即使可能会出现非常不利的结果，也要获得最佳结果的机会。

当玩家在最坏收益中选择最佳收益时，策略就是极大化极小的。在这种情况下，在市场交易中，有些人会冒着数千美元的风险，在交易中只赚取该金额的10%。这是极小化极大策略的一个很好的例子。

极小化极大策略是指玩家将对手或其他玩家的最佳收益最小化。这与极大化极小策略相反。它使用最小值来赚取最大值。如果有两个玩家，玩家2的极大化极小策略是玩家2在玩家1的策略下所能获得的最大收益。用一个简单的术语来说，这是在Degen游戏中很常见的退出流动性。

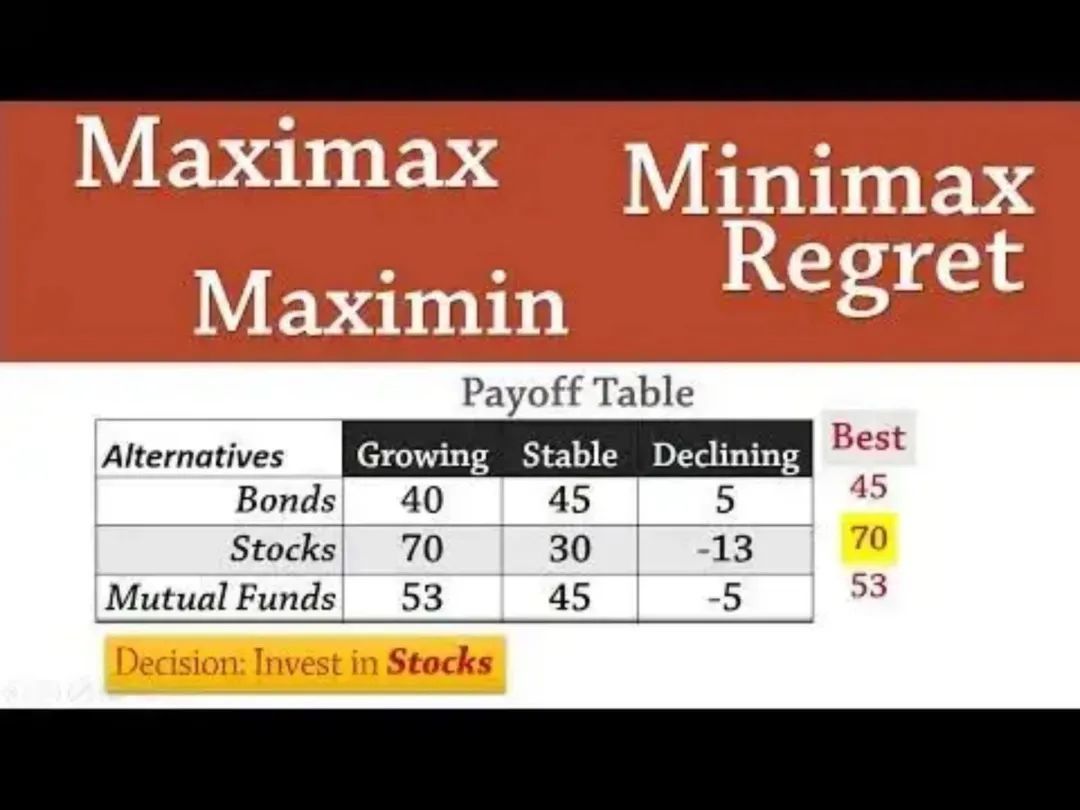▵最大化策略意味着他的交易都是最佳的。极大化极小策略是指他用最大值70美元来交易股票，以赚取最小的收益。极小化极大策略意味着他交易价值为5美元的债券。

注：收益是玩家在达到某种状态后所获得的结果。它可以是任何可量化的值。

【过渡到Web3】

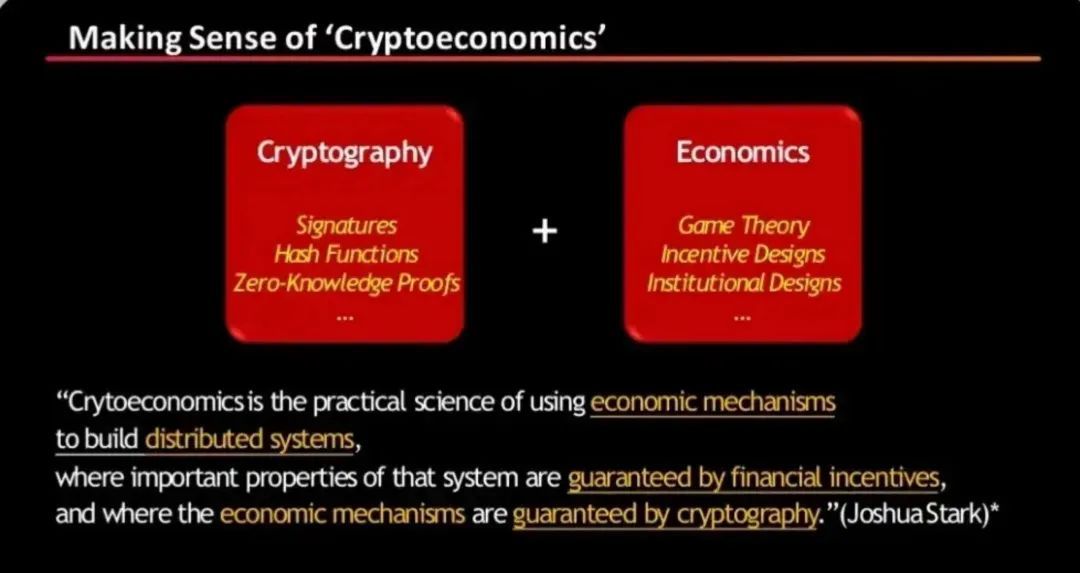
加密经济学结合了博弈论、经济学和密码学，以理解底层分布式区块链协议的激励模型。从博弈论的角度来理解理性节点在网络中的相互作用，可以增强分布式点对点系统的安全性和可持续性。需要注意的是，共识机制和工作证明等算法依赖于博弈论，以维持无信任的合作。他们帮助创造了一个：

1. 激励玩家获得预期结果
2. 设计一个基于代码而非人工中介的信任系统的游戏

加密货币博弈论的目标是模拟人类推理，以建立不需要任何疏忽，但对更大的利益有积极结果的网络。

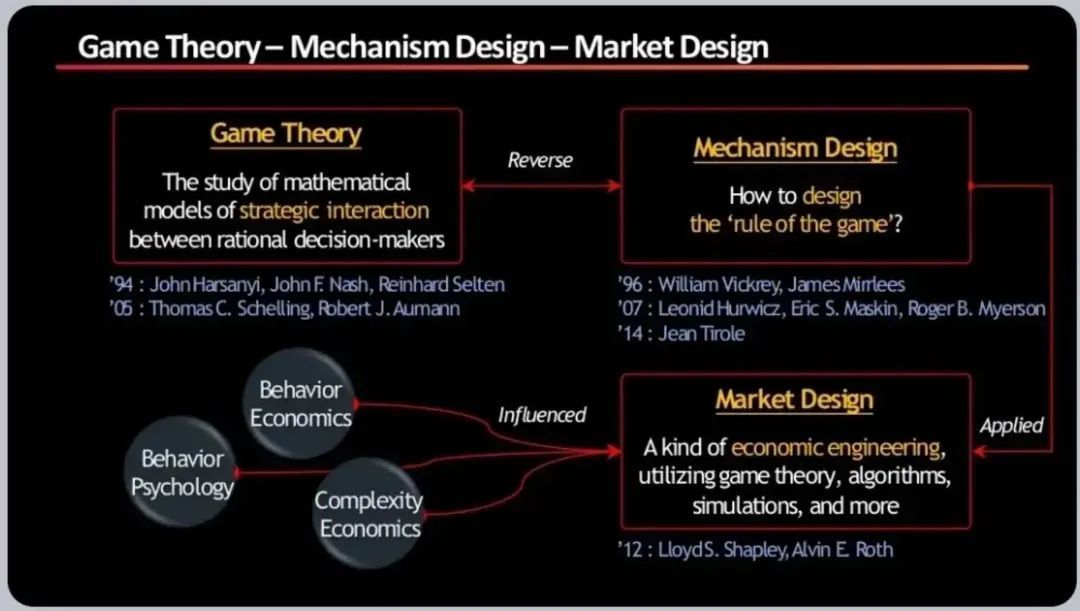
博弈论、行为经济学和市场设计让我们能够观察规则，以及人们如何在经济设计框架中与规则互动、规避规则和改变规则。在代币设计中被用来预测代币持有者对嵌入式激励的反应。

重要的是要注意，博弈论是经济设计框架中机制设计的反面。这是因为博弈论研究的是理性决策者之间战略互动的数学模式，而机制设计回答的是如何设计游戏规则本身的问题。

以下是游戏中需要考虑的问题。这适用于Web2和Web3环境中的主要情况。

• 玩家是否拥有充分或平等的信息？
• 玩家的利益是完全冲突的，还是有一些共同点？
• 合作协议是否具有可执行性？
• 游戏中的动作是连续的还是同时的？
• 游戏是只进行一次还是反复进行，对手是相同的还是不断变化的？

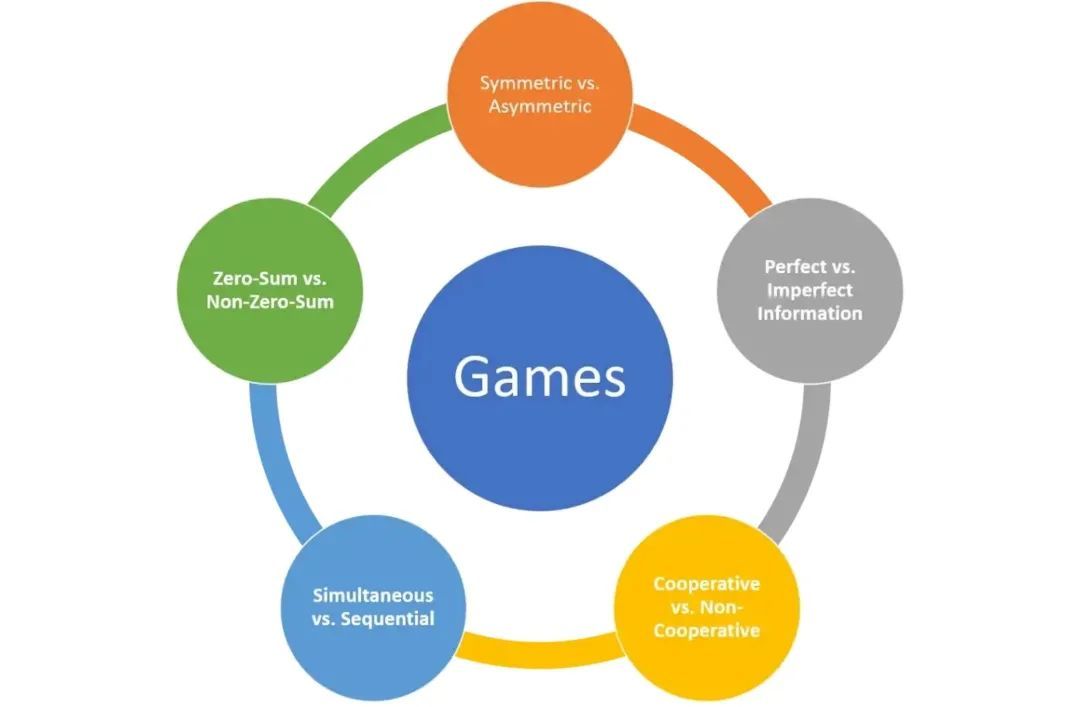当你开始研究Web 3中的协议时，这些都是你间接问自己的主要问题。

【博弈论模型】

博弈论模型是由一组玩家、一组可供每个玩家选择的行动(策略)以及对应于每种策略组合的收益向量表示的数学博弈。玩家既是买家也是卖家。每个玩家的动作是一组函数或保留价格(储备)。每个函数都将玩家的价值(对于买方)或成本(对于卖方)映射到价格。每个玩家的收益是该玩家在策略组合下的预期效用(或利润)。

博弈论模型的分类：

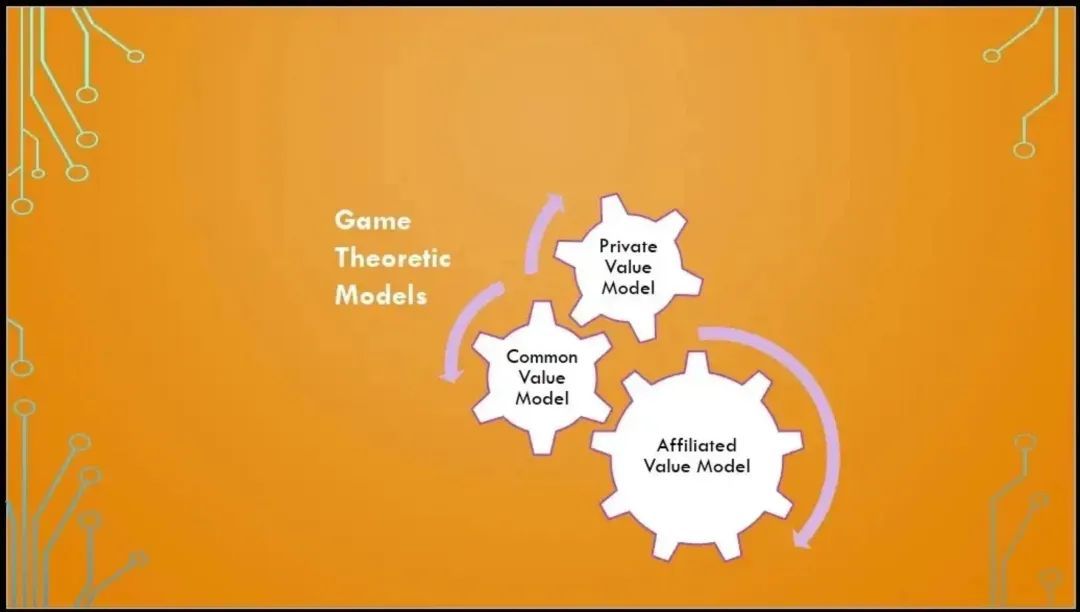
1. 私人价值模型：在这种情况下，每个玩家都假设每个竞争者会从分布(概率)中获得一个随机的私人价值。也就是说，项目的价值因人而异。
2. 公共价值模型：玩家对项目的代币有相同的估值，但他们没有关于这个估值的准确信息。在不知道准确估值的情况下，每个玩家都可以获得一个随机信号，用来从所有玩家共同的概率分布中消除真实的估值。这意味着，为了得出项目代币的确切价值，每个玩家都要进行研究，并获得对该项目真实价值的不同看法。私人模型的假设是，价值在各个玩家之间是独立的。然而，公共价值模型假设价值独立于概率分布的公共参数。
3. 关联价值模型：该模型结合了私人价值模型和公共价值模型的效用。用对称分析确定关于玩家的假设。

【代币设计中博弈论的实践说明】

代币建立在智能合约上。它们包含了代币分配、交换流程和入口维护的逻辑，被设计成具有激励机制，以确保参与者、用户或持有人因努力实现高质量的探索目标和充分阻止不当行为而得到奖励。

对于两名玩家，通常有两种可能的场景：

1. 候选人的质量有一个单一的阈值条件，要么是在超过阈值时买入，或者在质量低于阈值时卖出。我们所说的阈值指的是进场点
2. 当质量上有两个阈值时，结果要么总是低于一个阈值卖出，要么总是超过第二个阈值买入，介于这两个阈值之间的情况下，买入和卖出都会是稳定的结果。

对于两名以上的玩家，我们表明存在一个阈值，超过这个阈值就没有挑战，因此，结果总是买入，而低于这个阈值就会出现挑战。然而，有两种可能的平衡：

人人都买或人人都卖，这样就存在一个均衡问题。

这一分析并不排除可能存在买入的阈值满足某种“严格改善”的效用，买入的代币项目价值严格优于没有买入的项目的价值的情况。如果该效用仍然有效，那么对于项目及其参与者来说，就会有一个有趣的反直觉的暗示。

对于博弈以“均衡选择”问题结束的情况，我们进一步考虑了被称为“收益主导均衡”的针对纳什均衡概念的改进，这是一个帕累托最优的纳什均衡。对于2人博弈和n人博弈，我们在候选质量上确定了一个共同的附加阈值条件，将“所有玩家都买入”和“所有玩家都卖出”分开，作为与收益主导均衡相对应的结果。

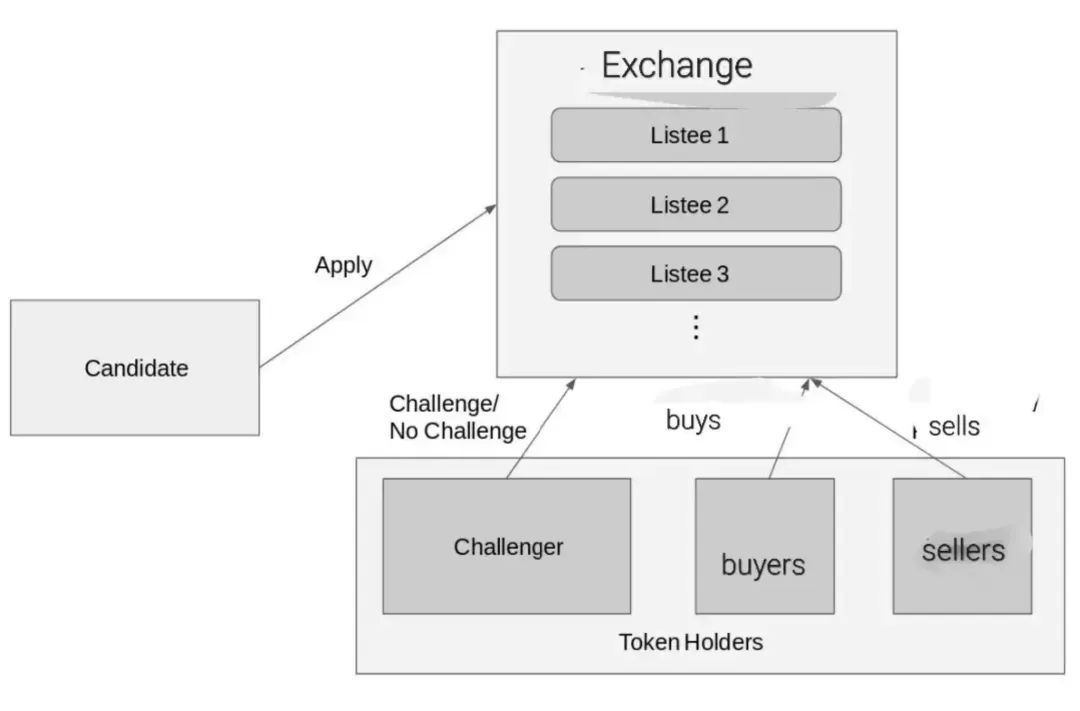基本模型

根据理论知识，我们将注意力集中在这样一种情况：有一个新的候选人愿意将一些代币存入交易所。挑战者(可能是鲸鱼)可能有兴趣利用这样的候选人作为退出的流动性，当他与其他玩家进入资金池时，会与他玩一场心理游戏。

如果挑战成功，挑战者和其他被确定的玩家将在盈利的同时获得一些代币，而那些与候选人走同一条路的玩家将遭受损失。

如果没有挑战，所有人都会全力以赴，他们要么都持有，要么都卖出，这取决于各自玩家的研究类型或感知价值。我们假设代币的价值会单向增加项目的质量，因此，玩家有动机增加或减少项目的声誉。

考虑到：

D->存款。

d->挑战后获得或失去的金额。

Q->对挑战者的行动或决定买账的百分比。

S->损益之比。

游戏、收益和激励机制：

• 集中总代币(T/P)。
• 挑战者持有的代币。(Tc)
• 跟随挑战者行动的代币(Ta)。
• 其他行动的代币(Tr = T-Ta)。也就是总代币数减去跟随挑战者行动的代币数。
• 在假设他们拒绝了挑战者的行动的前提下，响应挑战者的行动而购买候选人行动的比率：(Wa = Ta / T)。

其他的概念有：

候选人的真实价值/价值比(r)和初始代币估值(V0)。

随着游戏的开始：

• 如果候选人接受了挑战者的行为，那么在正确的行动下，他就成功地买入了盈利的代币。因此{Wa > Q}
• 如果候选人拒绝挑战者的行动，他就会被用作退出的流动性。因此{Wa < Q}

在第一个场景中，候选人获得(D*d)代币。在此过程中拒绝挑战者行动的人获得{D*(1-d) + (Tr-Tc)}*s。这意味着，挑战者将他的存款输给了候选人和那些跟随他行动的人。然而，那些跟随挑战者行动的人失去了他们代币中的’s’部分。

在第二种情况下，挑战者获得(D*d)代币作为利润。跟随他行动的人得到{D*(1-d) +Ta}*s。候选人成功地被利用为EL，他失去了他的存款。那些遵循这个决定的人失去了他们代币中的’s’部分。

这就是游戏的基本方法。挑战者和候选人的行为会受到许多因素的影响。研究个人价值和观点以及所使用的策略是必要且重要的。激励、均衡、结果分析、收益主导均衡和其他重要分析都是为了确定谁在什么方面取得成功，以及如何取得成功。

文章转载自RubiksWeb3

原文来自：https://crypoe.com/article/7797