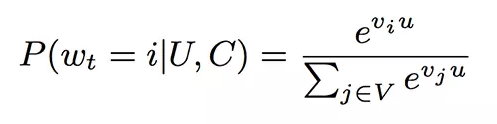文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 进阶
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 证明
- 代码
- 复杂度分析
题目
标题和出处
标题:相交链表
出处:160. 相交链表
难度
2 级
题目描述
要求
给你两个单链表的头结点 headA \texttt{headA} headA 和 headB \texttt{headB} headB,请你找出并返回两个单链表相交的起始结点。如果两个链表不存在相交结点,返回 null \texttt{null} null。
图示两个链表在结点 c1 \texttt{c1} c1 开始相交:

题目数据保证整个链式结构中不存在环。
注意,函数返回结果后,链表必须保持其原始结构。
自定义评测:
评测系统的输入如下(你设计的程序不适用此输入):
- intersectVal \texttt{intersectVal} intersectVal——相交的起始结点的值。如果不存在相交结点,这一值为 0 \texttt{0} 0。
- listA \texttt{listA} listA——第一个链表。
- listB \texttt{listB} listB——第二个链表。
- skipA \texttt{skipA} skipA——在 listA \texttt{listA} listA 中(从头结点开始)跳到交叉结点的结点数。
- skipB \texttt{skipB} skipB——在 listB \texttt{listB} listB 中(从头结点开始)跳到交叉结点的结点数。
评测系统将根据这些输入创建链式数据结构,并将两个头结点 headA \texttt{headA} headA 和 headB \texttt{headB} headB 传递给你的程序。如果程序能够正确返回相交结点,那么你的解决方案将被视作正确答案。
示例
示例 1:

输入:
intersectVal
=
8,
listA
=
[4,1,8,4,5],
listB
=
[5,6,1,8,4,5],
skipA
=
2,
skipB
=
3
\texttt{intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3}
intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:
Intersected
at
‘8’
\texttt{Intersected at `8'}
Intersected at ‘8’
解释:相交结点的值为
8
\texttt{8}
8(注意,如果两个链表相交则不能为
0
\texttt{0}
0)。
从各自的表头开始算起,链表
A
\texttt{A}
A 为
[4,1,8,4,5]
\texttt{[4,1,8,4,5]}
[4,1,8,4,5],链表
B
\texttt{B}
B 为
[5,6,1,8,4,5]
\texttt{[5,6,1,8,4,5]}
[5,6,1,8,4,5]。
在
A
\texttt{A}
A 中,相交结点前有
2
\texttt{2}
2 个结点;在
B
\texttt{B}
B 中,相交结点前有
3
\texttt{3}
3 个结点。
示例 2:

输入:
intersectVal
=
2,
listA
=
[1,9,1,2,4],
listB
=
[3,2,4],
skipA
=
3,
skipB
=
1
\texttt{intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1}
intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:
Intersected
at
‘2’
\texttt{Intersected at `2'}
Intersected at ‘2’
解释:相交结点的值为
2
\texttt{2}
2(注意,如果两个链表相交则不能为
0
\texttt{0}
0)。
从各自的表头开始算起,链表
A
\texttt{A}
A 为
[1,9,1,2,4]
\texttt{[1,9,1,2,4]}
[1,9,1,2,4],链表
B
\texttt{B}
B 为
[3,2,4]
\texttt{[3,2,4]}
[3,2,4]。
在
A
\texttt{A}
A 中,相交结点前有
3
\texttt{3}
3 个结点;在
B
\texttt{B}
B 中,相交结点前有
1
\texttt{1}
1 个结点。
示例 3:

输入:
intersectVal
=
0,
listA
=
[2,6,4],
listB
=
[1,5],
skipA
=
3,
skipB
=
2
\texttt{intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2}
intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:
No
intersection
\texttt{No intersection}
No intersection
解释:从各自的表头开始算起,链表
A
\texttt{A}
A 为
[2,6,4]
\texttt{[2,6,4]}
[2,6,4],链表
B
\texttt{B}
B 为
[1,5]
\texttt{[1,5]}
[1,5]。
由于这两个链表不相交,所以
intersectVal
\texttt{intersectVal}
intersectVal 必须为
0
\texttt{0}
0,而
skipA
\texttt{skipA}
skipA 和
skipB
\texttt{skipB}
skipB 可以是任意值。
这两个链表不相交,因此返回
null
\texttt{null}
null。
数据范围
- listA \texttt{listA} listA 中结点数目为 m \texttt{m} m
- listB \texttt{listB} listB 中结点数目为 n \texttt{n} n
- 1 ≤ m, n ≤ 3 × 10 4 \texttt{1} \le \texttt{m, n} \le \texttt{3} \times \texttt{10}^\texttt{4} 1≤m, n≤3×104
- 1 ≤ Node.val ≤ 10 5 \texttt{1} \le \texttt{Node.val} \le \texttt{10}^\texttt{5} 1≤Node.val≤105
- 0 ≤ skipA ≤ m \texttt{0} \le \texttt{skipA} \le \texttt{m} 0≤skipA≤m
- 0 ≤ skipB ≤ n \texttt{0} \le \texttt{skipB} \le \texttt{n} 0≤skipB≤n
- 如果 listA \texttt{listA} listA 和 listB \texttt{listB} listB 没有交点, intersectVal \texttt{intersectVal} intersectVal 为 0 \texttt{0} 0
- 如果 listA \texttt{listA} listA 和 listB \texttt{listB} listB 有交点, intersectVal = listA[skipA] = listB[skipB] \texttt{intersectVal} = \texttt{listA[skipA]} = \texttt{listB[skipB]} intersectVal=listA[skipA]=listB[skipB]
进阶
你能否设计一个时间复杂度 O(m + n) \texttt{O(m + n)} O(m + n)、空间复杂度 O(1) \texttt{O(1)} O(1) 的解法?
解法一
思路和算法
如果两个链表相交,则一定存在一个相交的起始结点,从链表相交的起始结点到链表末尾结点的全部结点是两个链表共用的结点。遍历两个链表各一次,则两个链表共用的结点会被重复访问,第一个被重复访问的结点即为链表相交的起始结点。
如果两个链表不相交,则不存在两个链表共用的结点。遍历两个链表各一次,任何结点都不会被重复访问。
因此可以遍历两个链表各一次,根据是否有结点被重复访问判断两个链表是否相交。为了判断是否有结点被重复访问,可以使用哈希集合存储访问过的结点。
首先遍历链表 listA \textit{listA} listA,将每个结点加入哈希集合,然后遍历链表 listB \textit{listB} listB,对于链表 listB \textit{listB} listB 中遍历到的每个结点判断是否在哈希集合中。在遍历链表 listB \textit{listB} listB 的过程中遇到的第一个在哈希集合中的结点即为链表相交的起始结点,返回该结点。如果遍历链表 listB \textit{listB} listB 结束之后仍没有遇到在哈希集合中的结点,则两个链表不相交,返回 null \text{null} null。
代码
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
Set<ListNode> visited = new HashSet<ListNode>();
ListNode temp = headA;
while (temp != null) {
visited.add(temp);
temp = temp.next;
}
temp = headB;
while (temp != null) {
if (visited.contains(temp)) {
return temp;
}
temp = temp.next;
}
return null;
}
}
复杂度分析
-
时间复杂度: O ( m + n ) O(m + n) O(m+n),其中 m m m 和 n n n 分别是链表 listA \textit{listA} listA 和 listB \textit{listB} listB 的结点数。需要遍历两个链表各一次。
-
空间复杂度: O ( m ) O(m) O(m),其中 m m m 是链表 listA \textit{listA} listA 的长度。需要使用哈希集合存储链表 listA \textit{listA} listA 中的全部结点。
解法二
思路和算法
解法一使用哈希表,空间复杂度是 O ( m ) O(m) O(m)。使用双指针可以将空间复杂度降低到 O ( 1 ) O(1) O(1)。
创建两个指针 pointer 1 \textit{pointer}_1 pointer1 和 pointer 2 \textit{pointer}_2 pointer2,指针 pointer 1 \textit{pointer}_1 pointer1 依次遍历链表 listA \textit{listA} listA 和链表 listB \textit{listB} listB 的每个结点,指针 pointer 2 \textit{pointer}_2 pointer2 依次遍历链表 listB \textit{listB} listB 和链表 listA \textit{listA} listA 的每个结点,初始时分别指向两个链表的头结点 headA \textit{headA} headA 和 headB \textit{headB} headB。
指针 pointer 1 \textit{pointer}_1 pointer1 的遍历过程是:从 headA \textit{headA} headA 开始依次遍历链表 listA \textit{listA} listA 的每个结点,当遍历完链表 listA \textit{listA} listA 之后, pointer 1 \textit{pointer}_1 pointer1 指向 null \text{null} null,下一步 pointer 1 \textit{pointer}_1 pointer1 指向 headB \textit{headB} headB,然后依次遍历链表 listB \textit{listB} listB 的每个结点,当遍历完链表 listB \textit{listB} listB 之后, pointer 1 \textit{pointer}_1 pointer1 指向 null \text{null} null。
指针 pointer 2 \textit{pointer}_2 pointer2 的遍历过程和指针 pointer 1 \textit{pointer}_1 pointer1 的遍历过程相似,区别在于指针 pointer 2 \textit{pointer}_2 pointer2 先遍历链表 listB \textit{listB} listB 后遍历链表 listA \textit{listA} listA。
两个指针的遍历同步进行,每次两个指针同时移动,直到两个指针指向同一个结点或者同时指向 null \text{null} null。
-
如果两个指针指向同一个结点,则该结点即为链表相交的起始结点,返回该结点。
-
如果两个指针同时指向 null \text{null} null,则两个链表不相交,返回 null \text{null} null。
证明
双指针解法的正确性证明需要考虑两种情况,第一种情况是两个链表相交,第二种情况是两个链表不相交。
如果两个链表相交,假设两个链表在相交之前的部分各有 x x x 个结点和 y y y 个结点,共用的部分有 z z z 个结点,则 x + z = m x + z = m x+z=m, y + z = n y + z = n y+z=n,其中 m m m 和 n n n 分别是链表 listA \textit{listA} listA 和 listB \textit{listB} listB 的结点数。
-
如果 x = y x = y x=y,则两个指针同时到达链表相交的起始结点。
-
如果 x ≠ y x \ne y x=y,则指针 pointer 1 \textit{pointer}_1 pointer1 从 headA \textit{headA} headA 开始移动 m + y + 1 m + y + 1 m+y+1 次之后到达链表相交的起始结点(从 null \text{null} null 移动到 headB \textit{headB} headB 也是一次移动),指针 pointer 2 \textit{pointer}_2 pointer2 从 headB \textit{headB} headB 开始移动 n + x + 1 n + x + 1 n+x+1 次之后到达链表相交的起始结点(从 null \text{null} null 移动到 headA \textit{headA} headA 也是一次移动),由于 m + y + 1 = n + x + 1 = x + y + z + 1 m + y + 1 = n + x + 1 = x + y + z + 1 m+y+1=n+x+1=x+y+z+1,因此两个指针同时到达链表相交的起始结点。
如果两个链表不相交,则两个指针一定会在移动相同次数之后同时指向 null \text{null} null。
-
如果 m = n m = n m=n,则两个链表的结点数相同,两个指针遍历两个链表同时结束,因此同时指向 null \text{null} null。
-
如果 m ≠ n m \ne n m=n,则指针 pointer 1 \textit{pointer}_1 pointer1 从 headA \textit{headA} headA 开始移动 m + n + 1 m + n + 1 m+n+1 次之后指向 null \text{null} null(从 null \text{null} null 移动到 headB \textit{headB} headB 也是一次移动),指针 pointer 2 \textit{pointer}_2 pointer2 从 headA \textit{headA} headA 开始移动 n + m + 1 n + m + 1 n+m+1 次之后指向 null \text{null} null(从 null \text{null} null 移动到 headA \textit{headA} headA 也是一次移动),由于 m + n + 1 = n + m + 1 m + n + 1 = n + m + 1 m+n+1=n+m+1,因此两个指针同时指向 null \text{null} null。
代码
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode pointer1 = headA, pointer2 = headB;
while (pointer1 != pointer2) {
pointer1 = pointer1 == null ? headB : pointer1.next;
pointer2 = pointer2 == null ? headA : pointer2.next;
}
return pointer1;
}
}
复杂度分析
-
时间复杂度: O ( m + n ) O(m + n) O(m+n),其中 m m m 和 n n n 分别是链表 listA \textit{listA} listA 和 listB \textit{listB} listB 的结点数。最坏情况下,每个指针遍历两个链表各一次。
-
空间复杂度: O ( 1 ) O(1) O(1)。







![[C/C++/初学者]500以内的亲密数对(VS2012)](https://img-blog.csdnimg.cn/f2a700d1545e432681b598878c437759.png)
![[附源码]Python计算机毕业设计高校体育馆管理信息系统Django(程序+LW)](https://img-blog.csdnimg.cn/feb0445aa59b442d84908465cdf1a666.png)