A. Unit Array

Problem - A - Codeforces

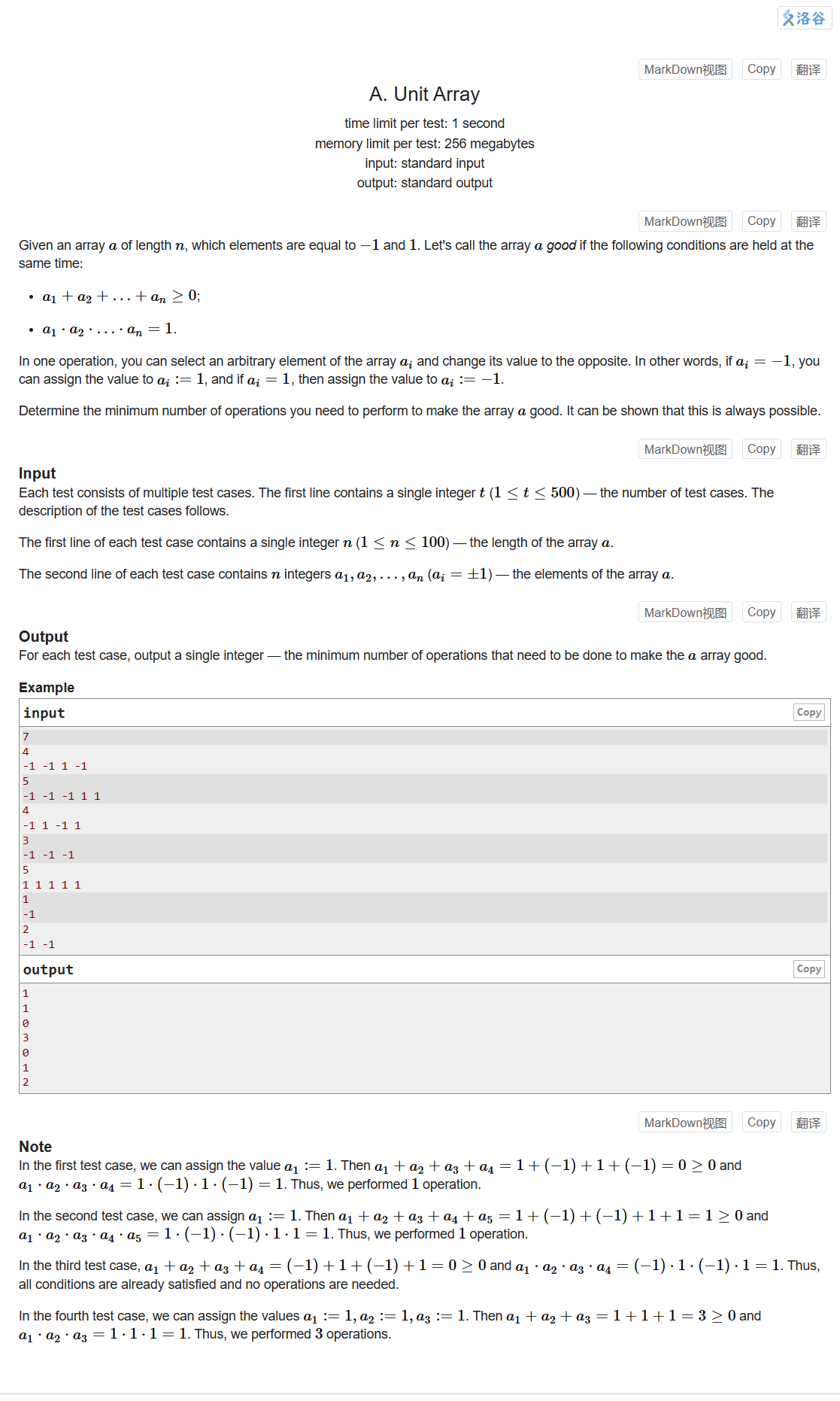
统计-1的数量cnt，当cnt为奇数或者n-cnt-cnt < 0（1的数量小于-1的数量）时，ans++，cnt–

#include <iostream>
using namespace std;

const int N = 110;
int T, a[N];

int main()
{
    cin >> T;
    while ( T -- )
    {
        int n, cnt = 0, ans = 0;
        cin >> n;
        for (int i = 0; i < n; ++ i ) 
        {
            cin >> a[i];
            if (a[i] == -1) cnt ++ ;
        }
        while (cnt & 1 || n - cnt - cnt < 0) cnt -- , ans ++ ;
        cout << ans << endl;
    }
    return 0;
}

---

B. Maximum Strength

Problem - B - Codeforces

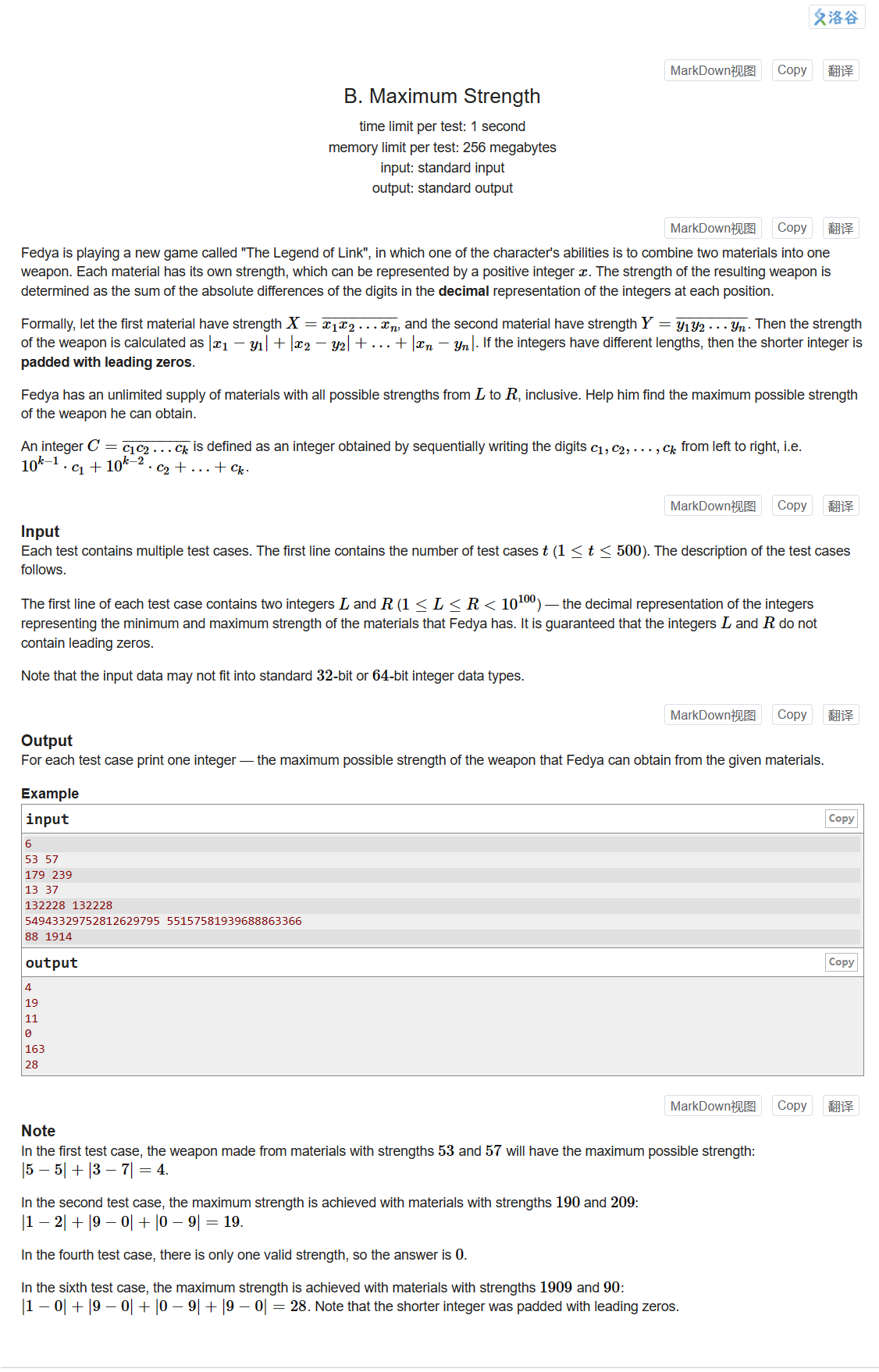
给定最大最小值范围，计算每个数位之差，使之最大
最小值的第i位，增大到0，最大值的第i位减小到0，此时数位差最大
什么情况下不能进行以上构造？两串长度相同（不同时用前导零填充），从左往右遍历时，若前缀相同，则不能进行构造，数位差为$|s[i]-t[i]|$。只要前缀不同，就能进行构造
比如：1234, 0244，一开始默认前缀相同，数位差为1，之后就能构造出3个9
即1000和0999
1234，1244，直到第4位时前缀才不同，数位差为：0+0+1，最后构造一个9
即1230和1249

#include <iostream>
#include <string>
using namespace std;

int T;
string down, up;

int main()
{
    cin >> T;
    while ( T -- )
    {
        cin >> down >> up;
        int di = 0, ui = 0, ans = 0;
        bool flag = true; // 前缀是否相等
        down = string(up.size() - down.size(), '0') + down;
        
        for (; di < down.size(); ++ di, ++ ui )
        {
            if (flag) 
            {
                ans += abs(up[ui] - down[di]);
                if (up[ui] != down[di]) flag = false;
            }
            else ans += 9;
        }
        cout << ans << endl;
    }
    return 0;
}

---

C. Game with Reversing

Problem - C - Codeforces

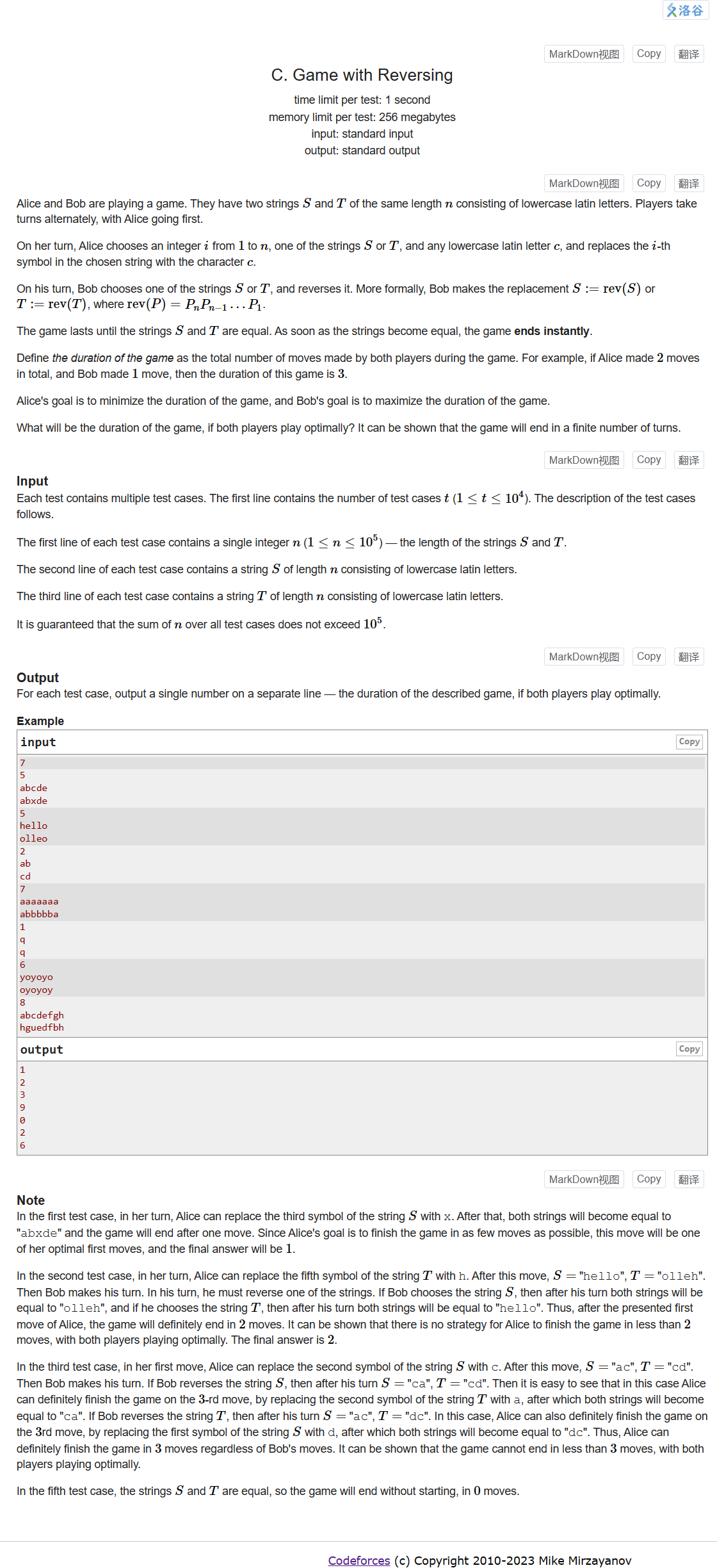
看起来是一道博弈论的题，有些不敢做，但是分析之后就会发现这和博弈论没啥关系
A每次修改t串中的一个字符，使之最终等于s串
B每次会反转t串或s串，不可以不反转

假设只有A进行操作，统计t和s不同字符个数cnt，cnt次之后两串相等。若B进行了操作，无论B反转s还是t，反转偶数次等价于没有反转
cnt = 1, ans = 1，A先修改
cnt = 2, ans = 4，A先修改，B反转，A再修改，此时两串反转后才相等，所以需要等B反转
cnt = 3, ans = 5
cnt = 4, ans = 8
发现规律，若cnt为偶数，ans为2 * cnt，cnt为奇数，ans为2 * cnt - 1
注意，cnt指的是没有反转t串时，t和s的不同字符
若反转t串后，两者的不同字符小于反转前，情况又不一样
样例：
hello
olleo
此时再找相应的规律即可

#include <iostream>
#include <string>
#include <algorithm>
using namespace std;

int T, n;
string s, t;

int main()
{
    cin >> T;
    while ( T -- )
    {
        int cnt1 = 0, cnt2 = 0;
        cin >> n >> s >> t;
        for (int i = 0; i < s.size(); ++ i ) if (s[i] != t[i]) cnt1 ++ ;
        reverse(t.begin(), t.end());
        for (int i = 0; i < s.size(); ++ i ) if (s[i] != t[i]) cnt2 ++ ;
        int cnt = min(cnt1, cnt2);
        if (cnt == 0) printf("%d\n", 0 + cnt1 ? 2 : 0);
        else if (cnt & 1) printf("%d\n",cnt * 2 - (cnt1 <= cnt2));
        else printf("%d\n", cnt * 2- (cnt2 <= cnt1));
    }
    return 0;
}

---

D. Survey in Class

Problem - D - Codeforces

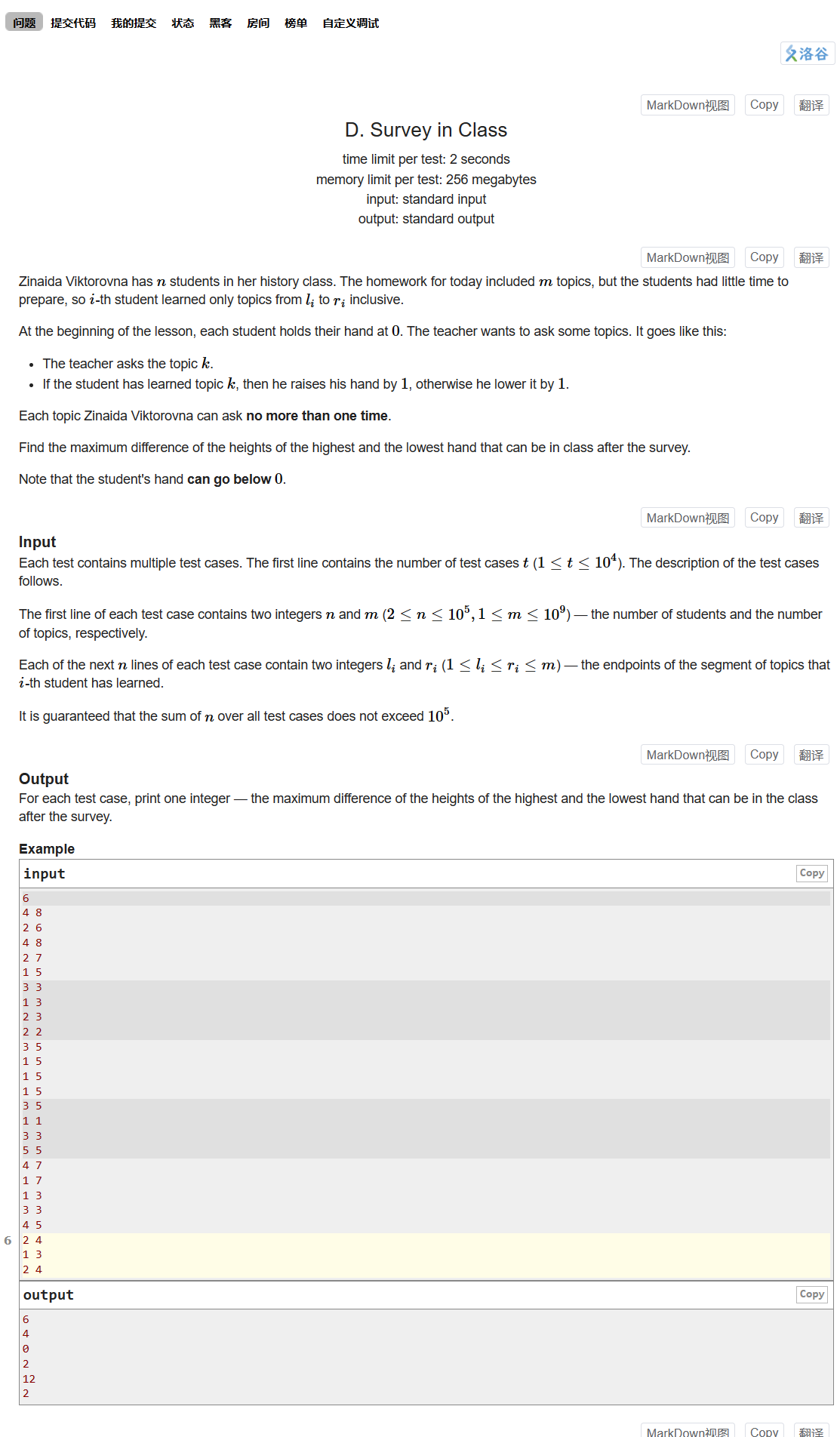
给定m个闭区间，区间中所有数的范围在1~n之间，从1~n之间选择一些数作为集合s。若集合s中的数出现在区间中，则区间得分+1，否则区间得分-1
问区间的得分最大与得分最小值的最大差值为多少？
考虑如何构造得分最高的区间，选择区间中的所有数作为集合s即可，此时考虑得分最小的区间是怎样的？让集合s中的数尽可能地不在该区间中，那么该区间的得分最低
构造最高得分区间时分情况讨论：

1. 右端点最小的区间
2. 左端点最大的区间
3. 在该区间中，区间长度最小的区间

如下图，在三种情况中取阴影部分最大的情况，遍历所有区间，将每个区间都构造成得分最高区间，取所有情况的最大值

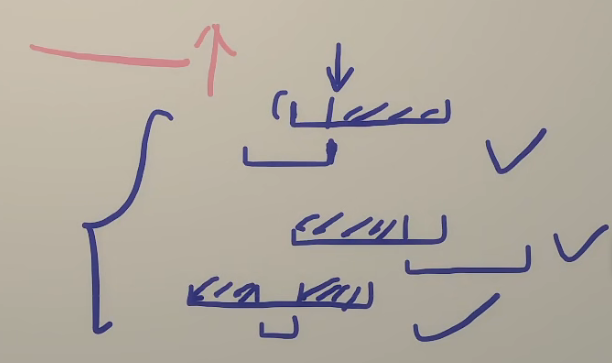
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 2e5 + 10;
int T, n, m;
int l[N], r[N];

int main()
{
    cin >> T;
    while ( T -- )
    {
        cin >> n >> m;
        int rmin = 0x3f3f3f3f, lmax = 0, lenmin = 0x3f3f3f3f;
        for (int i = 0; i < n; ++ i )
        {
            cin >> l[i] >> r[i];
            rmin = min(rmin, r[i]);
            lmax = max(lmax, l[i]);
            lenmin = min(lenmin, r[i] - l[i] + 1);
        }
        int ans = 0;
        for (int i = 0; i < n; ++ i )
            ans = max({ans, r[i] - max(l[i] -1, rmin), min(r[i] + 1, lmax) - l[i], r[i] - l[i] + 1 - lenmin});
        
        cout << 2 * ans << endl;
    }
    return 0;
}

---

E. MEX of LCM

Problem - E - Codeforces

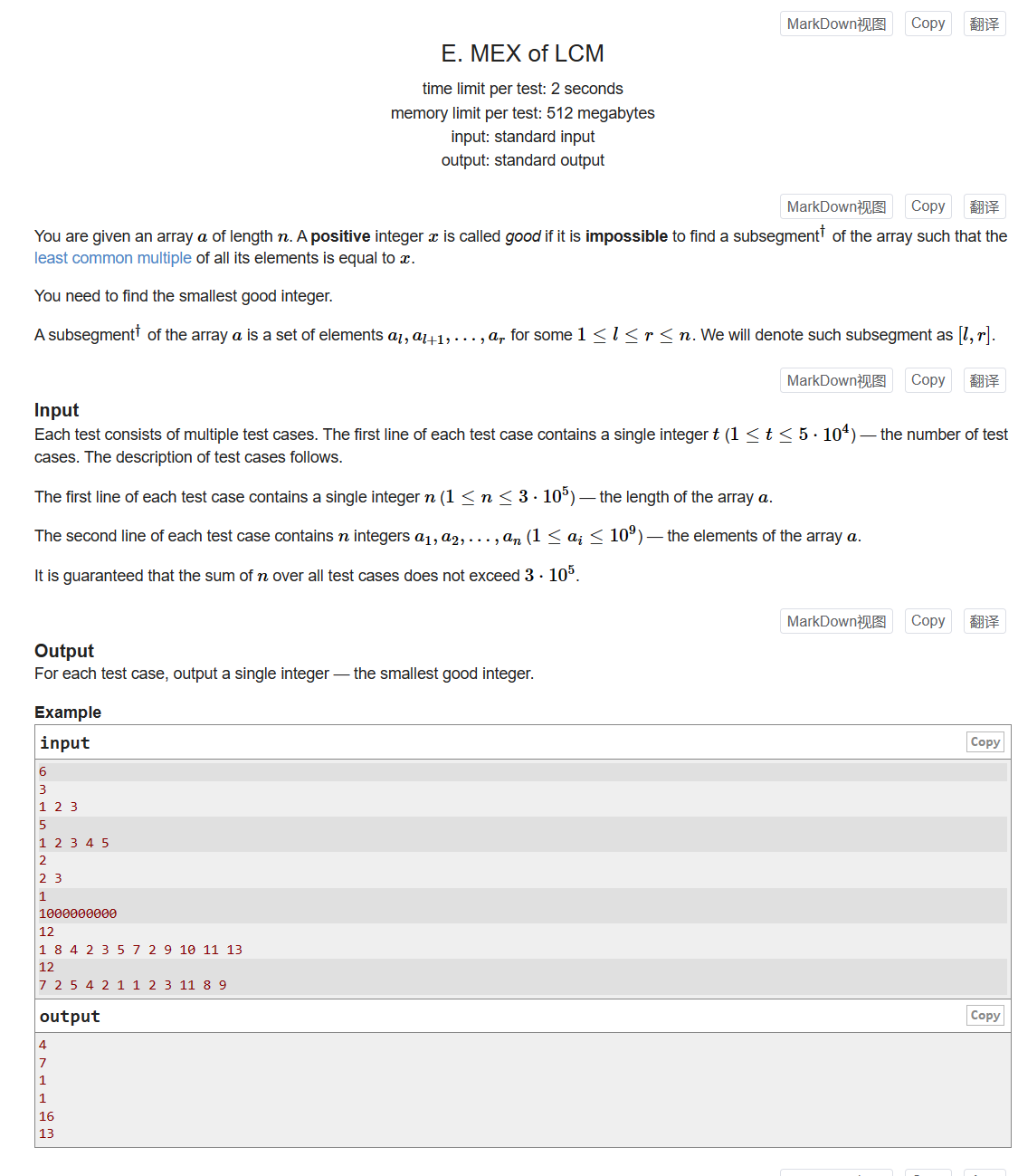
n个数的数组，会产生$n^2$个子数组，那么最多有$n^2$个lcm
暴力枚举每个子数组不可取，以集合的角度考虑，所有子数组可以划分成n个集合，第i个集合由以$a_i$结尾的子数组组成，这样的划分不重不漏
根据lcm的结合律，从1~n枚举每个集合，用$s_i$表示第i个集合中所有子数组的lcm集合。计算$s_{i+1}$时，$s_{i+1}$中除了$a_{i+1}$，其他数都是$a_{i+1}$与$s_i$进行lcm后的结果
从1~n计算所有集合，将每个集合$s_i$保存到集合ans中，暴力遍历ans找到不在ans中的最小正整数即可

小于n的素数数量为$O(n/log(n))$（增长速度）

#include <iostream>
#include <set>
using namespace std;

typedef long long LL;
const int N = 3e5 + 10, INF = 1e9;
int a[N], T, n;

LL gcd(LL a, LL b)
{
    return b ? gcd(b, a % b) : a;
}

LL lcm(LL a, LL b)
{
    return a * b / gcd(a, b);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> T;
    while ( T -- )
    {
        cin >> n;
        for (int i = 0; i < n; ++ i ) cin >> a[i];
        set<LL> ans, pre;
        for (int i = 0; i < n; ++ i )
        {
            set<LL> cur;
            for (auto t : pre)
            {
                int u = lcm(t, a[i]);
                if (u < INF)
                {
                    ans.insert(u);
                    cur.insert(u);
                }
            }
            cur.insert(a[i]);
            ans.insert(a[i]);
            pre.swap(cur);
        }
        
        LL t = 1;
        while (ans.count(t)) t ++ ;
        cout << t << endl;
    }
    return 0;
}

还是没搞懂为什么INF取1e9，之后再补