0-1规划下的数独问题

news2025/2/23 5:35:33
  • 数独显然是一个0-1规划问题.
  • 虽然这个什么凸分析还是啥的分析有这个优化的方法,但是,你DFS也不是完全一点不可能的对吧.
  • 嗯,既然这样的话,我们就要去解决这样一个更细致的问题了.数独这个问题他的解的存在性,唯一性怎么样.
  • 当然,已经有结论了,一个9*9的数独至少要给出17个值才能约束出一个唯一确定的解
  • 我们的目的是什么呢?
  • 嗯,好问题,实在不行就调研吧......
    • 16个条件时,解的多样性等等等
  • 论文已经给出了,我们要做的事情就是先写一点点代码.

Lingo解决数独问题

model:

sets:
number/1..9/;
line/1..9/;
col/1..9/;
link(line,col,number):x;
endsets

data:

@text("ans.txt")=x;
enddata

x(1,1,1) = 1;
x(1,6,7) = 1;
x(1,8,9) = 1;

x(2,2,3) = 1;
x(2,5,2) = 1;
x(2,9,8) = 1;

x(3,3,9) = 1;
x(3,4,6) = 1;
x(3,7,5) = 1;

x(4,3,5) = 1;
x(4,4,3) = 1;
x(4,7,9) = 1;

x(5,2,1) = 1;
x(5,5,8) = 1;
x(5,9,2) = 1;

x(6,6,4) = 1;

x(7,1,3) = 1;
x(7,8,1) = 1;

x(8,2,4) = 1;
x(8,9,7) = 1;

x(9,3,7) = 1;
x(9,7,3) = 1;




@for(line(i):@for(col(j):@sum(number(k):x(i,j,k))=1));

@for(line(i):@for(number(k):@sum(col(j):x(i,j,k))=1));

@for(col(j):@for(number(k):@sum(line(i):x(i,j,k))=1));

@for(number(k):@sum(line(i)|i#GE#1#and#i#LE#3:@sum(col(j)|j#GE#1#and#j#LE#3:x(i,j,k)))=1);
@for(number(k):@sum(line(i)|i#GE#1#and#i#LE#3:@sum(col(j)|j#GE#4#and#j#LE#6:x(i,j,k)))=1);
@for(number(k):@sum(line(i)|i#GE#1#and#i#LE#3:@sum(col(j)|j#GE#7#and#j#LE#9:x(i,j,k)))=1);

@for(number(k):@sum(line(i)|i#GE#4#and#i#LE#6:@sum(col(j)|j#GE#1#and#j#LE#3:x(i,j,k)))=1);
@for(number(k):@sum(line(i)|i#GE#4#and#i#LE#6:@sum(col(j)|j#GE#4#and#j#LE#6:x(i,j,k)))=1);
@for(number(k):@sum(line(i)|i#GE#4#and#i#LE#6:@sum(col(j)|j#GE#7#and#j#LE#9:x(i,j,k)))=1);

@for(number(k):@sum(line(i)|i#GE#7#and#i#LE#9:@sum(col(j)|j#GE#1#and#j#LE#3:x(i,j,k)))=1);
@for(number(k):@sum(line(i)|i#GE#7#and#i#LE#9:@sum(col(j)|j#GE#4#and#j#LE#6:x(i,j,k)))=1);
@for(number(k):@sum(line(i)|i#GE#7#and#i#LE#9:@sum(col(j)|j#GE#7#and#j#LE#9:x(i,j,k)))=1);

@for(link(i,j,k):@bin(x(i,j,k)));
end

读取与验证


f = open("ans.txt")
F = f.readlines()
F = [int(F[i].split(" ")[-1][0]) for i in range(729)]

def check(result):
    flag = 1
    for i in range(9):
        flag = (len(set([result[i*9+j] for j in range(9)])) == 9)
        if not flag:
            print("第"+str(i+1)+"行不满足条件")
            return False
        
    for i in range(9):
        flag = (len(set([result[i+9*j] for j in range(9)])) == 9)
        if not flag:
            print("第"+str(j+1)+"列不满足条件")
            return False
        
    for k in range(3):
        for l in range(3):
            block = ""
            for i in range(3):
                for j in range(3):
                    block += result[9*(3*k+i)+(3*l+j)]
            flag = (len(set(block)) == 9)

            if not flag:
                print("("+str(k+1)+","+str(l+1)+")"+"个块不满足条件")
                return False
    return True

count = 0
result,result0 = "",""
for i in range(81): 
    for j in range(9):
        if F[i*9+j] == 1:
            result += (str(j+1))

assert(len(result)==81),"结果总数不是81个"
##result = list(result)
##result[9] = 1
##r = ""
##for i in result:
##    r += str(i)
##result = r
if check(result):
    for i in range(9):
        result0 += (result[i*9:(1+i)*9]+"\n")
print(result0)

C++ DFS

  • 显然，我们不想看到我们只能用 Lingo 这样不太方便的方法。
  • 我们用深度优先简单的搜索一下这个数独问题的答案
#include<iostream>
#include<fstream>

using namespace std;
typedef int Board[9][9];
int count=0;
void initial(Board board);
void output(Board board);
bool completed(Board board);
bool check(Board board,int i,int j,int target);
void solve(Board board);
ofstream ans("answer.txt");

int main()
{
	ans.open("answer.txt",ios::out);
	ans << "all answer!";
	ans.close();
	Board board;
	initial(board);
	solve(board);
	if (!completed(board))
	{
		cout << "the number of solutions:";
		cout << count << endl;
	}
	return 0;

}


void initial(Board board)
{
	board[0][0] = 1;
	board[0][1] = 2;
	board[0][2] = 0;
	board[0][3] = 5;
	board[0][4] = 0;
	board[0][5] = 0;
	board[0][6] = 0;
	board[0][7] = 0;
	board[0][8]	= 0;

	board[1][0] = 0;
	board[1][1] = 0;
	board[1][2] = 0;	
	board[1][3] = 0;
	board[1][4] = 9;
	board[1][5] = 0;
	board[1][6] = 2;
	board[1][7] = 0;
	board[1][8]	= 0;
	
	board[2][0] = 0;
	board[2][1] = 5;
	board[2][2] = 0;
	board[2][3] = 0;
	board[2][4] = 0;
	board[2][5] = 2;
	board[2][6] = 0;
	board[2][7] = 0;
	board[2][8]	= 0;
	
	board[3][0] = 7;
	board[3][1] = 0;
	board[3][2] = 5;
	board[3][3] = 0;
	board[3][4] = 0;
	board[3][5] = 0;
	board[3][6] = 0;
	board[3][7] = 0;
	board[3][8]	= 9;
	
	board[4][0] = 0;
	board[4][1] = 4;
	board[4][2] = 0;
	board[4][3] = 0;
	board[4][4] = 0;
	board[4][5] = 0;
	board[4][6] = 0;
	board[4][7] = 2;
	board[4][8]	= 0;
	
	board[5][0] = 6;
	board[5][1] = 0;
	board[5][2] = 0;
	board[5][3] = 0;
	board[5][4] = 0;
	board[5][5] = 0;
	board[5][6] = 0;
	board[5][7] = 0;
	board[5][8]	= 0;
	
	board[6][0] = 0;
	board[6][1] = 0;
	board[6][2] = 0;
	board[6][3] = 2;
	board[6][4] = 0;
	board[6][5] = 0;
	board[6][6] = 0;
	board[6][7] = 1;
	board[6][8]	= 0;
	
	board[7][0] = 0;
	board[7][1] = 0;
	board[7][2] = 8;
	board[7][3] = 0;
	board[7][4] = 4;
	board[7][5] = 0;
	board[7][6] = 0;
	board[7][7] = 3;
	board[7][8]	= 0;
	
	board[8][0] = 0;
	board[8][1] = 0;
	board[8][2] = 0;
	board[8][3] = 7;
	board[8][4] = 0;
	board[8][5] = 1;
	board[8][6] = 6;
	board[8][7] = 0;
	board[8][8]	= 4;
}

void output(Board board)
{
	cout << "============\n";
	
	ans.open("answer.txt",ios::app);
	for(int i=0;i<9;i++)
	{
		for(int j=0;j<9;j++)
		{
			ans << board[i][j];
		}
	}
	ans << "\n";
	ans.close();
	
	for(int i=0;i<9;i++)
	{
		for(int j=0;j<9;j++)
		{
			cout << board[i][j] << " ";
		}
		cout << endl;
	}
}

bool completed(Board board)
{
	for(int i=0;i<9;i++)
	{
		for(int j=0;j<9;j++)
		{
			if(board[i][j]==0)
			{
				return false;
			}
		}
	}
	return true;
}

bool check(Board board,int i,int j,int target)
{
	//行，列检验
	for (int m=0;m<9;m++)
	{
		if(board[i][m]==target || board[m][j]==target)
		{
			return false;
		}
	}
	
	//block 检验
	int x0 = (i/3)*3,y0 = (j/3)*3;
	for(int p=0;p<3;p++)
	{
		for (int q=0;q<3;q++)
		{
			if (board[x0+p][y0+q]==target)
			{
				return false;
			}
		}
	}
	return true;	
}

void solve(Board board)
{
	for(int i=0;i<9;i++)
	{
		for(int j=0;j<9;j++)
		{
			if(board[i][j]==0)
			{
				for(int k=1;k<10;k++)
				{
					if (check(board,i,j,k))
					{
						board[i][j] = k;
						solve(board);
						if (completed(board))
						{
							output(board);
							count++;
						}
						board[i][j] = 0;
					}
				}
				return ;	
				//只要从一个0元素开始即可，没必要再来一次。
				//解的相对唯一性还是啥的。
			}
		}
	}
}

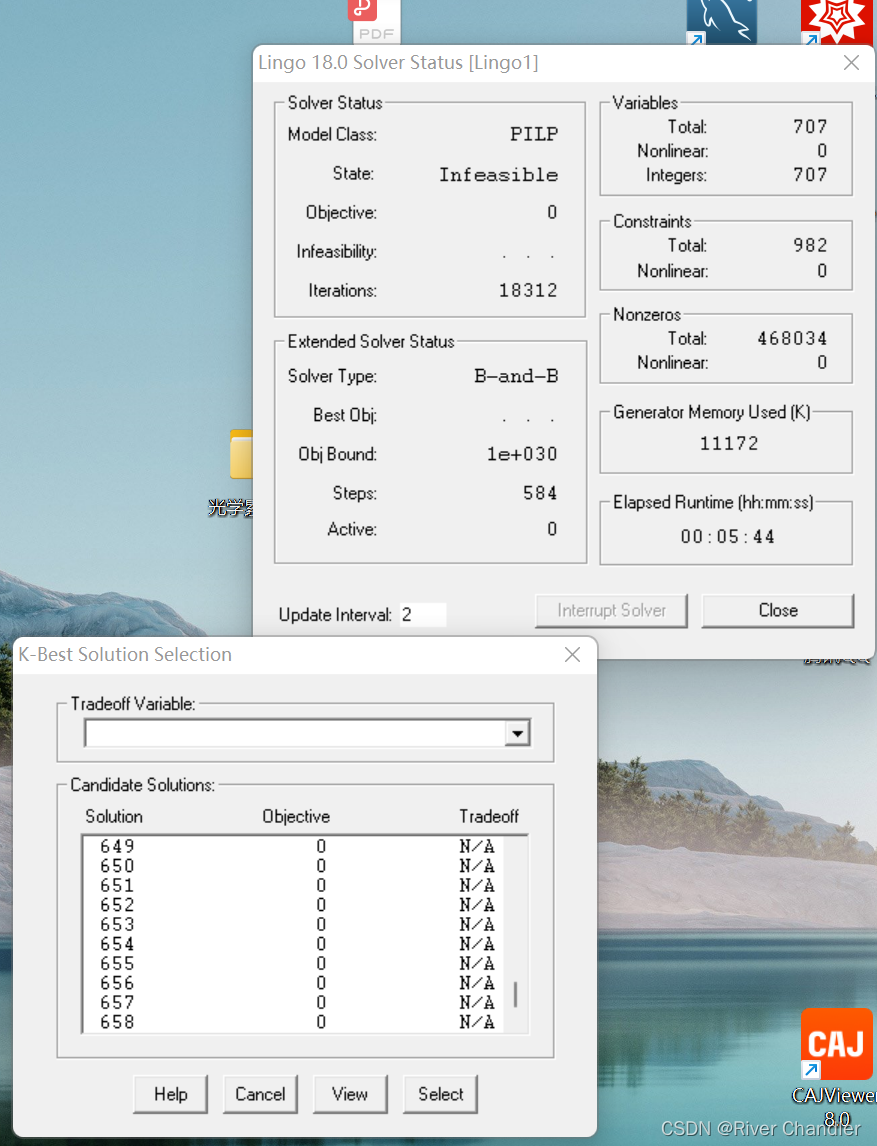
 至少总结一点吧：Lingo也没有那么快，有的时候。。

大型线性稀疏系统

数独很明显是一个大型的线性稀疏系统，我们怎么解一个大型线性稀疏系统呢？

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/91289.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Qt扫盲-QGridLayout理论总结

Qt扫盲-QGridLayout理论总结

QGridLayout理论总结1. 简介2. 操作布局元素3. 常用属性4. 间隔设置1. 简介 QGridLayout 占用来自其父布局或 parentWidget()获得的空间&#xff0c;将其划分为行列表格形式&#xff0c;在每个布局的表格里放置控件或者布局器就行。 一般来说&#xff0c;列和行的行为功能相同…
阅读更多...
Sourcetree安装详细步骤

Sourcetree安装详细步骤

前言&#xff1a; Sourxetree 作为 免费的 Git 客户端工具&#xff0c;有许多优点。Sourcetree 简化了与Git存储库交互的方式&#xff0c;因此我们可以专注于编码。通过 Sourcetree 简单又快捷的管理我们 的存储库。 下载安装包 进入 官网 选择Windows系统的安装包 &#xff…
阅读更多...
【大数据技术Hadoop+Spark】HDFS Shell常用命令及HDFS Java API详解及实战（超详细 附源码）

【大数据技术Hadoop+Spark】HDFS Shell常用命令及HDFS Java API详解及实战（超详细 附源码）

需要源码请点赞关注收藏后评论区留言私信~~~ 一、HDFS的Shell介绍 Shell在计算机科学中俗称“壳”&#xff0c;是提供给使用者使用界面的进行与系统交互的软件&#xff0c;通过接收用户输入的命令执行相应的操作&#xff0c;Shell分为图形界面Shell和命令行式Shell。 文件系统…
阅读更多...
PTC Creo Illustrate生产技术设备

PTC Creo Illustrate生产技术设备

PTC Creo Illustrate生产技术设备 Creo Illustrator是一款适用于生产技术设备的软件。该软件将三种功能与当前CAD设计数据、技术规范以及所需和可能使用的各种部件相结合。这些工具对供应商和客户尤其有用。供应商可以使用本文档中提供的信息熟悉机器。查看内部零件&#xff0c…
阅读更多...
YOLO系列目标检测算法——YOLOR

YOLO系列目标检测算法——YOLOR

YOLO系列目标检测算法目录 - 文章链接 YOLO系列目标检测算法总结对比- 文章链接 YOLOv1- 文章链接 YOLOv2- 文章链接 YOLOv3- 文章链接 YOLOv4- 文章链接 Scaled-YOLOv4- 文章链接 YOLOv5- 文章链接 YOLOv6- 文章链接 YOLOv7- 文章链接 PP-YOLO- 文章链接 …
阅读更多...
喜讯 | 美格智能子公司美格智联成功获选2022年首批国家级“高新技术企业”认定

喜讯 | 美格智能子公司美格智联成功获选2022年首批国家级“高新技术企业”认定

近日&#xff0c;全国高新技术企业认定管理工作领导小组办公室发布了关于对深圳市认定机构2022年认定的第一批高新技术企业进行备案公示的通知&#xff0c;根据《高新技术企业认定管理办法》&#xff08;国科发火〔2016〕32号&#xff09;和《高新技术企业认定管理工作指引》&a…
阅读更多...
[C/C++/初学者]500以内的亲密数对（VS2012）

[C/C++/初学者]500以内的亲密数对（VS2012）

在开始编写程序之前&#xff0c;我们需要了解一个东西。 何为亲密数对&#xff1f; 简单来说&#xff0c;就是数a的正因子数&#xff08;除本身外&#xff09;等于数b的正因子数&#xff08;除本身外&#xff09;。 符合这项条件的两个数&#xff0c;我们称他们为亲密数对。 …
阅读更多...
[附源码]Python计算机毕业设计高校体育馆管理信息系统Django（程序+LW）

[附源码]Python计算机毕业设计高校体育馆管理信息系统Django（程序+LW）

该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程 项目运行 环境配置&#xff1a; Pychram社区版 python3.7.7 Mysql5.7 HBuilderXlist pipNavicat11Djangonodejs。 项目技术&#xff1a; django python Vue 等等组成&#xff0c;B/S模式 pychram管理等…
阅读更多...
146.个性化推荐系统案例介绍

146.个性化推荐系统案例介绍

YouTube的推荐系统算法由两个神经网络组成&#xff1a; 一个用于候选生成一个用于排序 以用户的浏览历史为输入&#xff0c;候选生成网络可以显著减小可推荐的视频数量&#xff0c;从庞大的库中选出一组最相关的视频 这样生成的候选视频与用户的相关性最高&#xff0c;然后会对…
阅读更多...
【ROS话题通信】发布者和订阅者

【ROS话题通信】发布者和订阅者

前言 本文记录ROS话题通信的学习过程&#xff0c;便于后续复习。首先明确&#xff0c;ROS中的话题通信&#xff0c;在ROS通信中非常重要&#xff0c;实现了分布式发布接收消息&#xff0c;也是实现了不同编程语言间的解耦&#xff0c;下面记录下自己学习过程中的相关代码和配置…
阅读更多...
Kotlin小菜——基础语言教程

Kotlin小菜——基础语言教程

概述 Kotlin是JetBrains推出的一种编程语言&#xff0c;JetBrains是最智能的Java IDE的官方设计器&#xff0c;名为Intellij IDEA。这是在JVM上运行的强静态类型语言。2017年&#xff0c;谷歌宣布Kotlin是Android开发的官方语言。Kotlin是一种开源编程语言&#xff0c;它将面向…
阅读更多...
会话Cookie跟踪技术

会话Cookie跟踪技术

会话 用户打开浏览器&#xff0c;访问web服务器的资源&#xff0c;会话建立&#xff0c;直到有一方断开连接&#xff0c;会话结束。在一次会话中可以包含多次请求和响应。 从浏览器发出请求到服务端响应数据给前端之后&#xff0c;一次会话(在浏览器和服务器之间)就被建立了 …
阅读更多...
产品设计：Material Design 学习笔记二

产品设计：Material Design 学习笔记二

​5、图标 桌面图标 桌面图标尺寸是48dp X 48dp。 桌面图标建议模仿现实中的折纸效果&#xff0c;通过扁平色彩表现空间和光影。注意避免以下问题&#xff1a; ①不要给彩色元素加投影 ②层叠不要超过两层 ③折角不要放在左上角 ④带投影的元素要完整展现&#xff0c;不能…
阅读更多...
Debug怎么用

Debug怎么用

文章目录前言一、打断点运行Debug二、页面重新运行功能三、回到代码看断点前言 提示&#xff1a;这里可以添加本文要记录的大概内容&#xff1a; 因为最近有个项目注册不好使&#xff0c;想看看哪的问题&#xff0c;所以用debug看看程序走到了哪 提示&#xff1a;以下是本篇文…
阅读更多...
docker部署mysql初始化数据库

docker部署mysql初始化数据库

一、前言 在使用docker部署mysql服务时&#xff0c;往往需要在创建容器时新建database&#xff0c;在需要在创建实例的过程中希望初始化sql脚本。 mysql官方镜像支持在容器初次启动时自动执行指定的sql脚本或shell脚本&#xff08;注意&#xff1a;只有初次启动时才能自动执行&…
阅读更多...
【正点原子I.MX6U-MINI】通过tftp从Ubuntu中下载zImage 和设备树文件 | 从网络启动Linux系统

【正点原子I.MX6U-MINI】通过tftp从Ubuntu中下载zImage 和设备树文件 | 从网络启动Linux系统

从网络启动linux系统的唯一目的就是为了调试&#xff01;不管是为了调试linux系统还是linux下的驱动。每次修改linux系统文件或者linux下的某个驱动以后都要将其烧写到EMMC中去测试&#xff0c;这样太麻烦了。我们可以设置linux从网络启动&#xff0c;也就是将 linux 镜像文件和…
阅读更多...
【OpenCV-Python】教程：5-3 光流

【OpenCV-Python】教程：5-3 光流

OpenCV Python Optical Flow (光流) 【目标】 了解光流的概念和用 Lucas-Kanade 算法估计光流我们将使用cv2.calcOpticalFlowPyrLK()这样的函数来跟踪视频中的特征点。们将使用cv2.calcOpticalFlowFarneback()方法创建一个密集的光流场&#xff0c;可以用于前景检测。 【理论…
阅读更多...
[附源码]Python计算机毕业设计高校心理咨询管理系统Django（程序+LW）

[附源码]Python计算机毕业设计高校心理咨询管理系统Django（程序+LW）

该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程 项目运行 环境配置&#xff1a; Pychram社区版 python3.7.7 Mysql5.7 HBuilderXlist pipNavicat11Djangonodejs。 项目技术&#xff1a; django python Vue 等等组成&#xff0c;B/S模式 pychram管理等…
阅读更多...
Java+SSH实验室预约系统(含源码+论文+答辩PPT等)

Java+SSH实验室预约系统(含源码+论文+答辩PPT等)

该项目采用技术&#xff1a; 后台&#xff1a;SpringSpringmvcHibernate 前台JqueryMy97DatePickercssjs 使用了MySQLTomcat等相关技术 项目含有源码、文档、配套开发软件、软件安装教程、项目发布教程等 本系统的用户可以分为三种&#xff1a;管理员、教师、学生。以下针对三种…
阅读更多...
协同共进 | 中睿天下入会工业信息安全产业发展联盟

协同共进 | 中睿天下入会工业信息安全产业发展联盟

近日&#xff0c;中睿天下加入“工业信息安全产业发展联盟”&#xff0c;成为新一批会员单位。 工业信息安全是网络安全、国家安全的重要组成部分&#xff0c;涉及工业领域各个环节,涵盖工业控制系统安全、工业互联网安全、工业数据安全等各领域&#xff0c;直接关系到经济发展…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023