在开始编写程序之前，我们需要了解一个东西。

何为亲密数对？

简单来说，就是数a的正因子数（除本身外）等于数b的正因子数（除本身外）。

符合这项条件的两个数，我们称他们为亲密数对。

那么，既然规则已经知晓，那么接下来就开始实操了。

---

首先我们需要两个for循环，用于判断两个数之间的关系，我们需要定义两个int型变量，

又因为我们需要判断正因子数之和与其本身的关系，我们又需要定义两个int型变量。

所以我们一共需要定义四个int型变量。

以下为定义变量：

int i,j,a=0,b=0;

printf("500以内的所有亲密数如下所示:\n");

以下为for的循环嵌套结构：

for (i=1;i<=500;i++)
	{
		for (j=1;j<=500;j++) 
		{
           ...
		}
	}

在for循环里，我们需要完成以下步骤：

1. 判断两个数是否相同，因为亲密数对不可为两个相同的数。
2. 判断正因子数是否相同，这里就需要计算正因字子数的和，并需要对两个数的正因子数的和进行判断了。
3. 判断此前是否已经有类似的答案，比如：220和280是亲密数对，那我们后面能再说280和220是亲密数对嘛？这不是一种情况嘛？故我们需要排除这种类似的答案。

            //若两个数相同，则退出本层循环
            if (i==j)
                continue;

            //判断正因子数是否相同
            if (Sum(i)==j&&i==Sum(j)) 
            {
                
                //判断是否存在此前已经有相同答案的情况，若有，则跳出
                if (j==a&&i==b)
                {
                    continue;
                }
                

                //若符合相应条件，则输出对应数据

                printf("%4d和%4d为亲密对数\n", i, j);
                
                //m，n记录符合条件的数据。
                a=i;
                b=j;
                
            }

因为需要拿正因子数的和与本身作比较，所以我们需要一个代码块来实现他，但由于题目中要求我们体现函数的应用，故我们把这段单独拿出作为一个函数。

我们可以使用一个for循环来递归，用if来判断谁是他的正因子，并通过一个变量将这些数据保存下来，最终返回主函数进行判断。

以下为记录正因子数和的代码：

//记录正因字的和
int Sum(int n) 
{
	int m=0, sum=0;
	for (m=1;m<n;m++)
	{
		//判断n的正因子数，并将它们的和保存下来
		if (n%m==0) 
		{
			sum=sum+m;
		}
	}
	return sum;
}

以下为完整代码：

#include <stdio.h>

//记录正因字的和
int Sum(int n) 
{
	int m=0, sum=0;
	for (m=1;m<n;m++)
	{
		//判断n的正因子数，并将它们的和保存下来
		if (n%m==0) 
		{
			sum=sum+m;
		}
	}
	return sum;
}

int main()
{
	int i,j,a=0,b=0;

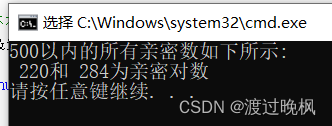
	printf("500以内的所有亲密数如下所示:\n");

	for (i=1;i<=500;i++)
	{
		for (j=1;j<=500;j++) 
		{
			//若两个数相同，则退出本层循环
			if (i==j)
				continue;

			//判断正因子数是否相同
			if (Sum(i)==j&&i==Sum(j)) 
			{
				
				//判断是否存在此前已经有相同答案的情况，若有，则跳出
				if (j==a&&i==b)
				{
					continue;
				}

				printf("%4d和%4d为亲密对数\n", i, j);
				
				//m，n记录符合条件的数据。
				a=i;
				b=j;
				
			}
		}
	}
}

执行结果如下：