刷题顺序及思路来源于代码随想录,网站地址:https://programmercarl.com
目录
617. 合并二叉树
700. 二叉搜索树中的搜索
98. 验证二叉搜索树
530. 二叉搜索树的最小绝对差
501. 二叉搜索树中的众数
617. 合并二叉树
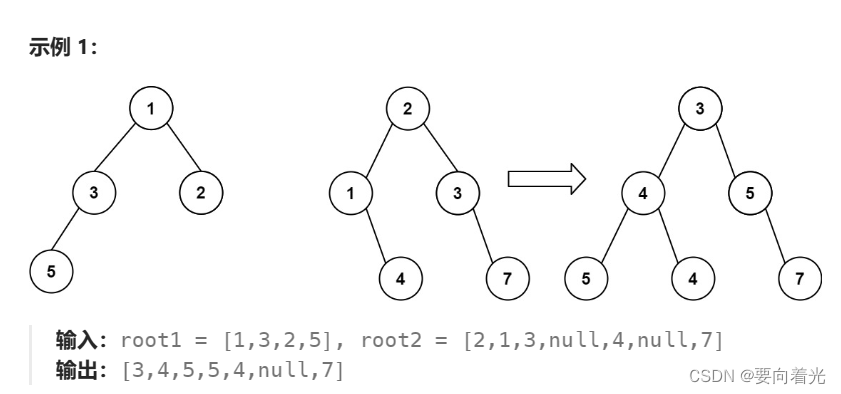
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if(root1==null){
return root2;
}
if(root2==null){
return root1;
}
root1.val+= root2.val;
root1.left=mergeTrees(root1.left,root2.left);
root1.right=mergeTrees(root1.right,root2.right);
return root1;
}
}700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。

/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if(root==null||root.val==val){
return root;
}
TreeNode result=null;
if(root.val>val){
result=searchBST(root.left,val);
}
if(root.val<val){
result=searchBST(root.right,val);
}
return result;
}
}98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。

/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*
*(思路:利用特性,中序遍历的时候元素是有序的
* 定义一个指针,始终指向root的前一个节点,中序遍历时,若pre>=root.val;
* 则说明二叉树不是搜索二叉树
*/
class Solution {
TreeNode pre=null;
public boolean isValidBST(TreeNode root) {
if(root==null){
return true;
}
//中序遍历:左
boolean left=isValidBST(root.left);
//中序遍历:中
if(pre!=null&&pre.val>=root.val){
return false;
}
pre=root;
//中序遍历:右
boolean right=isValidBST(root.right);
return left&&right;
}
}530. 二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。

/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
* (思路:利用二叉搜索树特性,自我理解:在中序遍历中,二叉树遍历出来是有序数组,
* 求任意两节点间最小差值就是求遍历过程中相邻两节点的差值的最小值;
*/
class Solution {
TreeNode pre=null; //记录上一个节点
int result=Integer.MAX_VALUE; //记录最小差值
public int getMinimumDifference(TreeNode root) {
if(root==null){
return 0;
}
traversal(root);
return result;
}
private void traversal(TreeNode root) {
if(root==null){
return;
}
//中序遍历:左
traversal(root.left);
//中序遍历:中
if(pre!=null){
result=Math.min(result,root.val-pre.val);
}
pre=root;
//中序遍历:右
traversal(root.right);
}
}501. 二叉搜索树中的众数
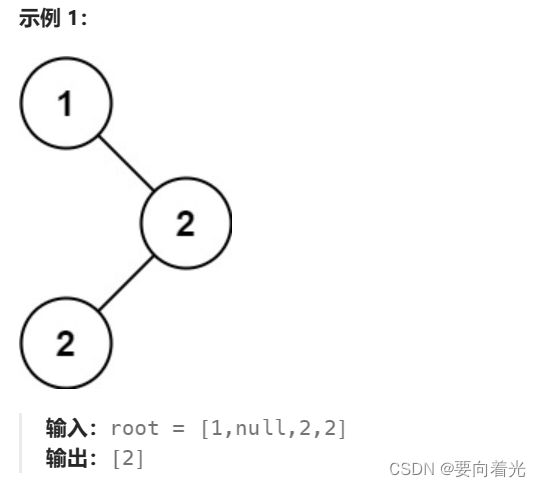
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> list=new ArrayList<>();
TreeNode pre=null;
int count=0;
int maxCount=0;
public int[] findMode(TreeNode root) {
findMax(root);
int[] res=new int[list.size()];
for (int i = 0; i < list.size(); i++) {
res[i]= list.get(i);
}
return res;
}
private void findMax(TreeNode root) {
if(root==null){
return;
}
findMax(root.left); //左
if(pre==null){
count=1;
} else if (pre.val==root.val) {
count++;
}else {
count=1;
}
pre=root;
if(count==maxCount){
list.add(root.val);
} else if (count>maxCount) {
maxCount=count;
list.clear();
list.add(root.val);
}
findMax(root.right);
}
}