公式太多了,就用图片用笔记呈现,SVM虽然算法本质一目了然,但其中用到的数学推导还是挺多的,其中拉格朗日约束关于α>0这块证明我看了很长时间,到底是因为悟性不够。对偶问题也是,用了一个简单的例子才明白,事实上,从简单的例子进行来理解更复杂的东西确实很舒服。核函数这块主要是正定核函数的证明需要看一下,K(x.z)=I(x)*I(z),先升维再求点积=先点积再升维。最后SMO,经典中的经典,看的我头疼,最主要的就是公式的推导。

















代码:
'''
原理解释:
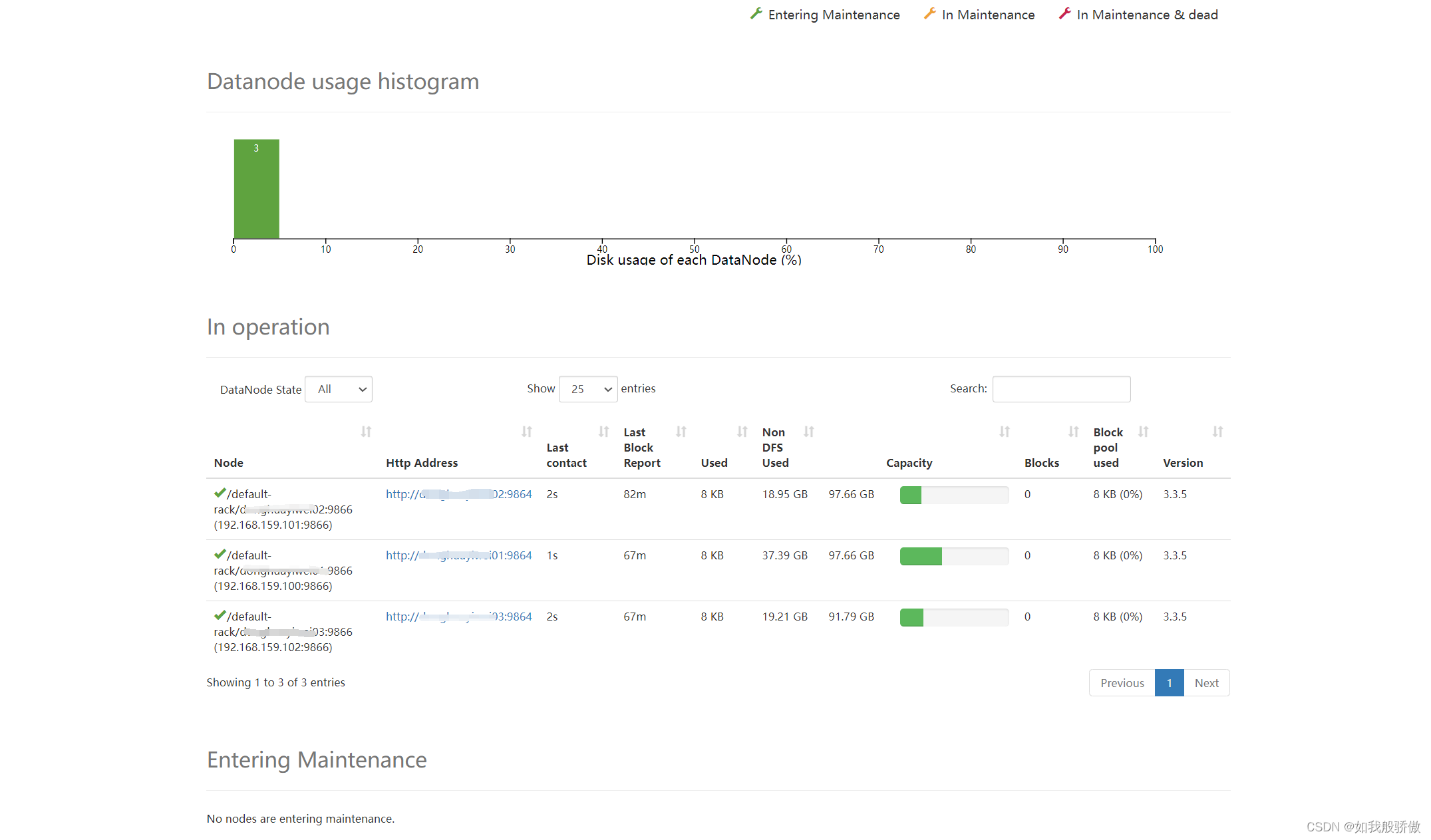
支持向量为距离超平面最近的一个向量
而我们要寻找的是支持向量到超平面的最大距离
超平面可定义为W^T x +b=0 (参照二维直线方程ax+by+c=0)
二维空间点(x,y)到直线Ax+By+C=0的距离公式是:
|Ax+By+C|/(A^2+B^2)^(1/2)
扩展到n维空间后,点x=(x1,x2,x3,,,xn)到直线W^T x+b=0的距离为:
|W^T x+b|/||w||
其中||W||=(w1^2+...wn^2)^(1/2)
因为支持向量到超平面的距离是d,也是样本点到超平面的最短距离
所以
(W^T x+b)/||W||>=d,y=1
(W^T X+b)/||W||<=-d,y=-1
稍作转换可以得到:
(W^T x+b)/(||W||*d)>=1,y=1
(W^T X+b)/(||W||*d)<=-1,y=-1
'''
from __future__ import print_function
from numpy import *
import matplotlib.pyplot as plt
class optStruct:
'''
建立的数据结构来保存所有的重要值
'''
def __init__(self,dataMatIn,classLabels,C,toler,kTup):
'''
Args:
dataMatIn 数据集
classLabels 类别标签
C 松弛变量(常量值),允许有些数据点可以处于分割面的错误一侧
控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重
可以通过调节该参数达到不同的结果
toler 容错率
kTup 包含核函数信息的元组
'''
self.X=dataMatIn
self.labelMat=classLabels
self.C=C
self.tol=toler
#数据的行数
self.m=shape(dataMatIn)[0]
self.alphas=mat(zeros((self.m,1)))
self.b=0
#误差缓存,第一列给出的是eCache是否有效的标志位,第二列给出的是实际的E值
self.eCache=mat(zeros((self.m,2)))
#m行m列的矩阵
#m行m列的矩阵
self.K=mat(zeros((self.m,self.m)))
for i in range(self.m):
self.K[:,i]=kernelTrans(self.X,self.X[i,:],kTup)
def kernelTrans(X,A,kTup):# calc the kernel or transform data to a higher dimensional space
"""
核转换函数
Args:
X dataMatIn数据集
A dataMatIn数据集的第i行的数据
kTup 核函数的信息
Returns:
"""
m,n=shape(X)
K=mat(zeros((m,1)))
if kTup[0]=='lin':
#linear kernel: m*n * n*1=m*1
K=X*A.T
elif kTup[0]=='rbf':
for j in range(m):
deltaRow=X[j,:]-A
K[j]=deltaRow*deltaRow.T
#径向基函数的高斯版本
K=exp(K/(-1*kTup[1]**2))#divide in numpy is element-wise not matrix like matlab
else:
raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
return K
def loadDataSet(fileName):
'''
loadDataSet(对文件进行逐行解析,从而得到第n行的类标签和整个数据矩阵)
Args:
fileName 文件名
Returns:
dataMat 数据矩阵
labelMat 类标签
'''
dataMat = []
labelMat=[]
fr=open(fileName)
for line in fr.readlines():
lineArr=line.strip().split('\t')
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
def calcEk(oS,k):
'''
calcEk(求Ek误差:预测值-真实值的差)
该过程在完整版的SMO算法中出现的次数较多,因此将其单独作为一个方法
Args:
oS optStruct对象
k 具体的某一行
Returns:
Ek 预测结果与真实结果比对,计算误差Ek
'''
fXk=float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k]+oS.b) #E=apha*y*k+b-g(x)
Ek=fXk-float(oS.labelMat[k])
return Ek
def selectJrand(i,m):
'''
随机选择一个整数
Args:
i 第一个alpha的下标
m 所有alpha的数目
Returns:
j 返回一个不为i的随机数,在0~m之间的整数值
'''
j=i
while j==i:
j=int(random.uniform(0,m))
return j
def selectJ(i,oS,Ei): #this is the second choice -heurstic,and calcs Ej
'''
内循环的启发式方法
选择第二个(内循环)alpha的alpha值
这里的目标是选择合适的第二个alpha值以保证每次优化中采用的最大步长
该函数的误差与第一个alpha值Ei和下标i有关
Args:
i 具体的第一行
oS optStruct对象
Ei 预测结果与真实性结果比对,计算误差Ei
Returns:
j 随机选出的第j一行
Ej 预测结果与真实结果比对,计算误差Ej
'''
maxK=-1
maxDeltaE=0
Ej=0
#首先将输入值Ei在缓存中设置成为有效的,这里的有效意味着它已经计算好了
oS.eCache[i]=[1,Ei]
# print ('oS.ecache[%s]=%s' %(i,oS.eCache[i]))
#print ('oS.eCache[:,0].A=%s'%oS.eCache[:,0].A.T)
#
##返回非0的:行列值
# nonzero(oS.eCache[:,0].A)=(
# 行: array([ 0, 2, 4, 5, 8, 10, 17, 18, 20, 21, 23, 25, 26, 29, 30, 39, 46,52, 54, 55, 62, 69, 70, 76, 79, 82, 94, 97]),
# 列: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0])
#)
# print('nonzero(oS.eCache[:,0].A)=',nonzero(oS.eCache[:,0].A))
# # 取行的list
# print('nonzero(oS.eCache[:,0].A)[0]=',nonzero(oS.eCache[:,0].A)[0])
# 非零E值的行的list列表,所对应的alpha值
validEcacheList=nonzero(oS.eCache[:,0].A)[0]
if(len(validEcacheList))>1:
for k in validEcacheList: #在所有的值上进行循环,并选择其中使得改变最大的那个值
if k==i:
continue #don't calc for i,waste of time
#求Ek误差: 预测值-真实值的差
Ek=calcEk(oS,k)
deltaE=abs(Ei-Ek)
if(deltaE>maxDeltaE):
#选择具有最大步长的j
maxK=k
maxDeltaE=deltaE
Ej=Ek
return maxK,Ej
else: #如果是第一次循环,则随机选择一个alpha值
j=selectJrand(i,oS.m)
#求Ek误差:预测值-真实值的差
Ej=calcEk(oS,j)
return j,Ej
def updateEk(oS,k):
"""updateEk(计算误差值并存入缓存中。)
在对alpha值进行优化之后会用到这个值。
Args:
oS optStruct对象
k 某一列的行号
"""
# 求 误差: 预测值-真实值的差
Ek=calcEk(oS,k)
oS.eCache[k]=[1,Ek]
def clipAlpha(aj,H,L):
'''
clipAlpha(调整aj的值,使aj处于 L<=aj<=H)
Args:
aj 目标值
H 最大值
L 最小值
Returns:
aj 目标值
'''
if aj>H:
aj=H
if L>aj:
aj=L
return aj
def innerL(i,oS):
'''
innerL
内循环代码
Args:
i 具体的某一行
oS optStruct对象
Returns:
0 找不到最优的值
1 找到了最优的值,并且oS.Cache到缓存中
'''
# 求Ek误差:预测值-真实值的差
Ei=calcEk(oS,i)
# 约束条件(KKT条件是解决最优化问题时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值)
# 0<=alphas[i]<=C,但由于0和C是边界值,我们无法进行优化,因为需要增加一个alphas和降低一个alphas
# 表示发生错误的概率:labelMat[i]*Ei 如果超出了toler,才需要优化,至于正负号,我们考虑绝对值就对了
'''
# 检验训练样本(xi, yi)是否满足KKT条件
yi*f(i) >= 1 and alpha = 0 (outside the boundary)
yi*f(i) == 1 and 0<alpha< C (on the boundary)
yi*f(i) <= 1 and alpha = C (between the boundary)
'''
if((oS.labelMat[i]*Ei<-oS.tol)and (oS.alphas[i]<oS.C)) or ((oS.labelMat[i]*Ei>oS.tol) and (oS.alphas[i]>0)):
#选择最大的误差对应的j进行优化,效果更明显
j,Ej=selectJ(i,oS,Ei)
alphaIold=oS.alphas[i].copy()
alphaJold=oS.alphas[j].copy()
#L和H用于将alphas[j]调整到0-C之间,如果L==H,就不做任何改变,直接return 0
if(oS.labelMat[i]!=oS.labelMat[j]):
L=max(0,oS.alphas[j]-oS.alphas[i])
H=min(oS.C,oS.C+oS.alphas[j]-oS.alphas[i])
else:
L=max(0,oS.alphas[i]+oS.alphas[j]-oS.C)
H=min(oS.C,oS.alphas[j]+oS.alphas[i])
if L==H:
# print("L==H")
return 0
# eta是alphas[j]的最优修改量,如果eta==0,需要退出for循环的当前迭代过程
#参考《统计学习方法》李航-P125~P128<序列最小最优化算法>
eta=2.0*oS.K[i,j]-oS.K[i,i]-oS.K[j,j] #changed for kernel
if eta>=0:
print("eta>=0")
return 0
#计算出一个新的alphas[j]值
oS.alphas[j]-=oS.labelMat[j]*(Ei-Ej)/eta
#并使用辅助函数,以及L和H对其进行调整
oS.alphas[j]=clipAlpha(oS.alphas[j],H,L)
#更新误差缓存
updateEk(oS,j)
# 检查alpha[j]是否只是轻微的改变,如果是的话,就退出for循环
if(abs(oS.alphas[j]-alphaJold)<0.00001):
# print("j not moving enough")
return 0
#然后alphas[i]和alphas[j]同样进行改变,虽然改变的大小不一样,但是改变的方向正好相反
oS.alphas[i]+=oS.labelMat[j]*oS.labelMat[i]*(alphaJold-oS.alphas[j])
#更新误差缓存
updateEk(oS,i)
# 在对alpha[i],alpha[j] 进行优化之后,给这两个alpha值设置一个常数b
# w= Σ[1~n] ai*yi*xi => b = yi- Σ[1~n] ai*yi(xi*xj)
# 所以:b1-b=(y1-y)- Σ[1~n] yi*(a1-a)*(xi*x1)
# 为什么减2遍?因为是减去Σ[1~n],正好2个变量i和j,所以减2遍
b1=oS.b-Ei-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i]-oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
b2=oS.b-Ej-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]-oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
if(0<oS.alphas[i])and (oS.C>oS.alphas[i]):
oS.b=b1
elif (0<oS.alphas[j])and (oS.C>oS.alphas[j]):
oS.b=b2
else:
oS.b=(b1+b2)/2.0
return 1
else:
return 0
def smoP(dataMatIn,classLabels,C,toler,maxIter,kTup=('lin',0)):
'''
完整SMO算法外循环,与smoSimple有些类似,但这里的循环退出条件更多一些
Args:
dataMatIn 数据集
classLabels 类别标签
C 松弛变量(常量值),允许有些数据点可以处于分隔面的错误一侧。
控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。
可以通过调节该参数达到不同的结果。
toler 容错率
maxIter 退出前最大的循环次数
kTup 包含核函数信息的元组
Returns:
b 模型的常量值
alphas 拉格朗日乘子
'''
# 创建一个optStruct 对象
oS=optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler,kTup)
iter=0
entireSet=True
alphaPairsChanged=0
# 循环遍历:循环maxIter次 并且(alphaPairsChanged存在可以改变 or所有行遍历一遍)
while(iter<maxIter) and ((alphaPairsChanged>0)or (entireSet)):
alphaPairsChanged=0
# 当entireSet=true or 非边界alpha对没有了:就开始寻找alpha对,然后决定是否要进行else。
if entireSet:
# 在数据集上遍历所有可能的alpha
for i in range(oS.m):
#是否存在alpha对,存在就+1
alphaPairsChanged+=innerL(i,oS)
# print("fullSet,iter: %d i:%d,pairs changed %d" %(iter,i,clphaPairsChanged))
iter+=1
#对已存在alpha对,选出非边界的alpha值,进行优化
else:
#遍历所有的非边界alpha值,也就是不在边界0或C上的值
nonBoundIs=nonzero((oS.alphas.A>0)*(oS.alphas.A<C))[0]
for i in nonBoundIs:
alphaPairsChanged+=innerL(i,oS)
# print("non-bound,iter:%d i:%d,pairs changed %d"%(iter,i,alphaPairsChanged))
iter+=1
# 如果找到alpha对,就优化非边界alpha值,否则,就重新进行寻找,如果寻找一遍 遍历所有的行还是没找到,就退出循环
if entireSet:
entireSet=False #toggle entire set loop
elif(alphaPairsChanged==0):
entireSet=True
print("iteration number: %d" % iter)
return oS.b,oS.alphas
def calcWs(alphas,dataArr,classLabels):
'''
基于alpha计算w值
Args:
alphas 拉格朗日乘子
dataArr feature数据集
classLabels 目标变量数据集
Returns:
wc 回归系数
'''
X=mat(dataArr)
labelMat=mat(classLabels).transpose()
m,n=shape(X)
w=zeros((n,1))
for i in range(m):
w+=multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
def testRbf(k1=1.3):
dataArr,labelArr=loadDataSet('6.SVM/testSetRBF.txt')
b,alphas=smoP(dataArr,labelArr,200,0.0001,10000,('rbf',k1))#C=200 important
datMat=mat(dataArr)
labelMat=mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd] # get matrix of only support vectors
labelSV=labelMat[svInd]
print("there are %d Support Vectors"% shape(sVs)[0])
m,n=shape(datMat)
errorCount=0
for i in range(m):
kernelEval=kernelTrans(sVs,datMat[i,:],('rbf',k1))
# 和这个svm-simple类似: fxi=float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T))+b
predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b
if sign(predict)!=sign(labelArr[i]):
errorCount+=1
print("the training error rate is : %f" %(float(errorCount)/m))
dataArr,labelArr=loadDataSet('6.SVM/testSetRBF2.txt')
errorCount=0
datMat=mat(dataArr)
labelMat=mat(labelArr).transpose()
m,n=shape(datMat)
for i in range(m):
kernelEval=kernelTrans(sVs,datMat[i,:],('rbf',k1))
predict=kernelEval.T*multiply(labelSV,alphas[svInd])+b #w=Σalpha*y*x y=w*x+b
if sign(predict)!=sign(labelArr[i]):
errorCount+=1
print("the test error rate is : %f"%(float(errorCount)/m))
ws=calcWs(alphas,dataArr,labelArr)
plotfig_SVM(dataArr,labelArr,ws,b,alphas)
def img2vector(filename):
returnVect=zeros((1,1024))
fr=open(filename)
for i in range(32):
lineStr=fr.readline()
for j in range(32):
returnVect[0,32*i+j]=int(lineStr[j])
return returnVect
def loadImages(dirName):
from os import listdir
hwLabels=[]
print(dirName)
trainingFileList=listdir(dirName)#load the training set
m=len(trainingFileList)
trainingMat=zeros((m,1024))
for i in range(m):
fileNameStr=trainingFileList[i]
fileStr=fileNameStr.split('.')[0]
classNumber=int(fileStr.split('_')[0])
if classNumber==9:
hwLabels.append(-1)
else:
hwLabels.append(1)
trainingMat[i, :] = img2vector('%s/%s' % (dirName, fileNameStr))
return trainingMat, hwLabels
def testDigits(kTup=('rbf',10)):
#1.导入训练数据
dataArr,labelArr=loadImages('6.SVM/trainingDigits')
b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
datMat=mat(dataArr)
labelMat=mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd]
labelSV=labelMat[svInd]
# print("there are %d Support Vectors"% shape(sVs)[0])
m,n=shape(datMat)
errorCount=0
for i in range(m):
kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
# 1*m * m*1 = 1*1 单个预测结果
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the training error rate is: %f" % (float(errorCount) / m))
# 2. 导入测试数据
dataArr, labelArr = loadImages('6.SVM/testDigits')
errorCount = 0
datMat = mat(dataArr)
labelMat = mat(labelArr).transpose()
m, n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs, datMat[i, :], kTup)
predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
if sign(predict) != sign(labelArr[i]): errorCount += 1
print("the test error rate is: %f" % (float(errorCount) / m))
ws=calcWs(alphas,dataArr,labelArr)
plotfig_SVM(dataArr,labelArr,ws,b,alphas)
def plotfig_SVM(xArr,yArr,ws,b,alphas):
'''
参考地址:
http://blog.csdn.net/maoersong/article/details/24315633
http://www.cnblogs.com/JustForCS/p/5283489.html
http://blog.csdn.net/kkxgx/article/details/6951959
'''
xMat=mat(xArr)
yMat=mat(yArr)
# b 原来是矩阵,先转为数组类型后其数组大小为(1,1),所以后面加【0】,变为(1,)
b=array(b)[0]
fig=plt.figure()
ax=fig.add_subplot(111)
#注意flatten的用法
ax.scatter(xMat[:,0].flatten().A[0],xMat[:,1].flatten().A[0])
#x最大值,最小值根据原数据集dataArr[:0]的大小而定
x=arange(-1.0,10.0,0.1)
#根据x.w+b=0 得到,其式子展开为w0.x1+w1.x2+b=0,x2就是y值
y=(-b-ws[0,0]*x)/ws[1,0]
ax.plot(x,y)
for i in range(shape(yMat[0, :])[1]):
if yMat[0, i] > 0:
ax.plot(xMat[i, 0], xMat[i, 1], 'cx')
else:
ax.plot(xMat[i, 0], xMat[i, 1], 'kp')
# 找到支持向量,并在图中标红
for i in range(100):
if alphas[i] > 0.0:
ax.plot(xMat[i, 0], xMat[i, 1], 'ro')
plt.show()#无核函数测试
#获取特征和目标变量
dataArr,labelArr=loadDataSet('6.SVM/testSet.txt')
#print labelArr
#b是常量值,alphas是拉格朗日乘子
b,alphas=smoP(dataArr,labelArr,0.6,0.001,40)
print('/n/n/n')
print('b=',b)
print('alphas[alphas>0]=',alphas[alphas>0])
print('shape(alphas[alphas>0])=',shape(alphas[alphas>0]))
for i in range(100):
if alphas[i]>0:
print(dataArr[i],labelArr[i])
#画图
ws=calcWs(alphas,dataArr,labelArr)
plotfig_SVM(dataArr,labelArr,ws,b,alphas)
#有核函数测试
testRbf(0.8)
#项目实战
#手写数字识别
testDigits(('rbf', 0.2))以上为jupyter实现