题目描述

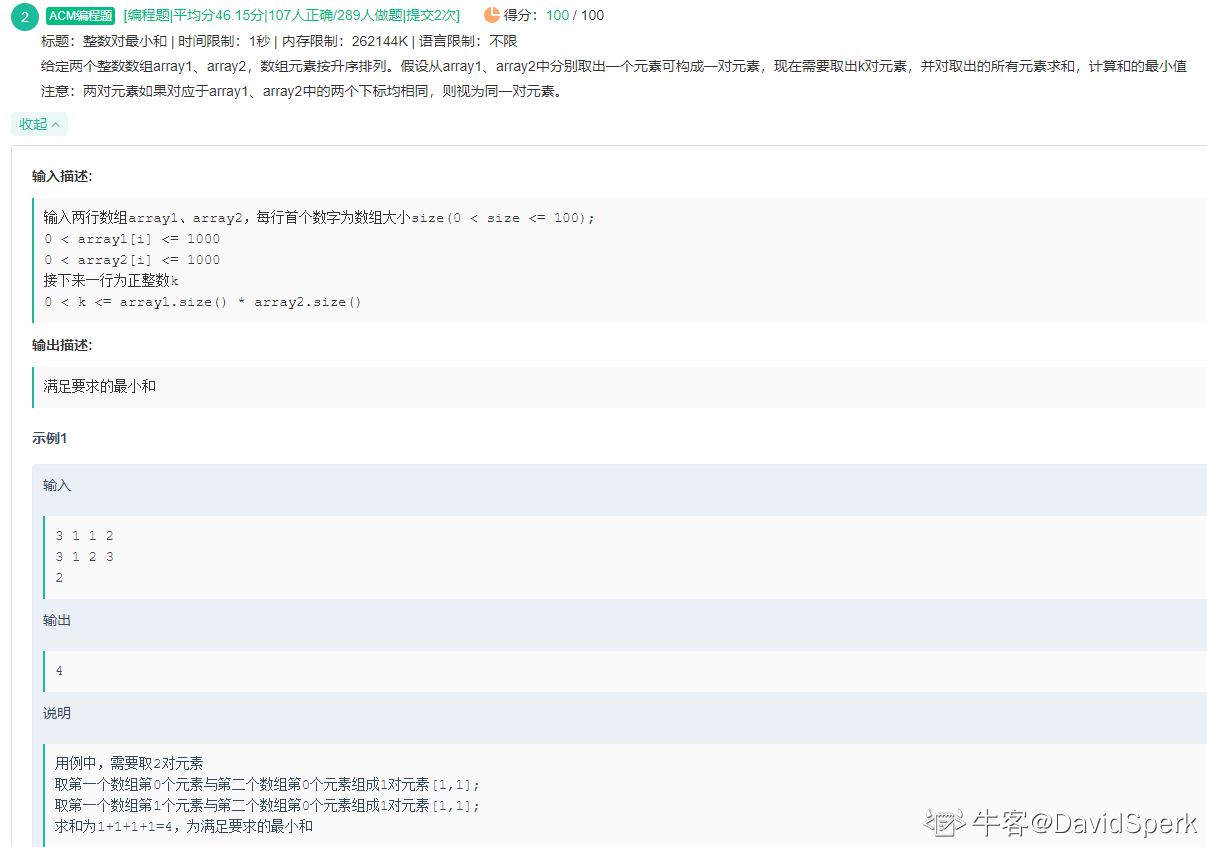
给定两个整数数组array1、array2，数组元素按升序排列。假设从array1、array2中分别取出一个元素可构成一对元素，现在需要取出k对元素，并对取出的所有元素求和，计算和的最小值

 

代码实现

# coding:utf-8
class Solution:
    def minArraySum(self, k, arr1,arr2):
        sum = 0
        res = []
        for i in arr1:
            for j in arr2:
                res.append(i + i)
        res.sort()
        for i in range(k):
            sum += res[i]
        return sum