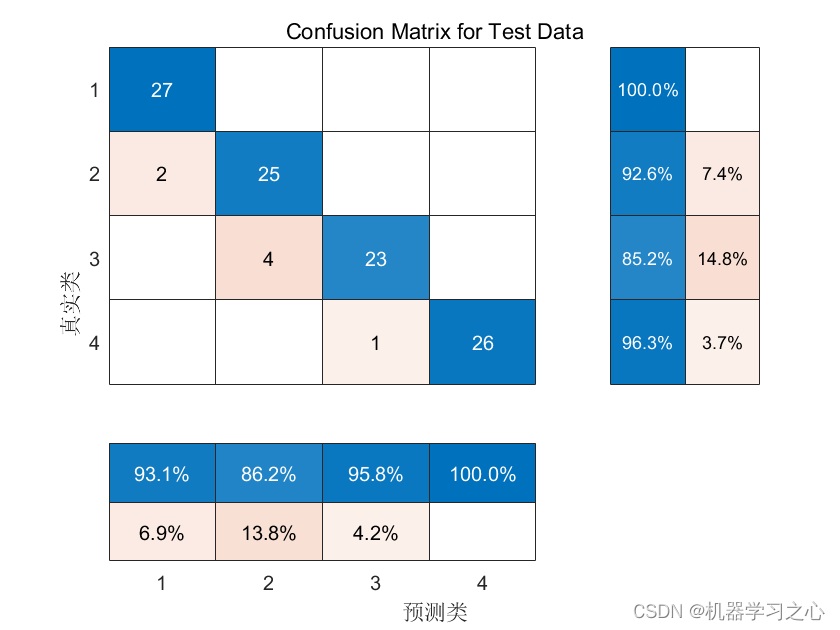
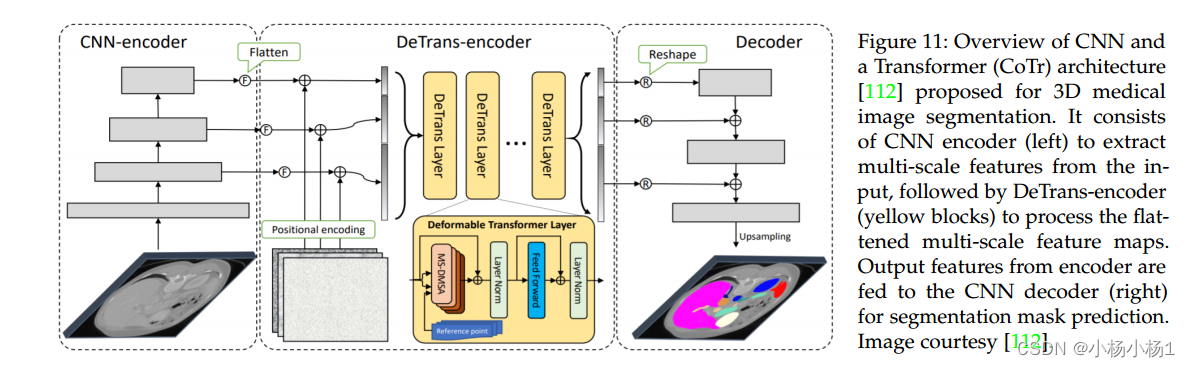
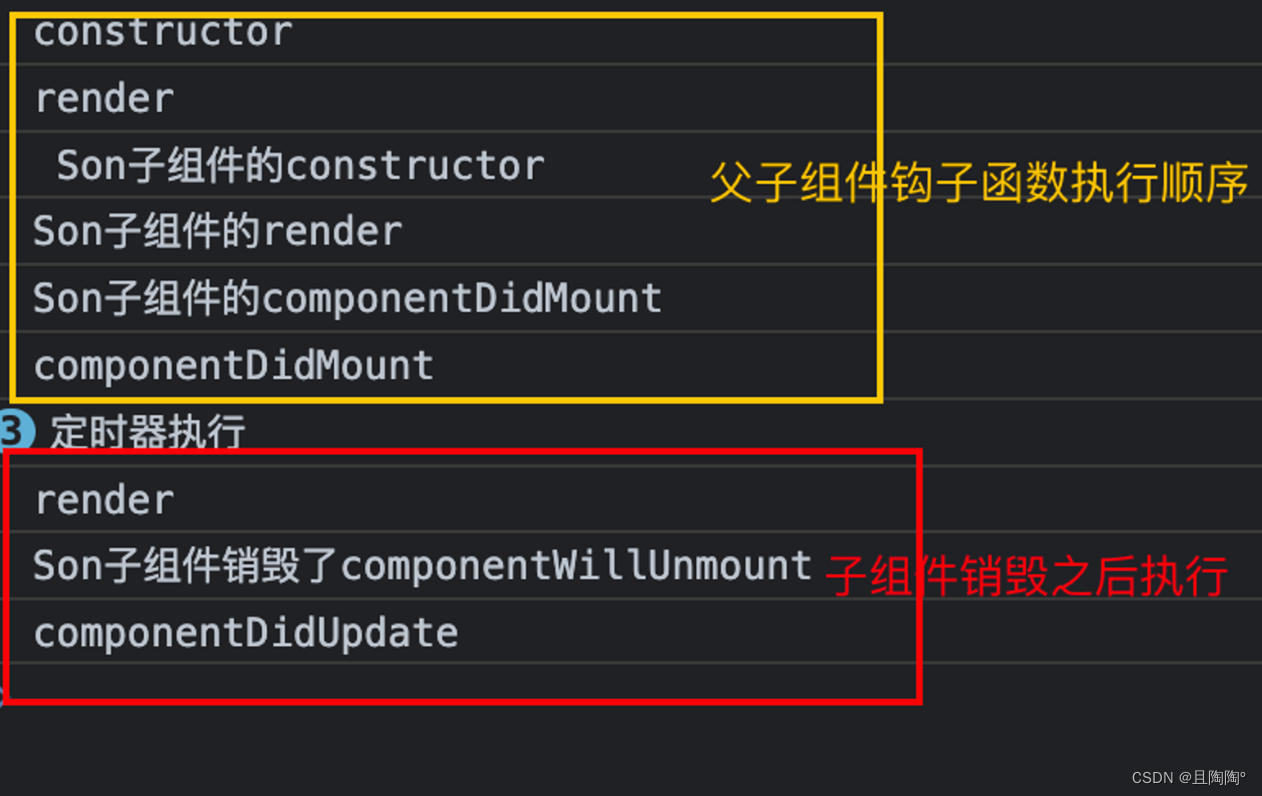
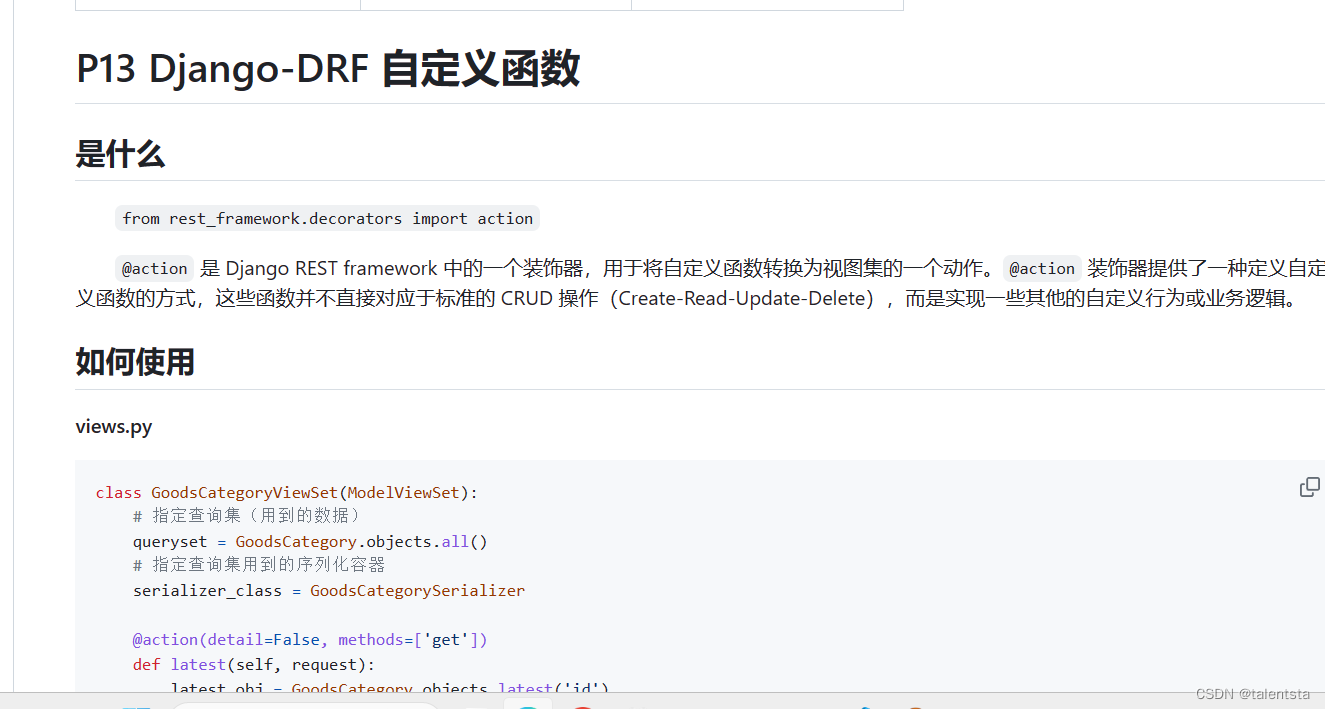
目录
题目要求:
题目内容:
思路展开:
代码演示:
题目要求:
一个数组中只有两个数字是出现一次,其他所有数字都出现了两次编写一个函数找出这两个只出现一次的数字。
题目内容:
有数组的元素是: 1,2,3,4,5,1,2,3,4,6 只有5和6只出现1次,要找出5和6。
思路展开:
- 首先,我们先去除一个数字,只留下 1,2,3,4,5,1,2,3,4 这时候,我们想要取出只出现一次的数字,我们可以采用全员^的方式,进行提取,这里利用了^的原理,1^1=0 1^0=0
- 所以,这一题无异于是变成了两个,如果变成了两个只出现一次的数字,我们可以将其分为两个部分。
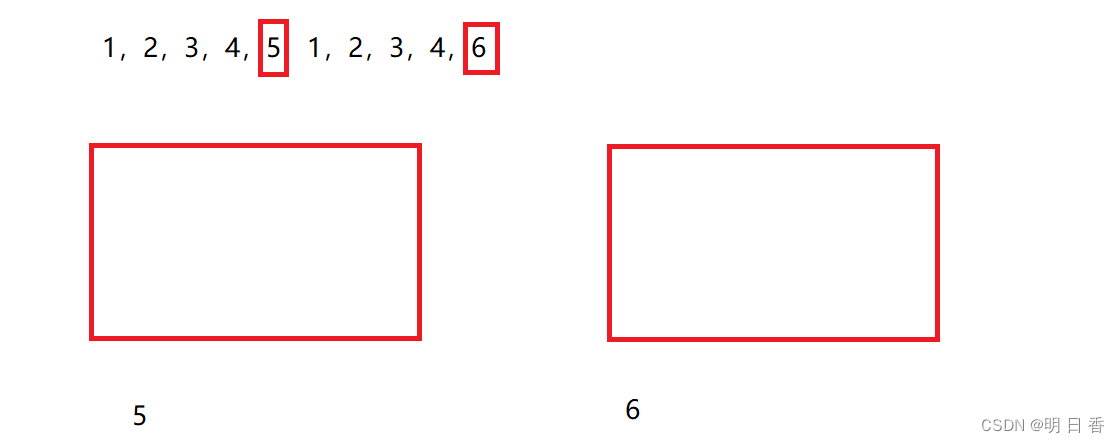
- 这里使用了^操作符,那我们就要注意,这题大概需要使用的就是二进制数位来进行操作。
- 而若使用二进制数位进行操作,那么我们是否可以使用二进制数位的不同以此来将整个数组进行分离,分离成两个部分。

- 通过发现,得知,我们可以通过二进制数位的某一位不同来进行判断和分离,而二进制数是由0和1组成的,所以可以看某一位是0是1来进行分离。
- 那么就可以通过先>> 或是<< 在使用&1来进行判断某一位数位是否是1。
- 且,在通过二进制数位不同的地方来分离之前,我们要先判断不同的地方在何处,或是说在那个位置,所以我们第一时间使用^将二者的不同之处展示出来,以便于接下来的分离。
- ^是同位置数位,不同的数最后的结果是1,相同的数是0,所以先进行5^6的操作,来表明不同之处,而下一步的目的,也就从寻找不同之处,变为了寻找那一个位置是1。
- 而5^6在题目中,相当于整个数组进行全员^。
int ret = 0;
for (int i = 0;i < len; i++)
{
ret ^ = arr[i];
}
而下一步,为了寻找哪一位是1,1的位置在哪里。
int pos = -1;
for (int i = 0; i < 32; i++)
{
if (ret & (1<< i)) //先将1进行移位,在结合&的特性来判断每一位是否是1
{
pos = i;
break;
}
}
& - 是同为1才为1,不同为0
- 这一步是为了记录不同之处的位置,也就是1所处在的位置,以便接下来的分离操作。
- 使用了 & 1的特性来判断这个数字是否是1 ,又使用了<<的功能,来进行判断二进制数位的每一位数位。
具体详细:http://t.csdn.cn/leuTQ
for (int i = 0; i < len; i++)
{
if ((arr[i] >> pos) & 1)
{
*pnuml ^ = arr[i];
}
else
{
*pnum2 ^ = arr[i];
}
}
- 当数字的二进制数位 在pos 这个位置为1时((arr[i]>>pos)——利用了&的特性,二进制数位同为1时才会为1 ),开始进行分离运算。
- 而运算的过程,就是分为两个部分后,两个部分各个进行全员^。
代码演示:
void func(int* arr, int len, int* pnum1, int* pum2)
{
int ret = 0;
for (int i = 0; i < len; i++)
{
ret ^= arr[i];
}
int pos = -1;
for (int i = 0; i < 32; i++)
{
if ((ret & 1) << i)
{
pos = i;
break;
}
}
for (int i = 0; i < len; i++)
{
if ((arr[i] >> pos) & 1)
{
*pnum1 ^= arr[i];
}
else
{
*pum2 ^= arr[i];
}
}
}
int main()
{
int ret1 = 0, ret2 = 0;
int arr[] = { 1,2,3,4,5,1,2,3,4,6 };
int len = sizeof(arr) / sizeof(arr[0]);
func(arr,len,&ret1,&ret2);
printf("%d %d",ret1,ret2);
return 0;
}