MemSeg:一种差异和共性来检测图像表面缺陷的半监督方法

1、摘要

2、Method

2.1 模拟异常样本

2.2 Memory Module

2.3 空间注意模块

2.4 多尺度特征融合模块

2.5 损失函数设置

2.6 Decoder模块

1、摘要

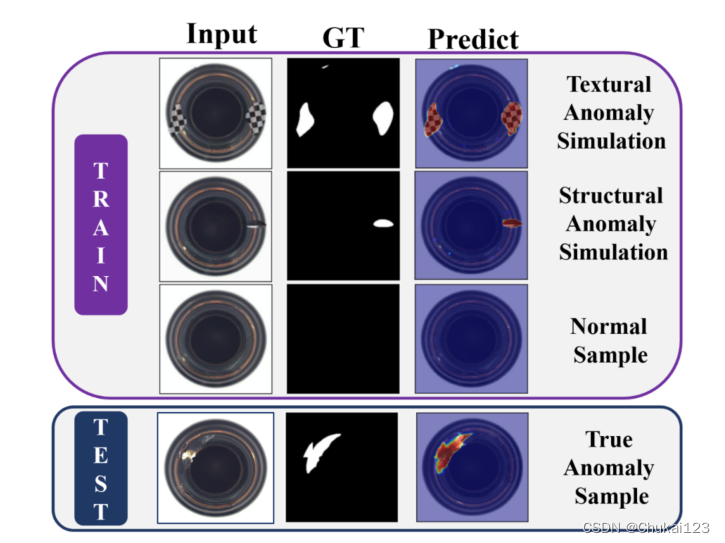
本文认为人为创建类内差异和保持类内共性可以帮助模型实现更好的缺陷检测能力，从而更好地区分非正常图像。如图一所示。

差异（differences）:

MemSeg引入人工模拟的异常图像在训练阶段使模型能够区分正常和异常的图像，减轻了半监督学习只能用正常样本进行训练的不足，然后在推理阶段可以直接输入图像无需做任何后处理。

共性（commonalities）:

MemSeg引入了一个记忆池来记录正常样本的通用模式，在训练和推理阶段，比较输入图像和记忆池中的样本之间的差异，为异常区域的定位提供有用的信息。同时为了更好地协调来自记忆池和输入图像的信息，还引入了多尺度特征融合模块和空间注意模块。

论文主要贡献：

设计了一种异常模拟策略来进行模型的自监督学习，该方法整合了目标前景异常、纹理异常和结构异常。
提出了一种具有更有效的特征匹配算法的记忆模块，并在U-net结构中引入正常模式的记忆信息来辅助模型学习。
结合上述两点，并结合多尺度特征融合模块和空间注意模块，将半监督异常检测简化为端到端语义分割任务，使半监督图像表面缺陷检测更加灵活。
通过实验验证，MemSeg在表面缺陷检测和定位任务中具有较高的精度，同时可以更好地满足工业场景的实时需求。

2、Method

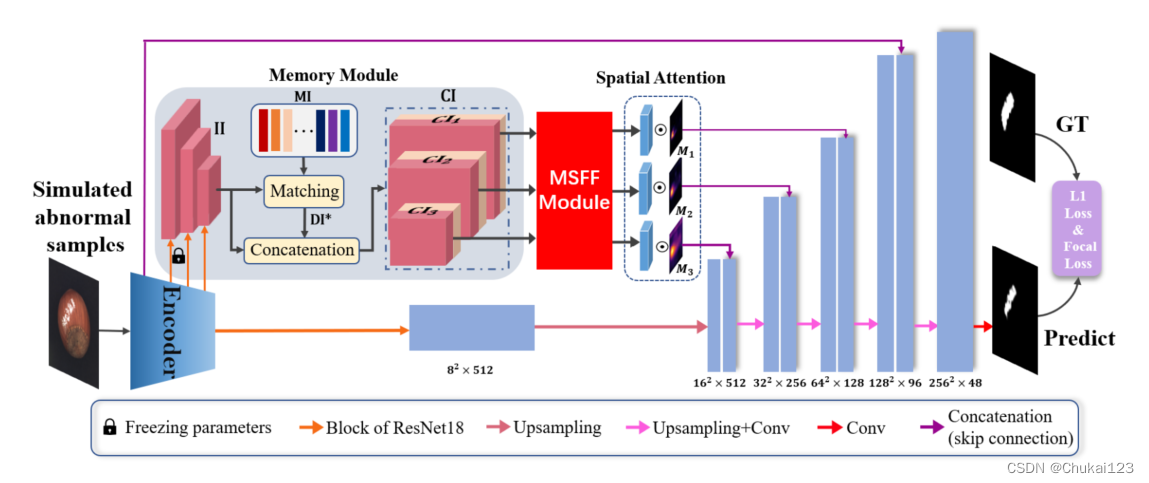
MemSeg采用U-Net作为框架，在训练阶段利用模拟的异常图片和记忆信息来完成语义分割任务，如上图所示采用预训练的ResNet18作为编码器，从左到右依次为：模拟异常样本->记忆模块->多尺度特征融合模块->空间注意模块->采用双损失函数进行端到端训练。

2.1 模拟异常样本

实际场景下数据集不可能覆盖所有的异常，同时在半监督框架中仅使用正常样本进行训练而不与异常样本进行比较不足以让模型了解什么是正常模式，本文提出的方法主要有三个步骤：

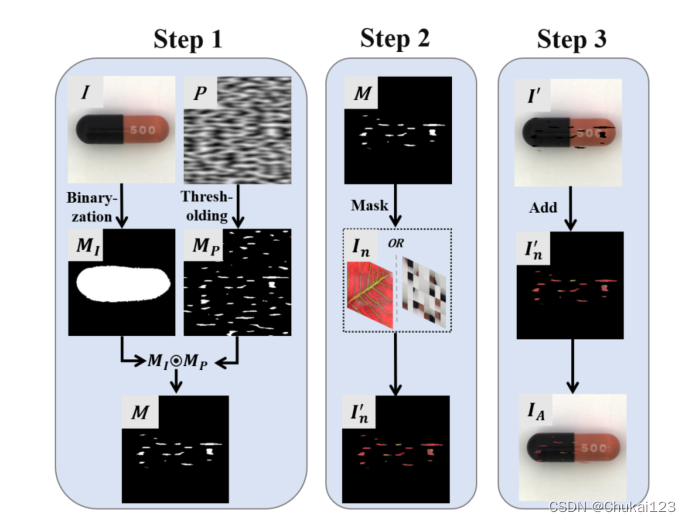
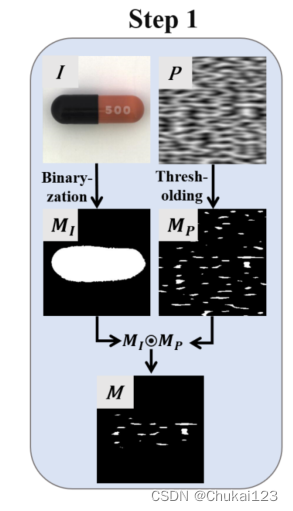
step1:

生成一个二维的Perlin噪声P，然后通过阈值T进行二值化得到掩码Mp，perlin噪声中有多个随机峰值，由它得到的Mp可以提取图像中连续的区域块，同时考虑到采集图像中某些工业成分主体的比例比较小，如果不进行处理直接进行数据增强，容易在图像的背景部分产生噪声，增加模拟异常样本与真实样本在数据分布上的差异，不利于模型学习有效的鉴别信息，因此对这类图像采用前景增强策略，使用开操作和闭操作去除在二值化处理中产生的噪声，即输入图像对应的Mi，然后通过对获得的两个掩码进行元素级乘积得到最终的掩码图像M。

注意：

(1)Perlin噪声是一种用于计算机图形学中的随机噪声函数，它是一种连续可微的梯度噪声函数，由Ken Perlin于1983年发明。Perlin噪声可以用于生成自然界中的各种纹理，例如云彩、火焰、树木等。它在游戏开发中也得到了广泛应用。

Perlin噪声的原理是将坐标系划分成一块一块的晶格，之后在晶格的顶点处生成一个随机的梯度，通过与晶格顶点到晶格内点的向量进行点乘加权计算后得到噪声。

(2)在图像处理中，开操作和闭操作是形态学图像处理中的两种基本操作。开操作可以平滑物体轮廓、断开较窄的狭颈并消除细的突出物，而闭操作则可以弥合较窄的间断和细长的沟壑，消除小的孔洞，填补轮廓线中的断裂。

在Python中，我们可以使用OpenCV库来实现形态学图像处理中的开操作和闭操作。下面是一个示例代码，演示如何使用OpenCV实现这两种操作：
import cv2
import numpy as np

# 读取图像
img = cv2.imread('image.jpg', 0)

# 定义结构元素
kernel = np.ones((5,5),np.uint8)

# 进行开操作
opening = cv2.morphologyEx(img, cv2.MORPH_OPEN, kernel)

# 进行闭操作
closing = cv2.morphologyEx(opening, cv2.MORPH_CLOSE, kernel)

# 显示结果
cv2.imshow('Original Image', img)
cv2.imshow('Opening', opening)
cv2.imshow('Closing', closing)
cv2.waitKey(0)
cv2.destroyAllWindows()
在这个示例中，我们首先读取了一张灰度图像，然后定义了一个5x5的结构元素。接下来，我们使用`cv2.morphologyEx()`函数分别对原始图像进行了开操作和闭操作，并将结果显示出来。

需要注意的是，在进行形态学操作之前，我们需要将图像转换为灰度图像，并确保图像的大小和结构元素的大小相同。此外，我们还可以使用不同的结构元素来获得不同程度的平滑效果。

元素级别乘积：

指对两个数组中每个位置上的元素进行乘法运算。这意味着两个数组必须具有相同的形状，否则就会出现形状不匹配的错误。例如，我们可以通过以下代码创建两个2×2的NumPy数组：

import numpy as np

a = np.array([[1, 2], [3, 4]])

b = np.array([[5, 6], [7, 8]])

现在，我们将使用元素级别乘法将这两个数组相乘：

c = np.multiply(a, b)

print(c)

这将输出： array([[ 5, 12], [21, 32]])

我们可以看到，在每个位置上，一个数组中的元素与另一个数组中的相应元素进行了乘法运算，并将结果存储在输出数组中。

step2:

第一步得到的掩码图像M和噪声图像In执行元素级乘积得到由M定义的In中的感兴趣区域。与DREAM方法保持一致，在这个过程中引入了一个透明度因子来平衡原始图像和有噪声图像的融合，从而模拟异常模式更接近真实异常。

$I_{n}^{'}=\sigma (M\odot I_{n} )+(1-\sigma )(M\odot I)$

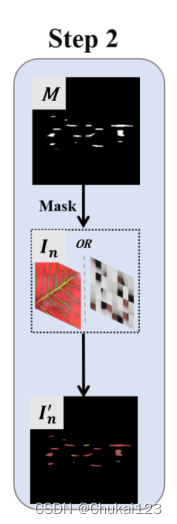
其中sigma代表透明度因子，采用上述公式可以得到有噪声的前景图像，对于噪声图像 $I_{n}$ ，希望其最大透明度，以增加模型学习的能力，其中sigma的取值范围为[0.15，1]。

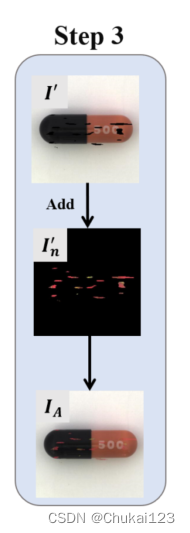
step3:

掩码图像M转换成 $\bar{M}$ ，然后在 $\bar{M}$ 和原始图像I上执行元素级乘积，得到图像 $I^{'}$ ，根据下述公式：

$I_{A}=\bar{M}\odot I+I_{n}^{'}$

得到数据增强图像 $I_{A}$ ，即模拟异常图像，它采用原始输入图像I作为背景，以掩码图像M提取的噪声图像 $I_{n}$ 中的ROI作为前景。

2.2 Memory Module

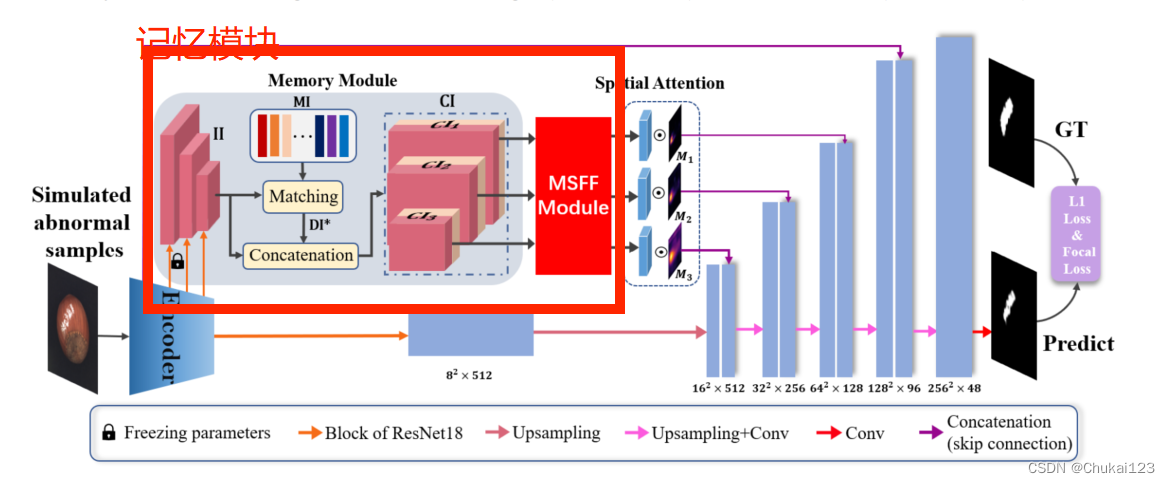
人类的异常区域是通过比较测试图像和记忆中的正常图像来获得的，本文采用少量正常的样本作为记忆样本，并使用预训练ResNet18提取记忆样本的高级特征作为记忆信息，以协助MemSeg学习。

具体方法：从训练集中随机选择N张正常图像作为记忆样本，然后通过ResNet18得到三个不同维度的特征：N×64×64×64、N×128×32×32和N×256×16×16（分别表示block1、block2、block3），然后将三个block一起组成记忆信息MI，为了确保记忆信息和输入图像的高级特征的统一，于是冻结ResNet18在block1、block2、block3中的模型参数，但是模型其他部分是可训练的。

然后计算所有记忆样本与输入图像之间的L2距离，从而得到输入图像与记忆样本之间的N差分信息DI。

$DI=\bigcup_{i=1}^{N}\left \| MI_{i} - II \right \|_{2}$

L2距离是指两点之间的欧几里得距离，也称为直线距离。该距离是在n维空间中两个点之间的最短距离，其中n可以是任何正整数。

L2距离的计算方式是两个向量中每个元素相减后平方，再求和，最后取平方根。例如，对于两个n维向量X=(x1,x2,...,xn)和Y=(y1,y2,...,yn)，L2距离的计算公式为： $D(X,Y)=\sqrt{\sum_{i=1}^n{(x_i-y_i)^2}}$ 其中 $\sum_{i=1}^n{(x_i-y_i)^2}$ 是X和Y中每个元素差的平方和。

其中N是记忆样本数，对于N个差分信息，以每个DI中所有元素的最小和为标准，得到II和MI之间的最佳差分信息，也就是

$DI^{*}=argmin_{DI_{i}\epsilon DI}\sum_{x\epsilon DI_{i}}x$

其中i取值范围[1,N]，最佳差分信息 $DI^{*}$ 包含输入样本与其最相似的记忆样本之间的差，一个位置的差值越大，输入图像与该位置对于的区域异常的概率就越高。

和标准进行比较，与标准差别越大就表示其很大概率是异常图像！

为什么采用ResNet18的高级特征？（其他网络应该也可以吧TODO）

因为预训练模型在大量数据上进行了训练，学习到了通用的特征表示，这些特征可以很好地推广到新的任务上。通过迁移学习，我们可以利用预训练模型学到的特征表示，来加速我们自己的模型训练过程，同时提高模型的性能。

高级特征？

是指从深度学习模型中提取出来的更加抽象、更加具有语义信息的特征，这些特征往往是在深层网络中提取出来的。与低级特征相比，高级特征更加抽象，更加难以描述，但是它们能够更好地表达数据之间的复杂关系，从而提高模型的性能。

随后，将获得的最佳差分信息 $DI^{*}$ 和输入图像II提取的高级特征执行串联操作，得到对应的串联信息 $CI_{1}$ ， $CI_{2}$ ， $CI_{3}$ 。最后拼接后的信息通过多尺度特征融合模块进行特征融合，融合后的特征通过U-Net的跳连接传到解码器。

2.3 空间注意模块

为了充分利用差分信息，利用 $DI^{*}$ 提取了三张空间注意图，用于加强对异常区域的最佳差分信息的猜测，对于 $DI^{*}$ 中三个不同维度的特征，在通道维度计算平均值，分别得到大小为16×16、32×32和64×64的三个特征图。

16×16特征图直接用作空间注意图：M3，使用32×32特征图和上采样后的M3进行元素级乘积操作获得M2；再使用64×64特征图和上采样后的M2执行元素级乘积操作获得M1。

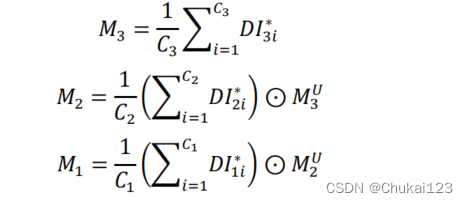
如上图所示，空间注意图M1，M2，M3分别和经过多尺度特征融合处理后获得的信息进行加权，求解过程如上述公式所示。其中C3表示 $DI_{3}^{*}$ 的通道数量， $DI_{3i}^{*}$ 表示通道i的特征图像， $M_{2}^{U}$ 表示上采样后的特征图。

特征图上采样？

是指将特征图的大小扩大，通常是通过复制边缘像素或者插值的方式来实现。上采样可以增加模型的感受野，从而提高模型的性能。常见的上采样方法有最近邻插值、双线性插值、双三次插值等。

通道维度？

指图像中的颜色通道，例如RGB图像有三个颜色通道。在卷积神经网络中，通道维度通常用于表示输入图像的通道数。例如，对于32×32×3大小的输入图像，其通道数为3。

2.4 多尺度特征融合模块

通过记忆模块，得到输入图像信息II和最佳的差分信息 $DI^{*}$ 组成的串联信息CI，直接使用这个串联信息存在特征冗余的问题，同时会降低推理速度。利用通道注意力机制和多尺度特征融合策略充分融合视觉信息和语义信息。

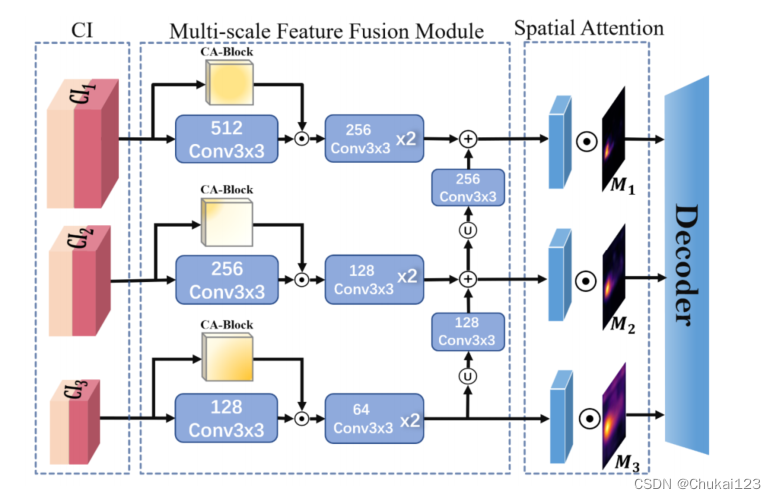
对于串联信息 $CI_{n}(n=1,2,3)$ ，最开始经过一个3×3的卷积操作？

不采用2×2卷积，如果使用偶数大小的卷积核，网络在进行卷积操作时很难找到卷积的中心点，也就是偶数卷积核不对称这个问题也导致了导致在填充的（padding）的时候像素特征不断偏移。然后随着层次的加深，这个偏移现象就越来越明显。这种偏移问题，在一些任务，比如语义分割，等一些需要知道特征具体像素位置的任务中就产生了很大的影响。

相比之下，3×3卷积可以保留更多的空间信息，因为它可以通过重叠存储来捕获更大的区域。这使得3×3卷积在图像处理中更加灵活和可靠。

同时考虑到 $CI_{n}(n=1,2,3)$ 是通道维度中两种信息的简单连接，使用坐标注意（CA）来捕获 $CI_{n}(n=1,2,3)$ 信道之间的信息关系。

然后，对于不同维度的特征加权坐标注意力，继续执行多尺度信息融合：不同维度的特征图首先采用上采样法进行分辨率对齐，然后利用卷积对通道数进行对齐，最后执行元素级加法操作，实现多尺度特征融合。融合后的特征与空间注意图 $M_{n}(n=1,2,3)$ 进行加权。然后输入给最终的解码器。

2.5 损失函数设置

采用L1损失和focal损失来保证图像空间中所有像素的相似性。focal损失减轻了图像中正常区域和异常区域之间的面积不平衡问题，使模型更加关注困难样本的分割，以提高异常分割的精度

L1损失相对L2损失来说能够保持更多的边缘信息。

L1损失函数和L2损失函数？

都是机器学习中的常用损失函数，它们的区别在于对于异常值的敏感程度不同。L1损失函数对异常值更加鲁棒，因为它会把权重向量中小于某个阈值的元素都变为0，而L2损失函数则对异常值很敏感。但是，L1损失函数的导数是不连续的，从而让它无法有效地求解；而L2损失函数的导数是连续的，因此可以有效地求解。

Focal Loss损失函数？

是何恺明大神在RetinaNet网络中提出的，主要目的是为了解决one-stage目标检测中正负样本极不平衡的问题。它是基于二分类交叉熵CE的，是一个动态缩放的交叉熵损失，通过一个动态缩放因子，可以动态降低训练过程中易区分样本的权重，使得模型更加关注难以分类的样本。

Focal Loss的计算公式如下： $FL(p_t)=-(1-p_t)^\gamma \log(p_t)$ 其中， $p_t=\left\{\begin{array}{l}p, if y=1\\ 1-p, otherwise\end{array}\right.\gamma$ 为常数，当其为0时，FL就和交叉熵损失函数一样。当 $gamma>0$ 时， $FL$ 会使得难分类样本的损失变小，而易分类样本的损失不变。

2.6 Decoder模块

对于解码器部分，如图2所示，上采样层包含一个双线性插值层和一个基本的由卷积层、批归一化和一个ReLU激活函数组成的卷积块。Conv层包含两个堆叠的基本卷积块；只有最后一个Conv层包含一个基本卷积块和一个2通道卷积层。

双线性插值是一种用于重新采样图像和纹理的算法，它通过在两个方向上进行一次线性插值，然后在另一个方向上进行一次线性插值，得到一个加权平均值。

MemSeg的训练过程经过2700次迭代，输入图像的大小设置为256×256，批量大小设置为8，其中包含4个正常样本和4个模拟异常样本。在进行异常模拟时，大多数类别使用纹理异常模拟和结构异常模拟的概率相等。

使用网格搜索来设置超参数：使用的学习率设置为0.04；focal损失中的Gamma设置为4；目标函数中的 $\lambda _{l1}$ 和 $\lambda _{f}$ 分别设置为0.6和0.4。

网格搜索（Grid Search）是一种穷举搜索方法，它通过遍历超参数的所有可能组合来寻找最优超参数。网格搜索首先为每个超参数设定一组候选值，然后生成这些候选值的笛卡尔积，形成超参数的组合网格。对于每一种组合，都会训练模型并计算验证集上的误差。最后，选择误差最小的超参数组合作为最终的超参数组合。

以下是一个使用网格搜索的例子，用于调整支持向量机（SVM）的超参数：

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC

# 定义超参数组合
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': [1, 0.1, 0.01, 0.001],
    'kernel': ['rbf', 'poly', 'sigmoid'],
}

# 创建SVM分类器对象
svm = SVC()

# 创建网格搜索对象，传入超参数组合和分类器对象
grid_search = GridSearchCV(svm, param_grid=param_grid)

# 训练模型并输出最佳超参数组合和对应的准确率
grid_search.fit(X_train, y_train)
print("Best parameters:", grid_search.best_params_)
print("Best accuracy:", grid_search.best_score_)