论文解读：李欣 马玺渊

作者：Gah-Yi Ban, Cynthia Rudin

引用：Ban, Gah-Yi and Cynthia Rudin. The big data newsvendor: Practical insights from machine learning. Operations Research 67.1 (2019): 90-108.

文章链接：https://doi.org/10.1287/opre.2018.1757

问题与方法简述

文章研究了大规模数据驱动的报童问题（包括$p$个关于需求的特征和$n$个观测值），并围绕以下四个问题展开讨论：

问题一：决策者应如何使用特征需求数据集来解决报童问题？

问题二：在报童模型决策中纳入特性的价值是什么？

问题三：使用这些数据的决策者有什么理论保证最优性？以及这些保证如何与各种问题的不同参数进行变化？

问题四：在实践中，基于特征需求数据集的报童决策与其他基准方法相比如何？

此处的“特征”指的是指外生变量（也称为协变量、属性和解释变量），它们是需求的预测因子，在需求发生之前可供决策者使用。

问题一：决策者应如何使用特征需求数据集来解决报童问题？

文章提出了两类一步式方法，基于给定的需求与相关特征数据的观测值，确定基于最优订货数量。

• 其一基于经验风险最小化方法 (Empirical Risk Minimization, ERM) （详见 Vapnik, 1998）, 适用于实施或不实施正则化两种情况。文章表示，ERM相当于高维分位回归（一种用于估计因变量和自变量关系的方法，特别适用于高维度的数据集）：当不涉及正则化时，ERM方法可以看作是一种线性规划算法。当涉及正则化时，根据所使用的正则化类型（${\ell }_0,{\ell }_1,{\ell }_2$正则化），ERM方法可以被转化为混合整数规划、线性规划，或二阶锥规划 (Second Order Cone Programming, SOCP).
• 其二为核权重优化 (Kernel-weights Optimization, KO)，可参见 Nadaraya-Watson 核回归方法 (Nadaraya-Watson kernel regression method: Nadaraya, 1964; Watson, 1964) . 该方法下的最优数据驱动订货量可由简单的排序算法求得。

问题二：在报童模型决策中纳入特性的价值是什么？

文章通过回答问题二来证明使用特征的合理性，其中通过与没有任何特征的决策进行比较（样本平均近似，Sample Average Approximation, SAA）来分析量化特征的价值。 文章考虑两种需求模型（双人口模型和线性需求模型）的比较，并表明：无特征 SAA 决策不会收敛到真正的最优决策，而基于特征的 ERM 决策则会收敛；换句话说，无论决策者有多少个观测值，SAA 决策都有恒定偏差（即 $O(1)$误差），而当$n$趋于无穷大时，基于特征的决策的任何有限样本偏差都会缩小到零 。 因此，SAA 决策可能比 ERM 决策具有更高的报童成本。

问题三：使用这些数据的决策者有什么最优性保证？以及这些保证如何与各种问题的不同参数进行变化？

在实践中，由于数据有限，决策者可能永远无法做出真正最优的决策。为了解没有完整需求分布信息的情况下的权衡，文章推导了所提出算法的理论性能界限，其包括样本内决策成本（与样本内决策的期望成本相对）与问题的各种参数，特别是$p$和$n$的真实预期成本之间的偏差。这些界限显示了样本内决策的样本外成本（“泛化误差”）如何通过一个复杂度项来偏离其样本内成本。从实际角度来看，这些界限明确表现了泛化误差（衡量样本内过拟合程度）和有限样本偏差之间的权衡，以及它们如何依赖于数据集的大小、报童成本参数和算法中的任何自由参数（控制变量）。

问题四：在实践中，基于特征需求数据集的报童决策与其他基准方法相比如何？

文章通过建立于医院急诊室的护士排班问题进行了实证研究且评估了所提出的两类算法。

• 对于ERM算法，最优结果通过进行 ${\ell }_1$正则化获得，其相对于最佳实践基准（按周中的某天聚类的样本平均近似值），成本降低了 23%.
• 相对于相同的基准，使用 KO 方法的最佳结果是成本降低了 24%。两项结果均在 5% 水平上具有统计显著性。
• 计算效率方面，通过排序过程求解的最佳 KO 方法效率极高，其只需 0.05 秒即可计算出下一个时期的最佳人员配置水平，这比最佳 ERM 方法快三个数量级，比最佳实践基准和其他基准快两个数量级。

基于特征的报童模型 （问题一）

传统的报童问题是一家公司销售易腐商品，在观察到不确定的需求之前需要下订单，目标是确定订购数量，使总预期成本最小化，即

其中$q$是订购量，$D\in \mathbb{D}$是不确定（随机）的未来需求，

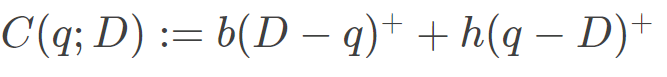
为订单 $q$和需求 $D$的随机成本，$b$和 $h$分别是单位缺货成本和单位持有成本。若需求分布 $F$ 是已知的，则可以示出由$b/(b+h)$分位数给出最优决策，即：

数据驱动报童模型考虑到实际中去决策者并不清楚真实需求分布的情况。若仅可以访问历史需求观测$\mathbf{d}(n)=[d_1,d_2,\dots ,d_n]$，则可用样本平均期望值代替真实期望值，即

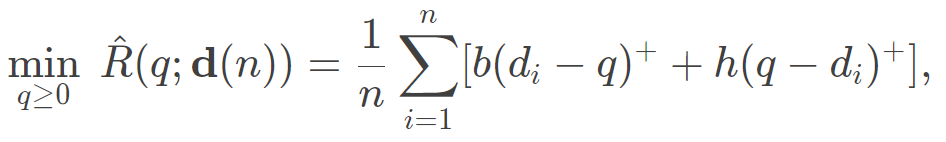
其中 $\hat{\cdot }$表示根据数据估计的订购量，其最优SAA决策为

q ∗ = inf ⁡ { y : F n ^ ( y ) ≥ b b + h } , q^{*}= \inf{\{y:\hat{F_n}(y)\geq }\frac{b}{b+h}\}, q∗=inf{y:Fn​^​(y)≥b+hb​},

其中$\widehat{F_n}(.)$是来自$n$个观测需求的经验累积分布函数。

基于特征的报童模型 在实践中，需求取决于许多可观察到的特征，例如季节性、天气、位置和经济指标，其皆可在下订单前已知并用于订单决策中。于是，实际报童问题为最优条件期望成本函数（此处定义为问题1）：

其中$\mathbf{x}$是高维特征，需求$D(\mathbf{x})$是特征向量$\mathbf{x}$的函数。此时的决策则为一个将特征空间$\mathcal{X}\subset {\mathbb{R}}^p$映射到实数空间的函数，而要最小化的期望成本则以特征向量$\mathbf{x}\in \mathcal{X}\subset {\mathbb{R}}^p$为条件。

基于特征的报童模型的求解算法（问题一）

ERM 算法

假设决策者已经收集了适当的历史数据$S_n=[({\mathbf{x}}_1,d_1),\dots ,({\mathbf{x}}_n,d_n))]$，每个特征$\mathbf{x}$均是 $p$维的。解决基于特征的报童模型的ERM算法可描述为 (NV-ERM)
min ⁡ q ( . ) ∈ Q , { q : X → R } R ^ ( q ( . ) ; S n ) = 1 n ∑ i = 1 n [ b ( d i − q ( x i ) + + h ( q ( x i ) − d i ) + ] , \displaystyle\min_{q(.)\in\mathcal{Q},\{q:\mathbf{X}\rightarrow \mathbb{R\}}}\hspace{0.15cm} \hat{R}(q(.);S_n)=\frac{1}{n} \sum_{i=1}^n[b(d_i-q(\mathbf{x}_i)^{+}+h(q(\mathbf{x}_i)-d_i)^+], q(.)∈Q,{q:X→R}min​R^(q(.);Sn​)=n1​i=1∑n​[b(di​−q(xi​)++h(q(xi​)−di​)+],

其中$\hat{R}$为函数$q$相对于数据集$S_n$的经验风险。假设$q$可由某些参数表示，文章考虑以下线性决策形式：
Q = { q : X → R : q ( x ) = q ′ x = ∑ j = 1 p q j x j } . \mathcal{Q}={\{q:\mathcal{X}\rightarrow\mathbb{R}:q(\mathbf{x})=\mathbf{q}\prime\mathbf{x}=\sum_{j=1}^p q^jx^j}\}. Q={q:X→R:q(x)=q′x=j=1∑p​qjxj}.

以经验风险作为优化目标，当$p$相对小时，目标函数可表示为 (NV-ERM1)
$$\underset{q:q(\mathbf{x})={\sum }_{j=1}^p{q}^j{x}^j}{\min }\hat{R}(q(.);S_n)=\frac{1}{n}\sum _{i=1}^n[b(d_i-q({\mathbf{x}}_i{)}^{+}+h(q({\mathbf{x}}_i)-d_i{)}^{+}];$$

相反，当$p$相对大时($p\ge n$)，加入正则项为 (NV-ERM2)：
$$\underset{q:q(\mathbf{x})={\sum }_{j=1}^p{q}^j{x}^j}{\min }\hat{R}(q(.);S_n)=\frac{1}{n}\sum _{i=1}^n[b(d_i-q({\mathbf{x}}_i{)}^{+}+h(q({\mathbf{x}}_i)-d_i{)}^{+}]+\lambda \Vert \mathbf{q}{\Vert }_k^2,$$

其中$\lambda >0$为正则系数，$||\mathbf{q}|{|}_k$表示向量$\mathbf{q}=[q^1,\dots ,q^p]$的${\ell }_k$范数。若以${\ell }_2$为正则范数，则问题转化为二阶锥规划。若可预测需求很小，则可以使用${\ell }_0$半范数或 ${\ell }_1$范数 来增大系数向量的稀疏性，进而问题转化为MILP 或 LP。NV-ERM1 和 NV-ERM2 的完整模型可参考原文或下图。

KO 算法

给定历史数据$({\mathbf{x}}_1,y_1),\dots ,({\mathbf{x}}_n,y_n)$，Nadaraya and Watson 提出局部加权平均来估计$m({\mathbf{x}}_{n+1})=\mathbb{E}[Y|{\mathbf{x}}_{n+1}]$:
$$m_h({\mathbf{x}}_{n+1})=\frac{{\sum }_{i=1}^n{K}_w({\mathbf{x}}_{n+1}-{\mathbf{x}}_i)y_i}{{\sum }_{i=1}^n{K}_w({\mathbf{x}}_{n+1}-{\mathbf{x}}_i)},$$

其中$K_w(.)$是具有带宽$w$的核函数。现对于订购量$q$, 在观察特征${\mathbf{x}}_{n+1}$之后的特征相关报童期望成本可表示为$\mathbb{E}[C(q;D)|{\mathbf{x}}_{n+1}]$; 因此，如果将报童成本视为因变量，可以通过 Nadaraya-Watson 方法进行估计，即
$$\frac{{\sum }_{i=1}^n{K}_w({\mathbf{x}}_{n+1}-{\mathbf{x}}_i)C(q;d_i)}{{\sum }_{i=1}^n{K}_w({\mathbf{x}}_{n+1}-{\mathbf{x}}_i)}.$$
文章将以上针对特征数据驱动的报童模型的方法称为核优化 (NV-KO), 即
$$\underset{q\ge 0}{\min }\tilde{R}(q;S_n,{\mathbf{x}}_{n+1})=\underset{q\ge 0}{\min }\frac{{\sum }_{i=1}^n{K}_w({\mathbf{x}}_{n+1}-{\mathbf{x}}_i)C(q;d_i)}{{\sum }_{i=1}^n{K}_w({\mathbf{x}}_{n+1}-{\mathbf{x}}_i)},$$

为一维分段线性优化问题，其最优报童模型决策${\hat{q}}_n^k$为
q ^ n k = q ^ n k ( x n + 1 ) = inf ⁡ { q : ∑ i = 1 n k i I ( d i ≤ q ) ∑ i = 1 n k i ≥ b b + h } , \hat{q}_n^k=\hat{q}_n^k(\mathbf{x}_{n+1})=\inf{\{q:\frac{\sum_{i=1}^n\mathcal{k}_i\mathbb{I}(d_i\leq{q})}{\sum_{i=1}^n\mathcal{k}_i}\geq }\frac{b}{b+h}\}, q^​nk​=q^​nk​(xn+1​)=inf{q:∑i=1n​ki​∑i=1n​ki​I(di​≤q)​≥b+hb​},

其中$k_i=K_w({\mathbf{x}}_{n+1}-{\mathbf{x}}_i).$

截止文章发表为止，在库存决策中纳入外源信息的算法还包括：Liyanage and Shanthikumar (2005) 的操作统计 (Operational Statistics, OS)、See and Sim（2010）通过考虑线性决策规则以及分段线性决策规则来解决鲁棒问题、Hannal et al. (2010) 的周期随机优化问题。在原文的实例研究中，文章考虑了使用操作统计学启发式特征，结合NV-ERM1 和2， 在有无特征的情况下进行求解并进行比较。

特征信息的价值（问题二）

文章通过将 NV-ERM1 决策与仅根据过去的需求数据做出的 SAA 决策进行比较，量化在报童决策中纳入特征的价值。 考虑两种需求模型，两群体需求模型和线性需求模型：在这两种情况下，文章通过理论证明（原文引理1和引理2, 定理1,2,3），**SAA决策产生不一致的决策，而基于特征的判定是一致的；进一步量化对预期成本的影响，对于远离真正最优的决策来说，预期成本必然更大。**简述如下：

两群体需求模型 $$D=D_0(1-x)+D_{1}x$$

• NV-ERM1 最优订货量为

q ^ n 0 = inf ⁡ { q : F ^ 0 ( q ) ≥ b b + h } = d ( ⌈ n 0 r ⌉ ) 0 , if  x n + 1 = 0 ; \hat{q}^0_n=\inf\{q:\hat{F}_0(q)\geq \frac{b}{b+h}\}=d^0_{(\lceil{n_0r}\rceil)},\qquad \text{if }x_{n+1}=0; q^​n0​=inf{q:F^0​(q)≥b+hb​}=d(⌈n0​r⌉)0​,if xn+1​=0;

q ^ n 1 = inf ⁡ { q : F ^ 1 ( q ) ≥ b b + h } = d ( ⌈ n 1 r ⌉ ) 1 , if  x n + 1 = 1. \hat{q}^1_n=\inf\{q:\hat{F}_1(q)\geq \frac{b}{b+h}\}=d^1_{(\lceil{n_1r}\rceil)},\qquad \text{if }x_{n+1}=1. q^​n1​=inf{q:F^1​(q)≥b+hb​}=d(⌈n1​r⌉)1​,if xn+1​=1.

即${\hat{q}}_n^0$ 用于解决 $x=0$对应的数据子样本SAA问题，而${\hat{q}}_n^0+{\hat{q}}_n^1$用于解决解决 $x=1$对应的数据子样本SAA问题。

• NV-ERM1的有限样本偏差和渐近最优性：基于特征的决策的有限样本决策的偏差最多为$\mathcal{O}(\log n_i/n_i),i=1,2$:

$$|\mathbb{E}[{\hat{q}}_n^i]-F_0^{-1}(r)|\le \mathcal{O}(\frac{\log n_i}{n_i}),i=0,1.$$

基于特征的决策是渐近最优的，随着观测值数量趋于无穷大，其可以正确识别$x=0$ 或$1$的具体情况。

$$\underset{n\to \infty }{\lim }{\hat{q}}_n^i\stackrel{a.s.}{=}{F}_0^{-1}(r)=:q_i^{\ast },i=0,1$$

• SAA 最优订货量为

q ^ n S A A = inf ⁡ { q : F ^ n m i x ( q ) ≥ b b + h } = d ( ⌈ n r ⌉ ) . \hat{q}^{SAA}_n=\inf\{q:\hat{F}^{mix}_n(q)\geq \frac{b}{b+h}\}=d_{(\lceil{nr}\rceil)}. q^​nSAA​=inf{q:F^nmix​(q)≥b+hb​}=d(⌈nr⌉)​.

• SAA 的有限样本偏差和渐近（sub）最优性：平均而言，如果在下一个决策周期内$x=0$，则SAA决策命令过多，如果$x=1$，则SAA决策命令过少。并且 SAA 决策不是渐近最优的（不一致），也就是说，即使有无限量的需求数据，无特征的 SAA 决策也会收敛到与真实最优值不同的数量。

线性需求模型 $D|(\mathbf{X}=\mathbf{x})={\beta }^T\mathbf{x}+ϵ$$, $$ϵ\sim F_{ϵ}$与特征向量 $\mathbf{X}$独立。

• SAA与DM2的订购量 ${\hat{q}}^{SAA}$, ${\hat{q}}^{DM2}$分别为

q ^ S A A ( x n + 1 ) = inf ⁡ { y : F ^ n 0 ( y ) ≥ b b + h } + d ˉ n \textstyle\hat{q}^{SAA}(\mathbf{x}_{n+1}) = \inf\{y: \hat{F}_n^0(y)\geq \frac{b}{b+h}\}+\bar{d}_n q^​SAA(xn+1​)=inf{y:F^n0​(y)≥b+hb​}+dˉn​

q ^ D M 2 ( x n + 1 ) = inf ⁡ { y : F ^ n 2 ( y ) ≥ b b + h } + ∑ k = 2 p q ^ k x n + 1 k \textstyle\hat{q}^{DM2}(\mathbf{x}_{n+1}) = \inf\{y: \hat{F}_n^2(y)\geq \frac{b}{b+h}\}+\sum_{k=2}^p\hat{q}^kx_{n+1}^k q^​DM2(xn+1​)=inf{y:F^n2​(y)≥b+hb​}+∑k=2p​q^​kxn+1k​

其中${\hat{F}}_n^2$是 { d i − ∑ k = 2 p q ^ k x i k } \{d_i-\sum_{k=2}^{p}\hat{q}^kx_i^k\} {di​−∑k=2p​q^​kxik​}的经验分布，且${\hat{q}}^k,$ $k=2,\dots ,p$是NV-ERM1解的系数。

• 没有特征会导致不一致的决策

$${\hat{q}}_n^{SAA}(\tilde{\mathbf{x}})\stackrel{a.s.}{\to }{Q}_{ϵ}(\frac{b}{b+h})+{\mathbb{E}}_{\mathbf{x}}[{\mathbb{E}}_{ϵ}[D|\mathbf{X}]]=Q_{ϵ}(\frac{b}{b+h})+{\beta }^T\mathbb{E}[\mathbf{X}]$$

$${\hat{q}}_n^{DM2}(\tilde{\mathbf{x}})\stackrel{a.s.}{\to }{Q}_{ϵ}(\frac{b}{b+h})+{\beta }^T\tilde{\mathbf{x}}=q^{\ast }(\tilde{\mathbf{x}})$$

SAA决策收敛于离散度$\epsilon$加上总体时间平均需求的临界分位数${\mathbb{E}}_{\mathbf{X}}[{\mathbb{E}}_{\epsilon }[D|\mathbf{X}]]$，而DM2的决策收敛到正确的决策$q^{\ast }(\tilde{\mathbf{x}})$。由SAA的不一致性产生一个问题：就预期成本而言，远离真正最优的决策必然更差吗？ 换句话说，当特征信息的效果增加时，预期成本的损失是否会增加？

• 预期成本差值。 原文通过定理4证明，设$q^{\ast }=q^{\ast }(\tilde{\mathbf{x}})$表示基于特征$\tilde{\mathbf{x}}$和非最优解$\hat{q}$的报童模型最优解，则两个决策所产生的成本差值为

  $$\mathbb{E}C(\hat{q};D)-\mathbb{E}C(q^{\ast };D)=(b+h)\mathbb{E}[|\hat{q}-D|\mathbb{I}\{(\hat{q}\vee q^{\ast })\le D\le (\hat{q}\vee q^{\ast })\}].$$

观察到预期成本差值随$|\hat{q}-D|$的期望在两个决策之间$\hat{q}$与$q^{\ast }$的区间上变化。预期成本差异随着$\hat{q}$偏离$q^{\ast }$而增加。差异的大小与该区间长度以及需求在该区间上的分布情况相关，分布越集中，差异就越大。

尽管上述结论证明了特征集合的合理性，但一个缺点是，决策者需要知道需求分布以量化次优样本内决策所带来的预期成本增益，但事实不尽如此。文章随后使用现有信息以高概率范围，来描述决策者的样本内决策的预期成本。

使用样本内信息的样本外成本界限（问题三）

文章对 NV-ERM1、NV-ERM2 和 NV-KO 选择的排序决策的样本外成本提供理论保证，目标是提供可利用现有数据计算的性能界限。我们看到性能界限分为两个部分：一个与有限数据量产生的偏差有关，通常称为有限样本偏差，另一个与样本内决策的方差有关，称为泛化误差。

术语“泛化”是指样本内决策对样本外数据的泛化能力，并且是过度拟合程度的度量，因为泛化误差较大的决策与较大的过度拟合相关。 过度拟合的决策可能会产生误导； 例如，如果样本内决策的选择有很大的自由度，那么样本内成本可能为零，导致决策者认为完美排序是可能的。然而，精明的决策者如果意识到过度拟合的危险，就会谨慎地仅根据样本内数据得出结论，而泛化误差为决策者的决策提供了过度拟合如何产生的描述。

定义“真实风险”为样本外风险，其中期望关于某未知分布$\mathcal{X}\times \mathcal{D}$, $\mathcal{X}\subset {\mathbb{R}}^p$:

$$R_{true}(q):={\mathbb{E}}_{D(\mathbf{x})}[C(q;D(\mathbf{x}))]$$

定义经验风险为训练样本的平均成本：

$$\hat{R}(q;S_n):=\frac{1}{n}\sum _{i=1}^{n}C(q,d_i({\mathbf{x}}_i))$$

经验风险可以计算，而真实风险则不能； 然而仅凭经验风险并不能完整地反映真实风险。 基于三点假设（详见原文4.1）文章提供了关于真实风险的概率上界，其与经验风险和算法稳定性方法相关。 定理5-7的假设见原文第4节。

• NV-ERM1的样本外性能（原文定理5）：样本内决策成本与真正最优决策的预期成本的差值绝对值

  $|R_{true}(q^{\ast })-{\hat{R}}_{in}(\hat{q};S_n)|$

  $$\le (b\vee h)\bar{D}[\frac{2(b\vee h)}{b\wedge h}\frac{p}{n}+(\frac{4(b\vee h)}{b\wedge h}p+1)\sqrt{\frac{\log (2/\sigma )}{2n}}]$$

  $$+(b\vee h)K\frac{\sqrt{\log n}}{n^{1/(2+p/2)}}$$

  其中 $K=\sqrt{\frac{9(8+5p)}{(4+p)}}\frac{1}{(1-2^{-4/(4+p)}){\lambda }_2^{\ast }}$, ${\lambda }_2^{\ast }={\min }_{t\in [\underline{D},\bar{D}]}{f}_{\epsilon }(t)$, $n\ge 3.$

• 右侧上界的第一项是泛化误差的界，泛化误差是样本内决策的训练误差和测试误差之间的差。对于固定成本参数 b 和 h，我们发现泛化误差为$O(p/\sqrt{n})$。因此，如果总体模型中的相关特征的数量很小，并且相对于观测值的数量不增长，则样本内决策可以很好地推广到样本外数据。换句话说，过拟合不应该是问题。关于进一步的细节，请参考附录C和Bousquet和Elisseeff（2002）中的证明。右侧上界的第二项是由于 $\mathbb{E}[q^{\ast }-\hat{q}]$ 的有限样本偏差。关于细节，请参考附录C中定理5的证明。

• NV-ERM2的样本外性能（原文定理6）：在上式基础上引入正则项

  $|R_{true}(q^{\ast })-{\hat{R}}_{in}(\widehat{q_{\lambda }};S_n)|$

  $$\le (b\vee h)\bar{D}[\frac{(b\vee h)X_{max}^{2}p}{n\lambda \bar{D}}+(\frac{2(b\vee h)X_{max}^{2}p}{\lambda \bar{D}}+1)\sqrt{\frac{\log (2/\sigma )}{2n}}]$$

  $$+(b\vee h){\mathbb{E}}_{D|{\mathbf{x}}_{n+1}}[|{\hat{q}}_{\lambda }-\hat{q}|]+(b\vee h)K\frac{\sqrt{\log n}}{n^{1/(2+p/4)}}$$

  其中 $K=\sqrt{\frac{9(8+5p)}{(4+p)}}\frac{1}{(1-2^{-4/(4+p)}){\lambda }_2^{\ast }}$, ${\lambda }_2^{\ast }={\min }_{t\in [\underline{D},\bar{D}]}{f}_{\epsilon }(t)$, $n\ge 3.$

第一项是泛化误差的界，其为$\mathcal{O}(p/\lambda \sqrt{n})$。因此，过拟合的量可以通过施加在问题上的正则化的量来直接控制，λ越大，泛化误差越小。其中不等式右侧第二项其未出现在定理5中，是由于正则化引起的样本内决策的偏差。对于较大的 λ，该项较大，因此在泛化误差和正则化偏差之间存在折衷。第三项也是最后一项是有限样本偏差。虽然正则化偏差可以通过 λ 来控制，但有限样本偏差只能通过收集更多的数据来控制。

• NV-KO 的样本外性能（原文定理7）：

  $|R_{true}(q^{\ast })-{\hat{R}}_{in}(\hat{q};S_n)|$

  $\le (b\vee h)\bar{D}[\frac{2(b\vee h)}{b\wedge h}\frac{1}{1+(n-1)r_w(p)}$

  $+(\frac{4(b\vee h)}{1/n+(1-1/n)r_w(p)}+1)\sqrt{\frac{\log (2/\sigma )}{2n}}]$

  $+(b\vee h){\mathbb{E}}_{D|{\mathbf{x}}_{n+1}}[|{\hat{q}}^k-\hat{q}|]+(b\vee h)K\frac{\sqrt{\log n}}{n^{1/(2+p/2)}}$

其中$r_w(p)=\exp (-2X_{max}^{2}p/w^2)$, $w$ 为核函数的带宽, $K=\sqrt{\frac{9(8+5p)}{(4+p)}}\frac{1}{(1-2^{-4/(4+p)}){\lambda }_2^{\ast }}$, ${\lambda }_2^{\ast }={\min }_{t\in [\underline{D},\bar{D}]}{f}_{\epsilon }(t)$, $n\ge 3.$

关于 NV-KO 的性能界限具有三个分量：泛化误差的界限，当真实决策是函数时由于用数量决策优化而导致的偏差，以及有限样本偏差项。泛化误差为$\mathcal{O}(1/r_w(p)\sqrt{n})$，因此可以通过增加核带宽 $w$ 来降低 $r_w(p)$ 进行控制。然而，与NV-ERM 2一样，增加的 $w$ 增加了第二项误差，因此在实践中 $w$ 需要在合理的值范围内优化。有限样本偏差项与定理5-6中的相应项起着相同的作用。

实例研究：急诊室护士排班问题（问题四）

文章通过医院急诊室的护士配置问题，即医院在某一天应该安排多少个护士，应用这三种算法 (NV-ERM1, NV-ERM2, NV-KO)，以找到最佳的医院急诊室护士的人员配置水平。由于发达国家的大多数医院都规定或建议最低护士与患者的比例，近似护士配备问题作为一个报童问题，护士人员配备问题是测试文章介绍的数据驱动模型的自然环境。

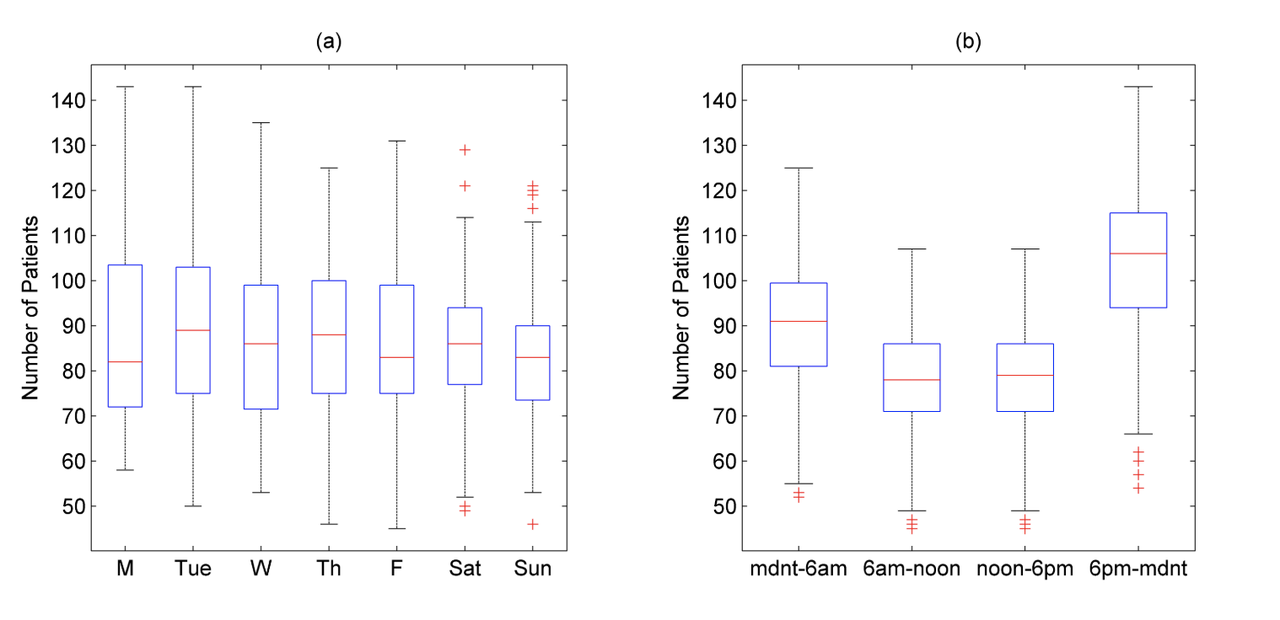
文章的数据来自2008年7月至2009年6月英国一家大型教学医院的急诊室。数据集包括以2小时间隔在急诊室中的患者总数。在图1中提供了按天和按时间段的患者数量的箱形图。数据显示病人的数量与时间有一定的相关性。详情请见原文第五节。

假设护士与病人的比例为$1:5$，机构护士的小时工资是正规护士的2.5倍，$b=2.5/3.5$, $h=1/3.5$，目标分位数为$r=2.5/3.5$。考虑两组特征：

• 第一组是每周某天，每天某时，以及记录过去需求的天数$m$;

• 第二组是第一组的样本加上过去需求的样本平均值和过去需求的顺序统计量的差（操作统计(OS)特征，详见 Liyanage and Shanthikumar, 2005）.

文章使用$n=1344$个历史需求观察（16周）作为训练数据，并计算3个周期前的关键人员配备水平。然后，在 $1344/2=672$ 验证数据上记录预计人员配置水平的样本外报童成本。文章所考虑的16种不同方法及缩写如下表所示。

表1：方法汇总

表2 汇总了文章所考虑的 16 种方法的样本外表现，其中包括校准参数 (calibrated parameter)、平均计算时间（秒）、均值、95% 置信区间（详见原文附录表 EC.1–EC.7)，以及该方法的年度节省成本。

表2：结果汇总

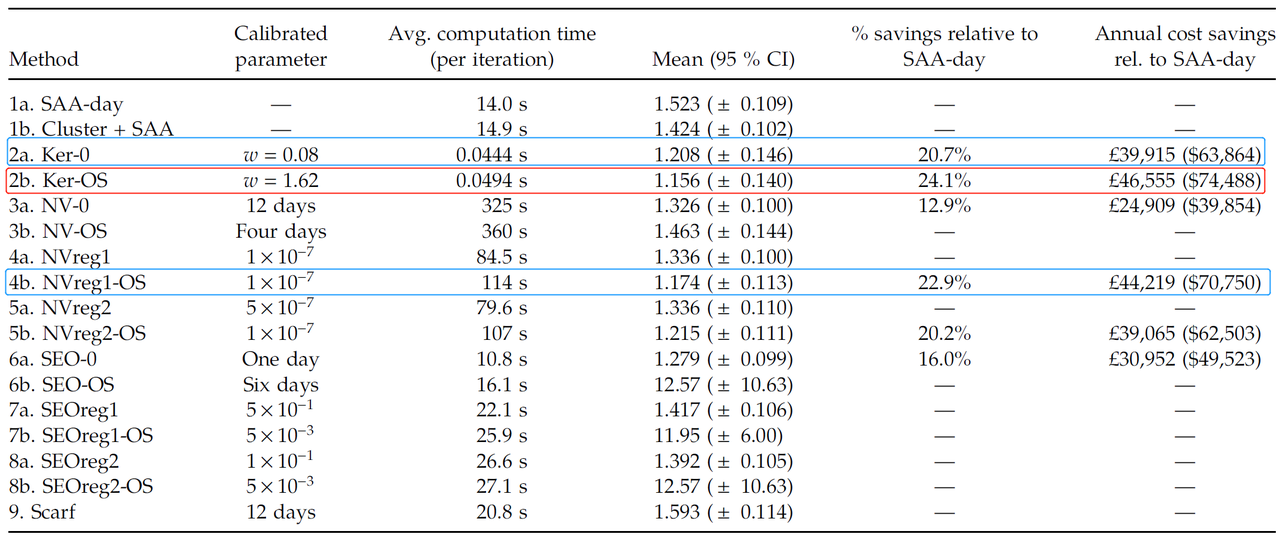
以上结果中，最佳结果通过采用带宽 $w=1.62$ 的 KO 方法获得，其相对于最佳实践基准（“SAA 天”），成本改善了 24%（每年节省 46,555 英镑），具有5%的统计显著性在水平。次好结果是采用 ${\ell }_1$正则化的 ERM 方法和不考虑 OS 特征的 KO 方法，其平均年成本分别降低了 23%（每年 44,219 英镑）和 21%（每年 39,915 英镑）。

然而，基于特征的方法的计算成本非常不同。 KO 方法比基于 ERM 的方法快三个数量级。 例如，使用具有 OS 特征的 KO 方法仅需 0.0494 秒即可找到下一个最佳人员配置水平，而采用${\ell }_1$正则化的 ERM 方法则需要 114 秒。

实践见解

1. 没有单一的方法可以解决大数据报童问题。 文章提出了三种使用特征需求数据集的方法，并与使用或不使用特征来解决问题的许多其他潜在方法进行了比较。 这并不是说这些方法是详尽无遗的。 我们对开发新方法持乐观态度。
2. 大数据驱动的决策者总是需要警惕过度拟合，因为决策在样本内表现良好，但在样本外则不然，因此，不仅会导致决策表现不佳，还会导致决策失败。 文章已经证明，过拟合可以通过先验特征选择或正则化来控制，这为决策者提供了额外的控制权，使决策有利于改进样本外泛化。
3. 影响样本内决策真实性能的因素包括泛化误差（又名过度拟合误差）、正则化带来的偏差以及仅因数据量有限而产生的有限样本偏差。 决策者可以通过正则化参数控制正则化产生的泛化误差和偏差，在实践中，需要在单独的验证数据集上对一系列参数值进行优化。 除非收集更多数据，否则无法控制有限样本偏差。
4. 尽管在文章的案例研究中，KO 方法在样本外性能方面优于所有其他方法，但对于不同的数据集，情况不一定如此。 我们认为，案例研究最重要的一点是展示如何进行仔细的数据驱动调查，而不是针对具体案例得出 KO 方法表现最佳的结论。 然而，我们注意到 KO 方法的相对速度是可以推广的。

参考文献

Bousquet, Olivier, André Elisseeff. 2002. Stability and generalization. The Journal of Machine Learning.
Liyanage LH, Shanthikumar JG (2005) A practical inventory control policy using operational statistics. Oper. Res. Lett. 33(4):341–348.
Nadaraya EA (1964) On estimating regression. Theory Probab. Appl. 9(1):141–142.
See C-T, Sim M (2010) Robust approximation to multiperiod inventory management. Oper. Res. 58(3):583–594.
Vapnik VN (1998) Statistical Learning Theory (Wiley, New York).
Watson GS (1964) Smooth regression analysis. Sankhya: Indian J. Statist. Ser. A. 26(4):359–372.