1.Hash基础
(1)基础
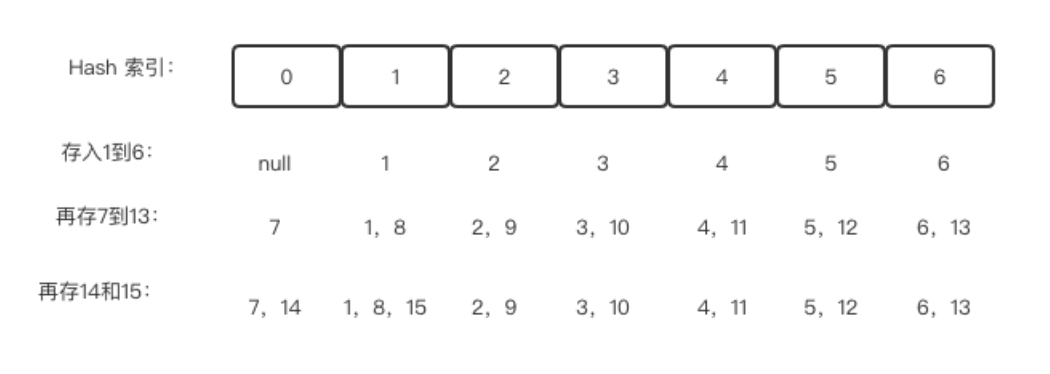
哈希也称为散列,通过算法变成固定长度的输出值,存入对应的位置
例如这个算法为取模算法,index=number 模 7
存入1到15
(2)碰撞处理
当多个元素映射到同一位置上时就产生了碰撞
哈希碰撞处理是在使用哈希函数时,不同的键可能映射到相同的哈希值(哈希冲突)时的解决方法。哈希碰撞处理是为了确保不同的键可以在哈希表中正确存储和检索,从而维护哈希表的性能和正确性。
以下是几种常见的哈希碰撞处理方法:
链地址法(Chaining): 这是一种常见的方法,通过在哈希桶位置上维护一个链表(或其他数据结构),将发生冲突的键值对添加到链表中。在查找或删除操作时,遍历链表来找到对应的键值对。
开放定址法(Open Addressing): 在这种方法中,当发生冲突时,会顺序地在哈希表中的其他位置寻找空闲的位置来存储键值对。这包括线性探测、二次探测、双重哈希等策略。
再哈希法(Rehashing): 当发生冲突时,计算另一个哈希函数,然后将键值对存储在新的哈希桶位置上。这可以有效地减少冲突。
建立一个“桶”的链表: 这是一种类似于链地址法的方法,但不是在每个哈希桶位置上维护一个链表,而是在发生冲突的哈希桶位置上维护一个链表。
完全二叉树: 将键值对按照哈希值顺序存储在完全二叉树的节点上。这种方法在特定情况下可以提供较好的性能。
开放定址法
开放定址法的主要思想是,当发生哈希冲突时,不仅仅将数据存储在哈希桶中,而是根据某种算法找到一个不冲突的位置,将数据存储在那里。这就需要一个探测序列(probing sequence),它是一系列指示位置的步骤,用于寻找下一个可用的位置。
常见的开放定址法包括:
-
线性探测(Linear Probing): 在发生冲突时,按顺序检查下一个位置,直到找到一个空闲位置为止。
-
二次探测(Quadratic Probing): 在发生冲突时,按照某个步长的平方逐渐增加位置,直到找到一个空闲位置为止。
-
双重散列(Double Hashing): 在发生冲突时,使用第二个哈希函数计算一个步长,然后在哈希表中逐渐增加位置,直到找到一个空闲位置为止。
开放定址法的优点是它对于内存的利用更有效,因为数据存储在数组中,没有额外的指针。然而,它在负载因子高时可能会导致聚集现象(clustering),即一些位置上会有很多连续的元素,而其他位置则很少使用。这可能会降低性能。
链地址法
"链地址法"(Chaining)是一种哈希表解决哈希冲突的方法之一。在哈希表中,不同的键可能会映射到相同的哈希桶位置,这就产生了哈希冲突。链地址法通过在每个哈希桶位置上维护一个链表(或其他数据结构)来处理这种冲突。
具体来说,当发生哈希冲突时,链地址法将冲突的键值对添加到哈希桶位置对应的链表中。每个链表节点包含一个键值对。当需要插入、查找或删除一个键值对时,先计算哈希值找到对应的哈希桶位置,然后在该位置的链表中进行操作。
以下是链地址法的基本步骤:
-
插入: 计算键的哈希值,找到对应的哈希桶位置。如果该位置为空,则在该位置插入键值对。如果该位置已经有其他键值对存在(即发生冲突),则在链表中继续插入新的键值对。
-
查找: 计算键的哈希值,找到对应的哈希桶位置。然后遍历链表,查找包含该键的节点。
-
删除: 计算键的哈希值,找到对应的哈希桶位置。然后遍历链表,找到包含该键的节点,并进行删除操作。
链地址法的优点是它相对简单,可以有效地解决哈希冲突。然而,当哈希冲突较多时,链表可能会变得较长,导致操作的时间复杂度增加。为了保持哈希表的高效性能,需要根据数据分布情况来选择合适的哈希函数,并根据情况动态调整哈希桶的数量。另外,当链表过长时,可以考虑使用更高效的数据结构,如红黑树,来替代链表,以提高查找效率。
2.队列基础
FIFO先进先出的线性表
基于链表实现
尾插+头删
public class MyLinkQueue {
static class Node {
public int data;
public Node next;
public Node(int data) {
this.data = data;
}
}
private Node front;
private Node rear;
private int size;
//无参构造初始化
public MyLinkQueue() {
this.front = null;
this.rear = null;
}
public boolean isEmpty() {
return front == null;
}
//尾插
public void push(int data){
Node node = new Node(data);
if (isEmpty()){
front = node;
rear = node;
}else{
rear.next = node;
rear = node;
}
size++;
}
//头删
public int pop(){
if (isEmpty()){
throw new EmptyStackException();
}
int res = front.data;
front = front.next;
size--;
return res;
}
public int size(){
return size;
}
public void traverse(){
Node t = front;
while(t!=null){
System.out.println(t.data);
t = t.next;
}
}
public static void main(String[] args) {
MyLinkQueue queue = new MyLinkQueue();
queue.push(10);
queue.push(20);
queue.push(30);
System.out.println("Queue elements:");
queue.traverse(); // Output: 10 20 30
System.out.println("Dequeued element: " + queue.pop()); // Output: 10
System.out.println("Queue size: " + queue.size()); // Output: 2
queue.push(40);
queue.push(50);
System.out.println("Queue elements:");
queue.traverse(); // Output: 20 30 40 50
System.out.println("Queue size: " + queue.size()); // Output: 4
}
}