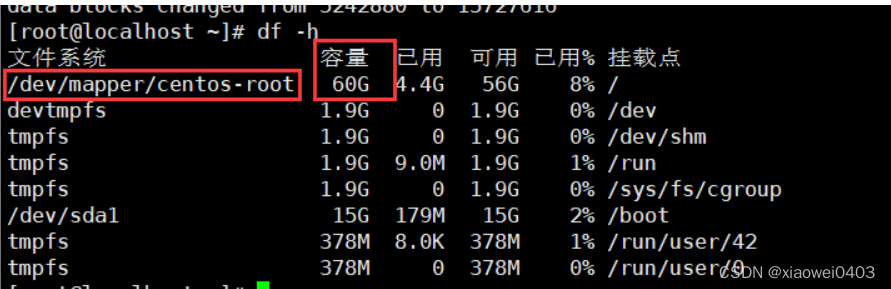
来源:“范式杯”2023牛客暑期多校训练营10 —— L Grayscale Confusion
题意:给定
n
个三元组
(
r
i
, g
i
, b
i
)
。构造一个长度为
n
的数组 w, 使得
①w1
=
w
2
②对于任意 i, j
,若
r
i
> r
j
, g
i
> g
j
, b
i
> b
j
,则
w
i
> w
j
输出任意合法构造均可。
思路:
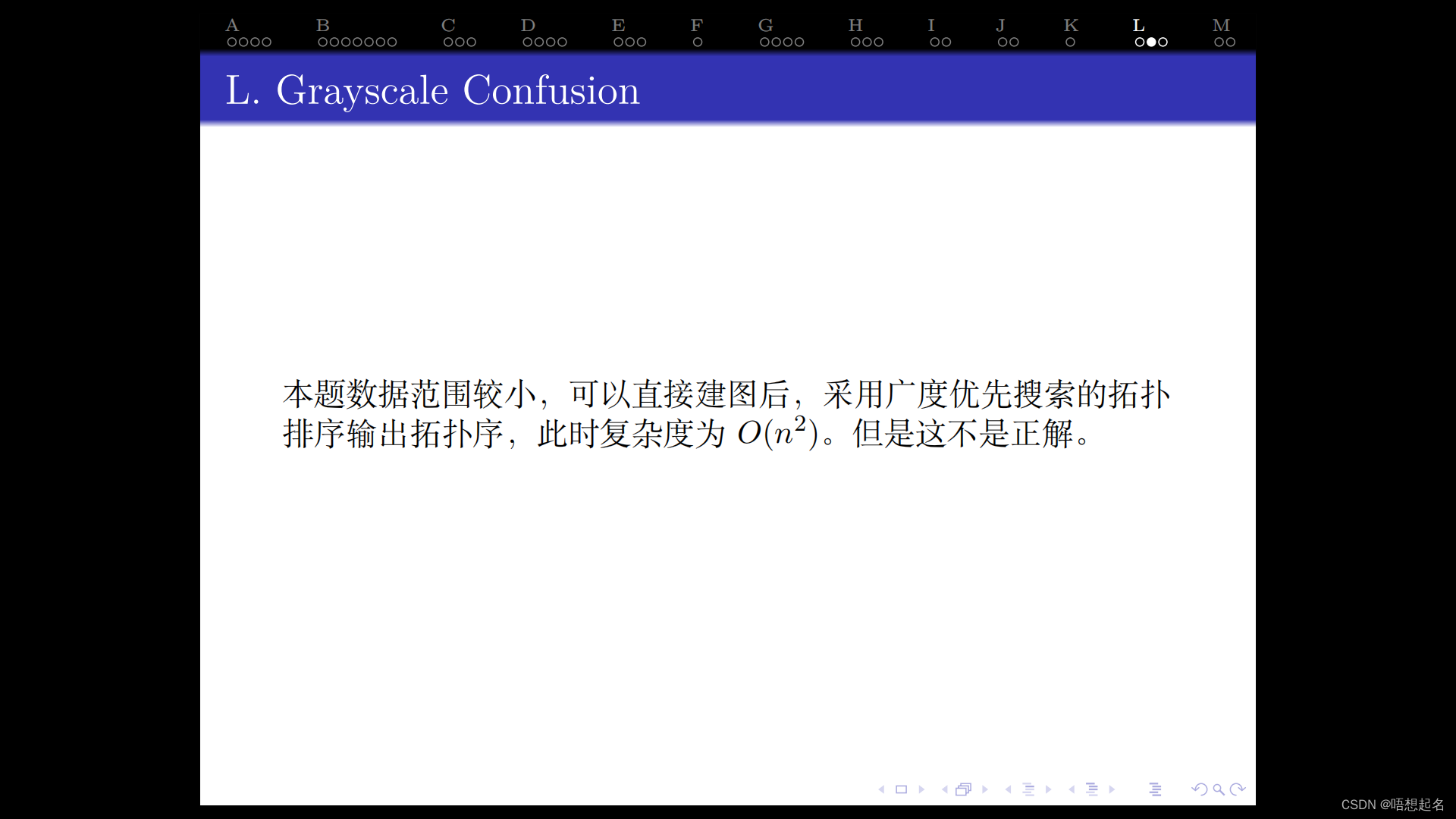
AC代码:
#include<bits/stdc++.h>
using namespace std;
int n, r[1005], g[1005], b[1005], in[1005], q[1005], hh = 0, tt = -1, ans[1005];
int e[1000005], ne[1000005], h[1000005], idx;
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool small(int x, int y){
return r[x]<r[y] && g[x]<g[y] && b[x]<b[y];
}
signed main(){
memset(h, -1, sizeof h);
cin>>n;
for(int i = 0; i<n; ++i)
scanf("%d %d %d", &r[i], &g[i], &b[i]);
if(small(0,1) || small(1,0)){
printf("-1");
return 0;
}
for(int i = 2; i<n; ++i){
for(int j = 2; j<n; ++j)
if(small(i,j)) add(i,j), in[j]++;
if(small(i,0) || small(i,1)) add(i,1), in[1]++;
if(small(0,i) || small(1,i)) add(1,i), in[i]++;
}
for(int i = 1; i<n; ++i)
if(in[i]==0) q[++tt] = i;
while(hh<=tt){
int t = q[hh++];
for(int i = h[t]; i!=-1; i = ne[i]){
int j = e[i];
if(--in[j] == 0){
q[++tt] = j;
}
ans[j] = max(ans[j], ans[t]+1);
}
}
ans[0] = ans[1];
for(int i = 0; i<n; ++i) printf("%d\n", ans[i]);
return 0;
}