A 统计和小于目标的下标对数目
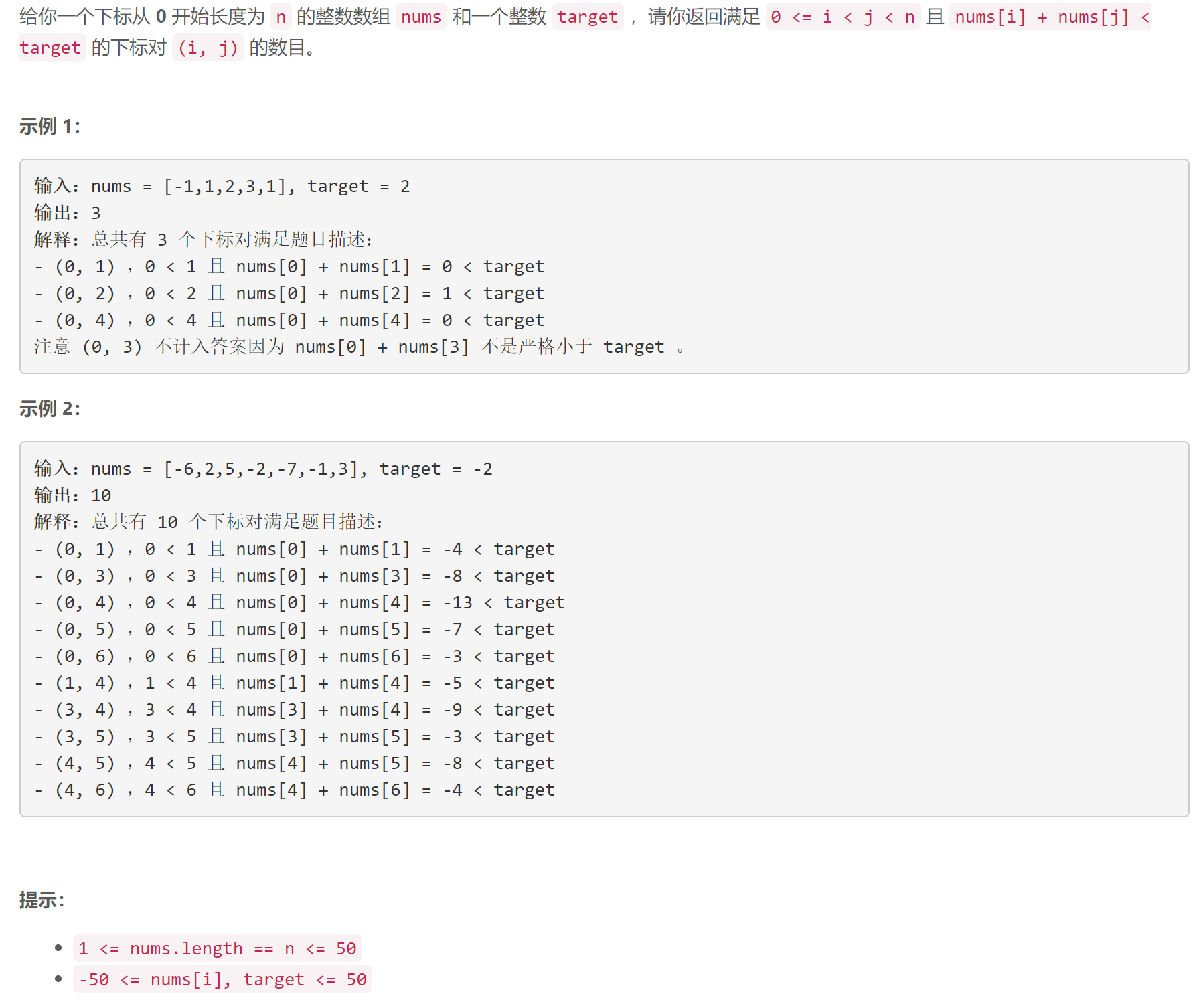
数据量小,直接枚举数对
class Solution {
public:
int countPairs(vector<int> &nums, int target) {
int n = nums.size();
int res = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < i; j++)
if (nums[i] + nums[j] < target)
res++;
return res;
}
};
B 循环增长使字符串子序列等于另一个字符串
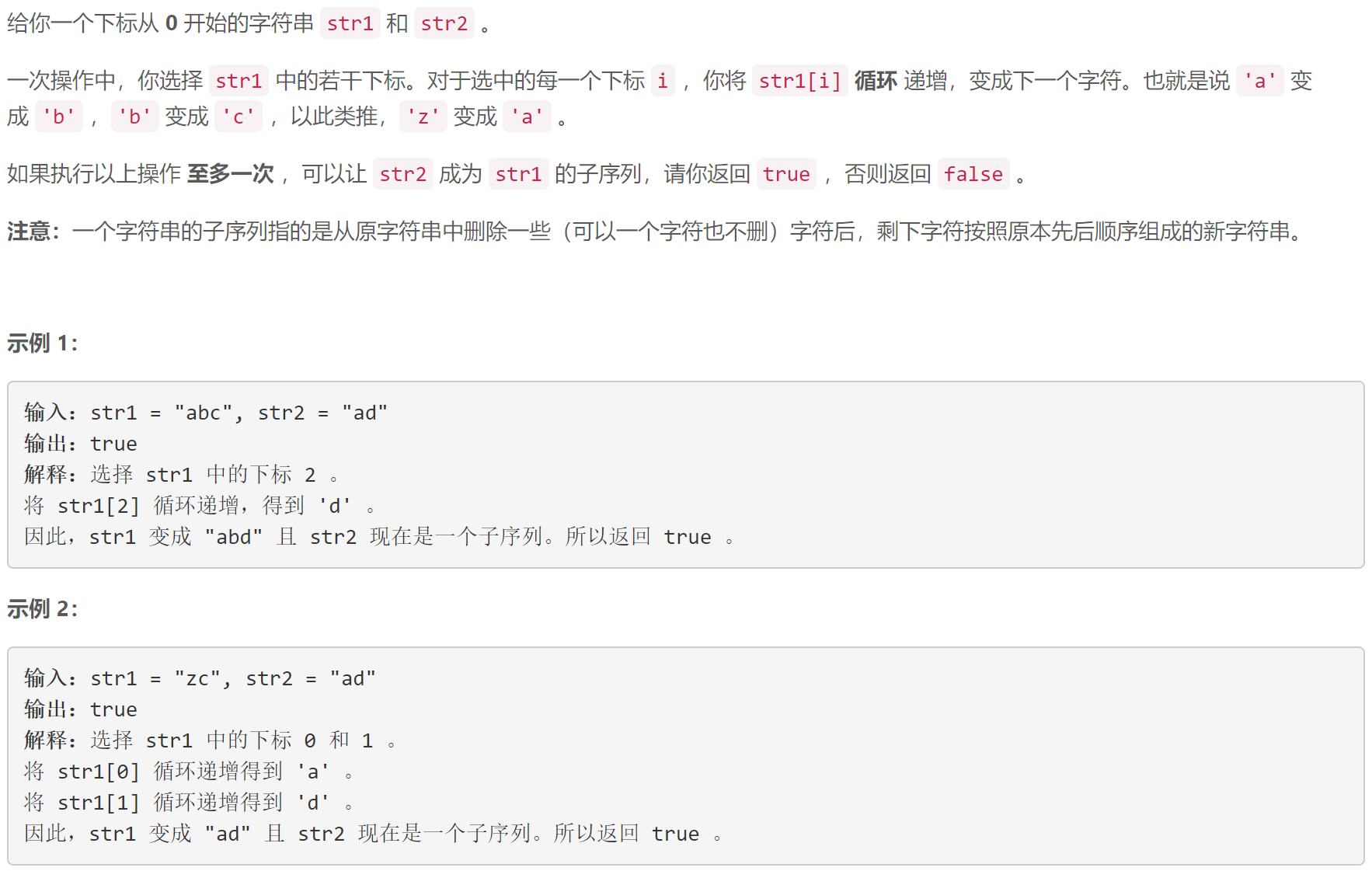
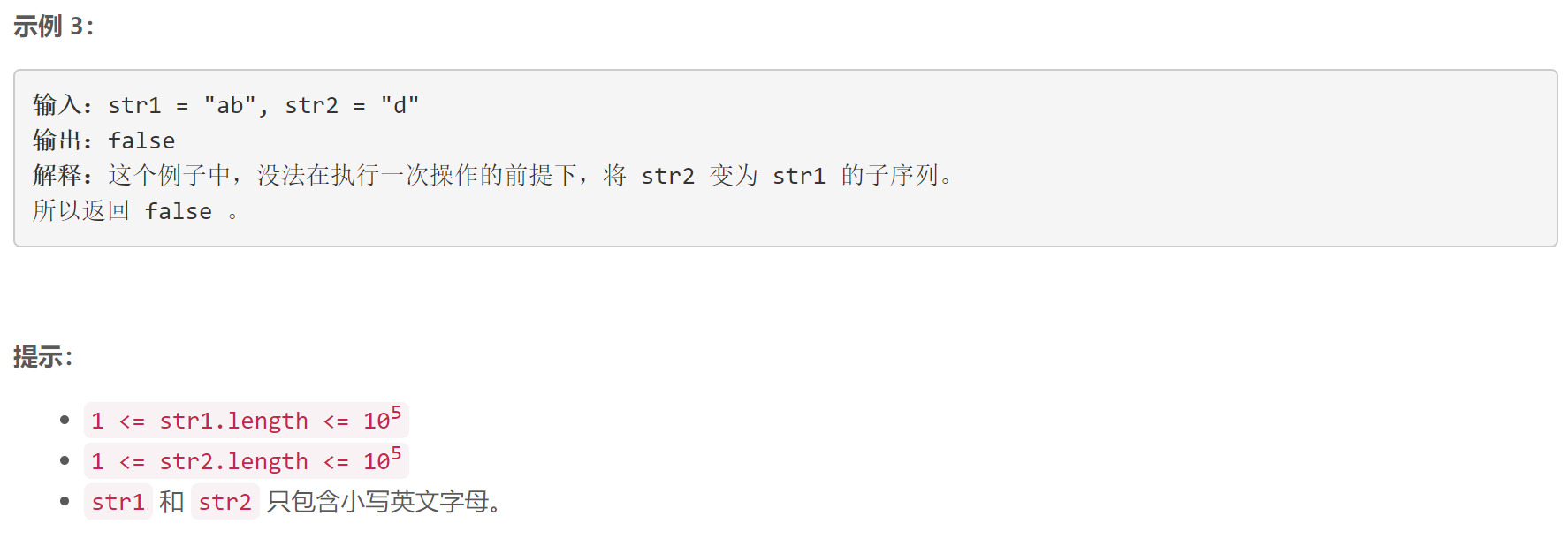
贪心:从两字符串的头部开始匹配,若两串中的字符匹配则两串中的下标都+1,否则仅
str1中的下标+1,最终通过str2中的下标判断str2是否已匹配完。
class Solution {
public:
bool canMakeSubsequence(string str1, string str2) {
int m = str1.size(), n = str2.size();
int i = 0, j = 0;
for (; i < m && j<n;) {
if (str1[i] == str2[j] || ('a' + (str1[i] - 'a' + 1) % 26) == str2[j]) {
i++;
j++;
} else {
i++;
}
}
return j == n;
}
};
C 将三个组排序

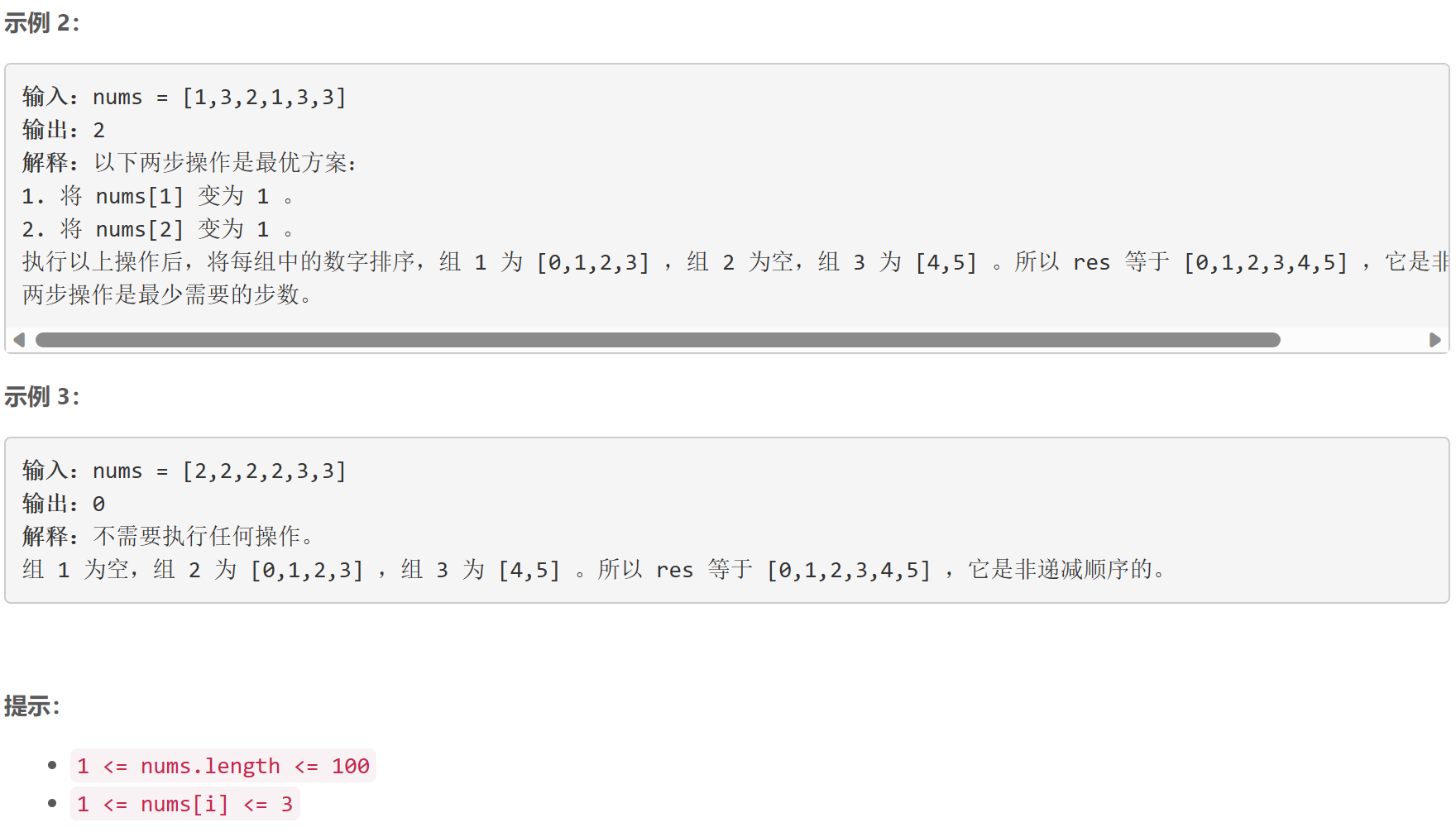
脑筋急转弯:设 n n n为数组长度,设原数组 n u m s nums nums上构建的新数组 r e s res res中最长上升子序列的长度为 l l l,则 n − l n-l n−l即为答案。数据范围小可以直接 O ( n 2 ) O(n^2) O(n2)动态规划求最长上升子序列,设 p [ i ] p[i] p[i]为以 r e s res res中以 r e s [ i ] res[i] res[i]结尾的最长上升子序列的长度,有状态转移方程: p [ i ] = m a x { 1 m a x { p [ j ] + 1 ∣ 0 ≤ j < i , r e s [ j ] < r e s [ i ] } p[i]=max\left\{\begin{matrix} 1 \\ max\{p[j]+1 \;|\; 0\le j<i,res[j]<res[i]\} \end{matrix}\right. p[i]=max{1max{p[j]+1∣0≤j<i,res[j]<res[i]}
class Solution {
public:
int minimumOperations(vector<int> &nums) {
int n = nums.size();
vector<int> li[4];
for (int i = 0; i < n; i++)
li[nums[i]].push_back(i);
vector<int> vec;//nums构建的res数组
for (int i = 1; i <= 3; i++)
if (!li[i].empty())
for (auto x: li[i])
vec.push_back(x);
int p[n];
for (int i = 0; i < n; i++) {
p[i] = 1;
for (int j = 0; j < i; j++)
if (vec[j] < vec[i])
p[i] = max(p[i], p[j] + 1);
}
return n - *max_element(p, p + n);
}
};
D 范围中美丽整数的数目
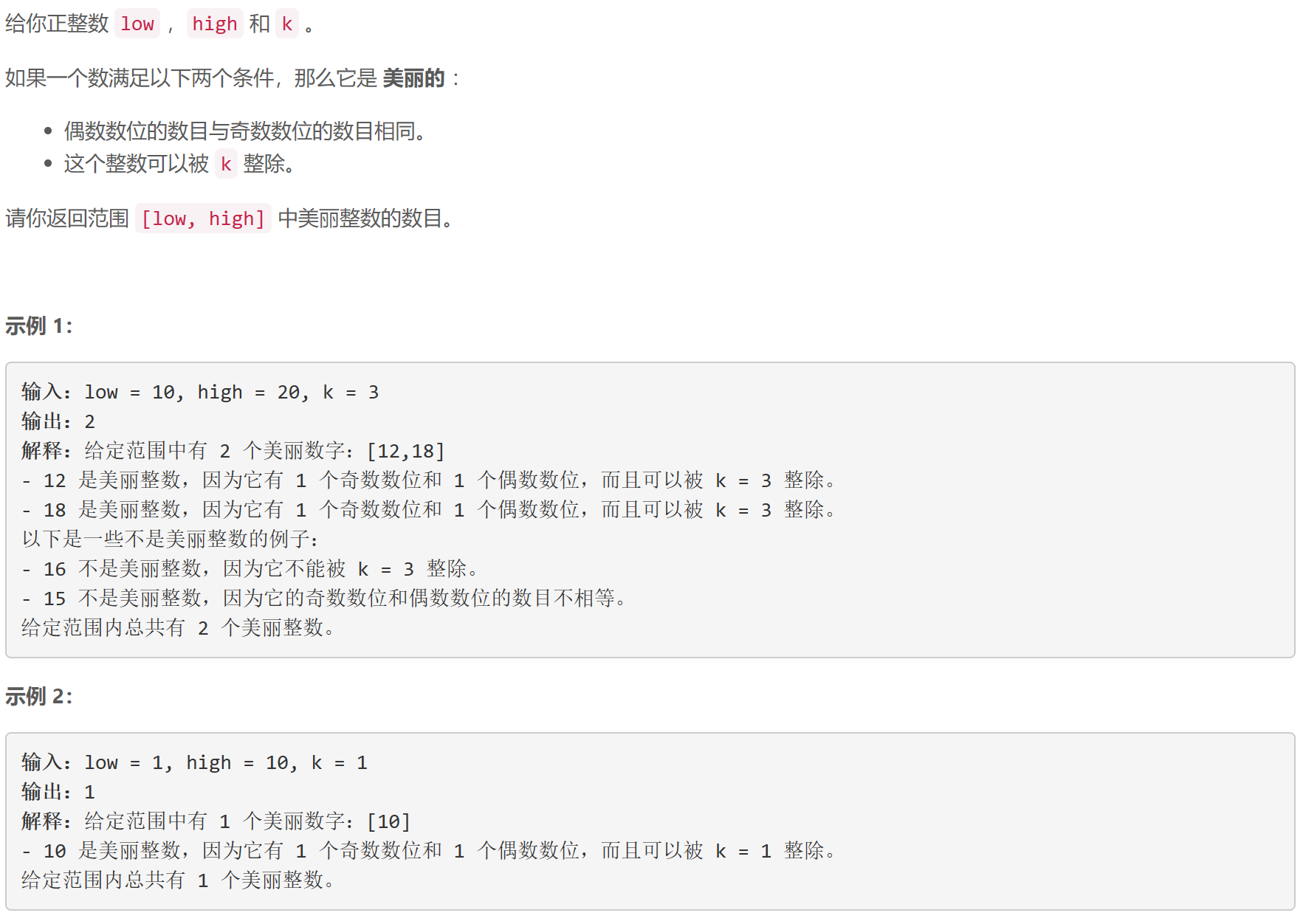
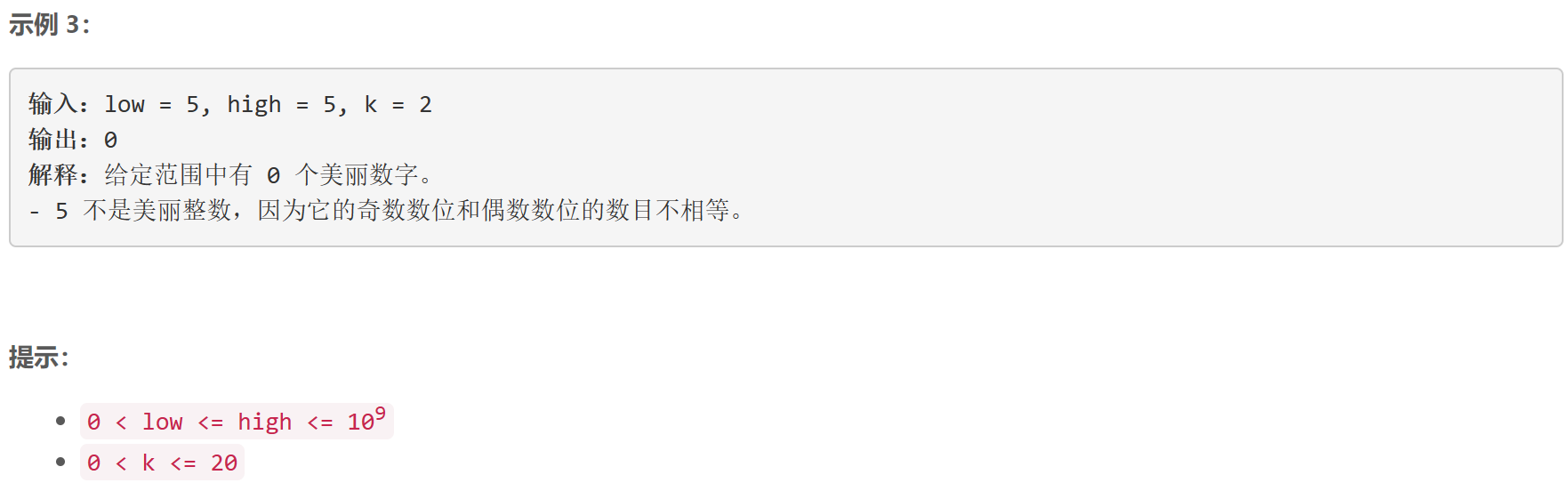
数位 d p dp dp:设 c o m p ( x , k ) comp(x, k) comp(x,k)为满足 0 ≤ i ≤ x 0\le i\le x 0≤i≤x的美丽的 i i i的个数,则原问题答案可表示为 c o m p ( h i g h , k ) − c o m p ( l o w − 1 , k ) comp(high,k)-comp(low-1,k) comp(high,k)−comp(low−1,k)。使用数位 d p dp dp求 c o m p ( x , k ) comp(x, k) comp(x,k):设 p [ l o c ] [ v a l ] [ e q ] [ o e ] [ m o d ] p[loc][val][eq][oe][mod] p[loc][val][eq][oe][mod]为满足 “当前数位下标为 l o c loc loc、当前数位之前是否有数字(有: v a l = 1 val=1 val=1,无: v a l = 0 val=0 val=0)、当前数位之前是否严格等于 x x x(是: e q = 1 eq=1 eq=1,否: e q = 0 eq=0 eq=0)、当前奇偶情况 o e oe oe(遇到奇数位+1,遇到偶数维-1),当前数位之前的数对 k k k取模的余数为 m o d mod mod ”的情况下的满足 0 ≤ i ≤ x 0\le i\le x 0≤i≤x的美丽的 i i i的个数,分类讨论实现状态转移。
class Solution {
public:
int comp(int x, int k) {
string s = to_string(x);
int n = s.size();
int p[n + 1][2][2][2 * n + 1][k];
memset(p, -1, sizeof(p));
int c = n;//oe维度需要的偏移量,防止下标出现负数
function<int(int, int, int, int, int)> get = [&](int loc, int val, int eq, int oe, int mod) {
if (p[loc][val][eq][oe][mod] != -1)
return p[loc][val][eq][oe][mod];
int &cur = p[loc][val][eq][oe][mod];
if (loc == n)//已遍历完所有数位
return cur = (val && oe == c && mod == 0) ? 1 : 0;
cur = 0;
if (!val) {//当前数位之前无数字
cur += get(loc + 1, 0, 0, oe, mod);//当前数位继续无数字
if (eq)//当前数位之前严格等于x
for (int i = 1; i <= s[loc] - '0'; i++)
cur += get(loc + 1, 1, i != s[loc] - '0' ? 0 : 1, oe + (i % 2 == 1 ? 1 : -1), (mod * 10 + i) % k);
else//当前数位之前不严格等于x
for (int i = 1; i <= 9; i++)
cur += get(loc + 1, 1, 0, oe + (i % 2 == 1 ? 1 : -1), (mod * 10 + i) % k);
} else {当前数位之前有数字
if (eq)//当前数位之前严格等于x
for (int i = 0; i <= s[loc] - '0'; i++)
cur += get(loc + 1, 1, i != s[loc] - '0' ? 0 : 1, oe + (i % 2 == 1 ? 1 : -1), (mod * 10 + i) % k);
else//当前数位之前不严格等于x
for (int i = 0; i <= 9; i++)
cur += get(loc + 1, 1, 0, oe + (i % 2 == 1 ? 1 : -1), (mod * 10 + i) % k);
}
return cur;
};
return get(0, 0, 1, c + 0, 0);
}
int numberOfBeautifulIntegers(int low, int high, int k) {
int a = comp(high, k), b = comp(low - 1, k);
return a - b;
}
};