【ICCV2023】Adaptive Frequency Filters As Efficient Global Token Mixers

news2024/11/16 5:25:22

Adaptive Frequency Filters As Efficient Global Token Mixers

论文：https://arxiv.org/abs/2307.14008

代码：暂未开源

解读：ICCV23｜轻量级视觉主干网络AFFNet：频域自适应频段过滤=空域全局动态大卷积核 - 知乎 (zhihu.com)

摘要

最近的vision transformer、大核CNN和MLP由于其在全局范围内的有效信息融合，在视觉任务中取得了显著的成功。然而，由于自注意机制、大内核或全连接层的高昂计算成本，它们的高效部署，特别是在移动设备上的高效部署仍然面临着值得注意的挑战。这项工作，将传统的卷积定理应用于深度学习，以解决这一问题，并揭示自适应频率滤波器可以作为有效的全局令牌混频器。

基于此，论文提出了自适应频率滤波（AFF）令牌混频器：Adaptive Frequency Filtering token mixer。通过傅里叶变换 (Fourier transform) 将特征变换到频域，并利用下面关系在数学上的等价：

在频域中 "通过逐位置的乘法操作过滤不同频段的特征"。
在空域中 "用一个动态卷积核执行特征混合操作，卷积核的大小为特征的大小"。

AFF令牌混合器作为主要的神经算子来构建一个轻量级的神经网络，称为AFFNet。

实验结果表明，与其他轻量级网络设计相比，AFFNet 在大多数视觉任务 (包括视觉识别和密集预测任务) 上实现了更好的精度和效率的权衡。

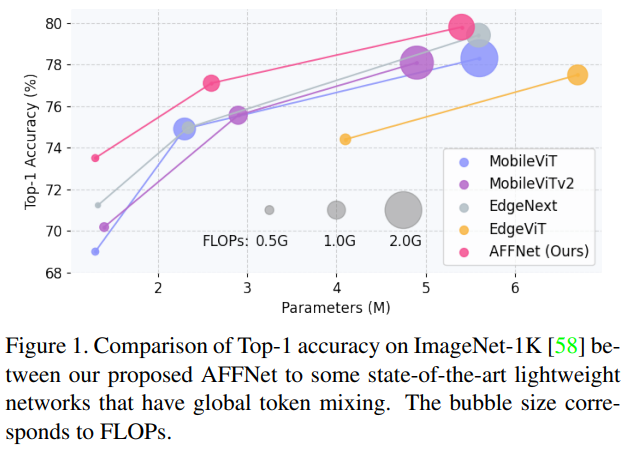
动机

AFFNet 设计了一种自适应频段过滤算子：Adaptive Frequency Filtering token mixer。

利用卷积定理，即：在一个域中的卷积在数学上等于其对应的傅里叶域中的 Hadamard 积 (也称为 Elementwise 乘积)。它的特点力求和 Self-Attention 对齐，包括：

全局信息建模 (Large Scope)：在频域中进行 Hadamard 积运算等价为在空域中进行大卷积核运算。
输入自适应 (Instance-Adaptive)：Self-Attention 的另一个性质是输入自适应，即计算出的 Attention 权重与输入图片的内容有关。动态卷积满足这一性质，但是同样存在计算代价高昂的问题，尤其是大核卷积的情况。直接加大卷积核很难直接满足这个需求。

方法

Token Mixing 过程表示

对于特征 $x^q$ , 经过 token mixing 后得到 $N(x^q)$ 的过程可以统一描述为下式:

对于 CNN 模型，如果使用大卷积核，卷积的计算复杂度随总的 token 数呈 $O(N^2)$ 的关系，对于 Transformer 模型，Self-Attention 的计算复杂度随总的 token 数也呈 $O(N^2)$ 的关系。MLP-Mixer 模型如果实现全局感受野需要大量的权重参数。因此自适应频段过滤算子希望借助频域设计高效，全局，以及输入自适应的算子。

自适应频段过滤算子的原理

卷积过程可表表达为：

AFFNet网络 & 自适应频段过滤算子

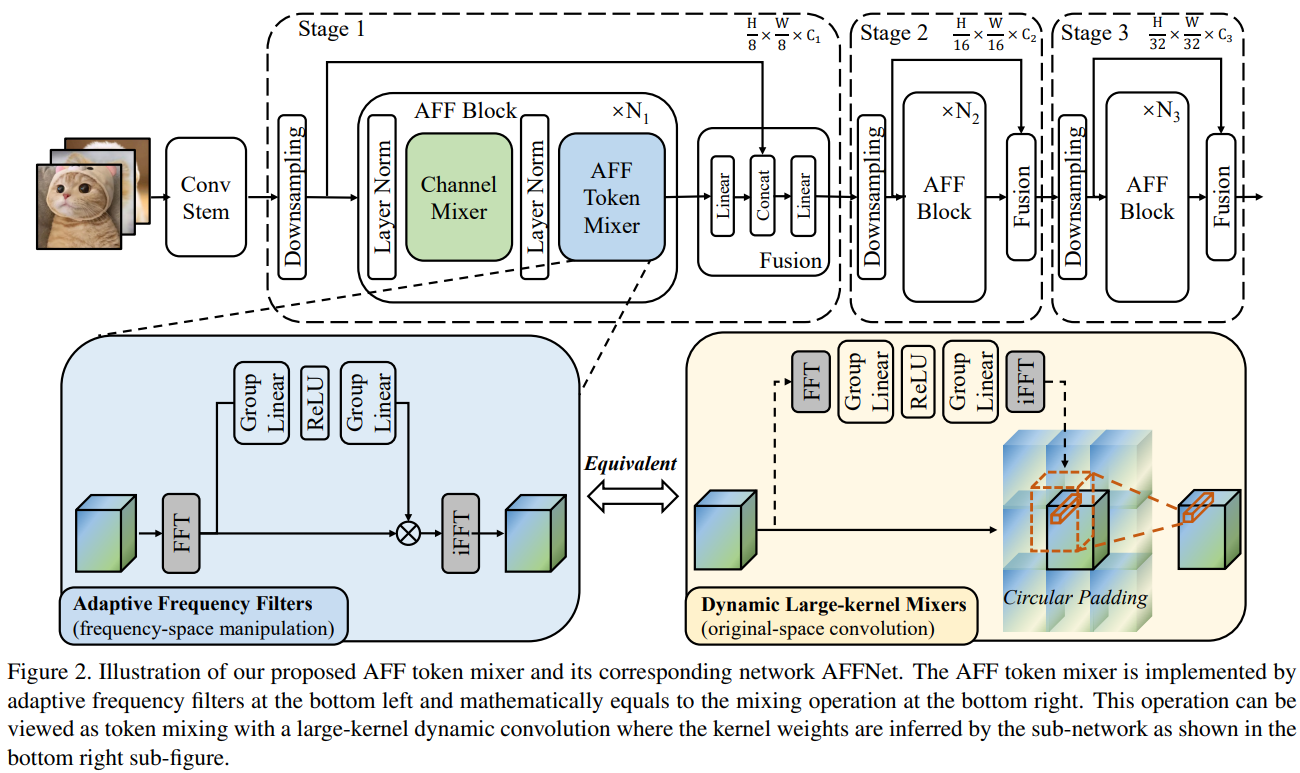
图2：自适应频段过滤算子，左侧：把空域特征转换到频域进行操作，右侧：直接在空域中进行动态卷积的操作相互等价

AFFNet 网络架构：每一层包括一个 MBConv 模块和一个自适应频段过滤算子。遵循 Transformer 架构的一般范式使用 Layer Normalization 归一化。整体架构可以写成下式：

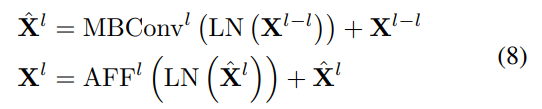
堆叠多个 AFF 块来构建轻量级骨干网络，即 AFFNet，AFFNet 使用惯例做法 Convolution Stem 来处理输入图片，每个 Stage 之间使用一个 Fusion 模块来融合特征。

自适应频段过滤算子流程：

1. 首先把输入特征做快速傅里叶变换 (Fast Fourier Transform， FFT) 转换到频域 $X_F=\mathcal{F}(X)$ , 其中 $\mathcal{F}(X)$ 为:

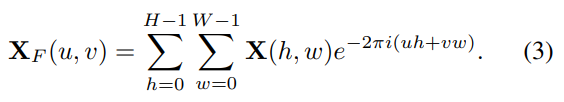
快速傅里叶变换的计算复杂度是 $O(NlogN)$ .

2. 通过可学习的频域滤波器 $\mathcal{M}(\mathcal{F}(X))$ 点乘输入的频域特征：

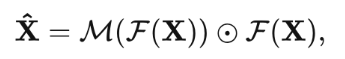
其中， $\mathcal{M}(\mathcal{F}(X))$ 是可学习的频域滤波器, 和频域特征有相同的形状。为了使网络尽可能轻量化, $\mathcal{M}(\cdot)$ 由 1×1 卷积层, 即线性层, ReLU 激活函数和一个线性层实现。

3. 通过快速傅里叶逆变换 (Inverse Fast Fourier Transform, IFFT) 转换回到空域：

至此， $\hat{X}$ 在数学上等价于采用大核动态卷积作为 Token Mixer 的权重得到的输出结果。

等价关系如下：

其中, $\mathcal{F}^{-1}[\mathcal{M}(\mathcal{F}(X))]$ 是与 X 形状相同的张量, 可以看作是大核动态卷积的卷积核 (满足性质 a : 全局信息建模), 这个 Kernel 与输入内容有关 (满足性质 b : 输入自适应)。因此, $\hat{X}$ 在数学上等价于采用大核动态卷积作为 Token Mixer 的权重得到的输出结果。根据傅里叶变换的性质, 对X 采用 circular padding。

自适应频段过滤算子使用极轻量级的网络构建一个可学习的频域滤波器 $\mathcal{M}(\cdot)$ , 然后计算 $\mathcal{M}(\cdot)$ 与频域特征之间的 Hadamard 积进行自适应频率滤波。最后再将特征通过傅里叶逆变换, 变换到空域。至此, 频域自适应频段过滤就相当于是空域全局动态大卷积核。

使用不同频率操作操作算子的比较：

实验

ImageNet-1K 图像识别

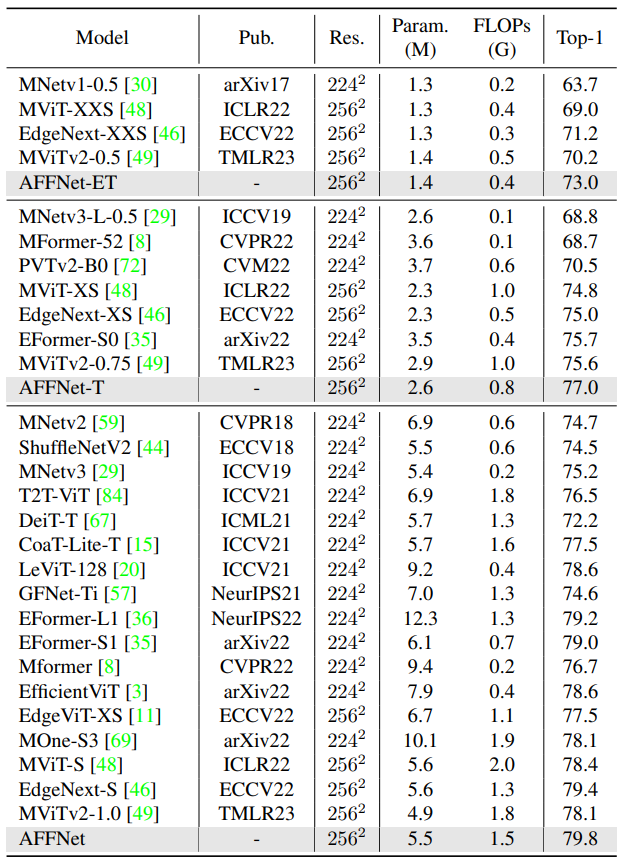
COCO 目标检测 & ADE20k 语义分割

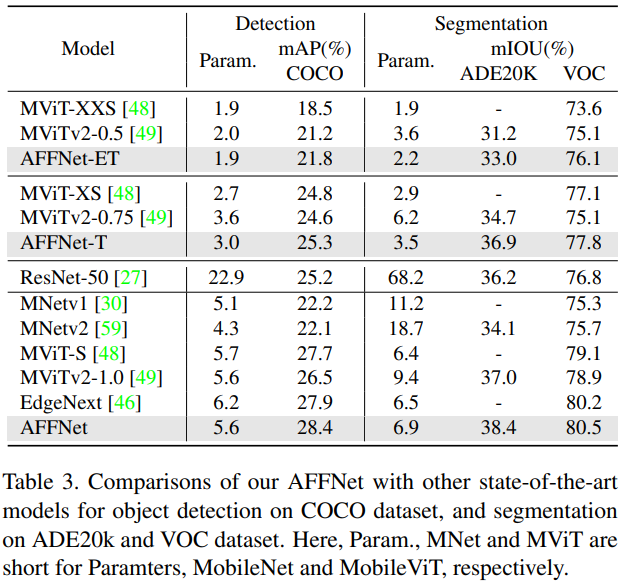
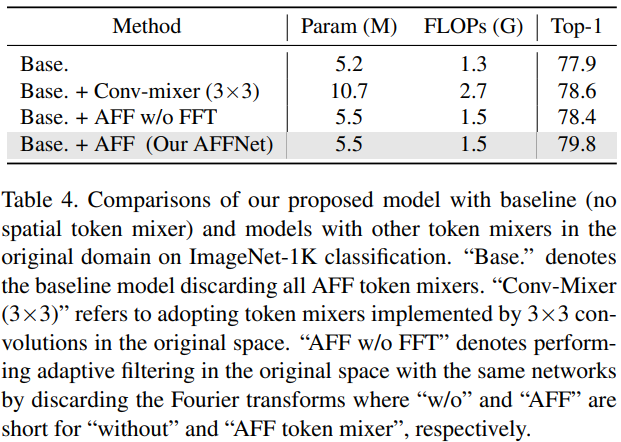
消融实验

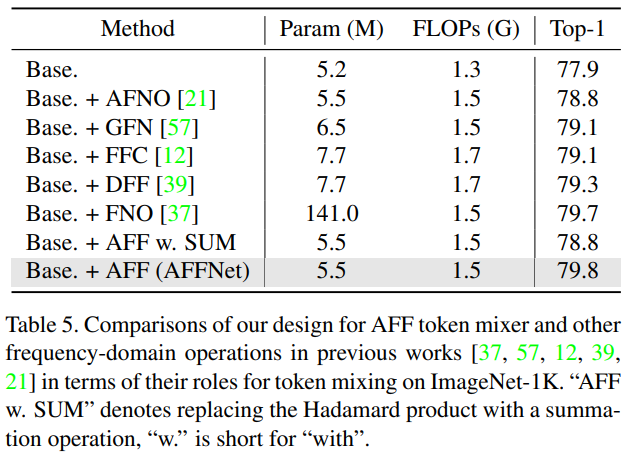
为了验证频域中混合信息的有效性，作者比较了在原始域和频域应用相同的自适应过滤操作，即进行了下面的实验：丢弃所有的傅里叶和傅里叶反变换，并保持其他与 AFFNet 相同，命名为 "Base.+AFF w/o FFT"。在相同的模型复杂度下，AFFNet 明显高出 1.4% 的 Top-1 精度。在原始域中应用自适应滤波甚至比仅仅用 Conv 作为 Token Mixer 弱 (取得了 78.6% 的 Top-1 精度，命名为 "Base.+Conv-mixer (3×3)")，这表明只有自适应频率滤波器可以作为有效的全局 Token Mixer.