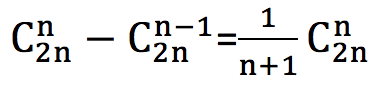定制化行业平板 在各行各业中的地位越来越重要，甚至在行业转型和发展中发挥着不可替代的作用。随着工业化社会的快速发展，工业生产对智控设备要求越来越高，运用的范畴也越来越普遍广泛，工业级平板就是其中一种应用广泛的设备。

新移科技专注于行业安卓平板定制开发，联发科 紫光展锐 高通安卓核心板 四核 / 八核方案、行业平板方案定制。
可选平台有：4G 模块：MT6761、MT6762、MT6765、MT8788、MT6785、MT6739 、T618、T610、T310等；5G 模块：MT6853、MT6833、MT6877、T820等。

新移科技行业平板方案成熟，支持智能终端软件以及 PCBA 硬件差异化定制，现以 MT8788 平台为例介绍详情。

 

 

联发科MT8788安卓核心板平台介绍
MTK8788设备具有集成的蓝牙、fm、wlan和gps模块，是一个高度集成的基带平台，包括调制解调器和应用处理子系统，启用LTE/LTE-A和C2K智能设备应用程序。该芯片集成了工作在2.0GHz的ARM Cortex-A73、最高可达2.0GHz的ARM Cortex-A53和功能强大的多标准视频编解码器。此外，一个广泛的接口和连接外围设备包括接口到相机，触摸屏显示器和ufs/mmc/sd卡。
 

联发科MT8788芯片参数：
四芯ARM Cortex-A73 MPCoreTM在2.0GHz工作
四芯ARM Cortex-A53 MPCoreTM在2.0GHz工作
LPDDR3可达4GB(32位数据总线宽度的单通道)
LPDR4x最高可达8GB（双通道，具有16位数据总线宽度）
内存时钟到LPDDR3-1866或LPDDR4-3600
LTE Cat 7(300Mbps)
包括WLAN/BT/FM/GPS在内的嵌入式连接系统
支持FHD+(2400x1080)
OpenGL ES 3.0三维图形加速器
ISP支持25mp@30fps
HEVC 1080p@30fps译码器
H.264 1080p@30fps编码器
语音编解码器(FR，HR，EFR，AMR FR，AMR HR和宽带AMR)
 

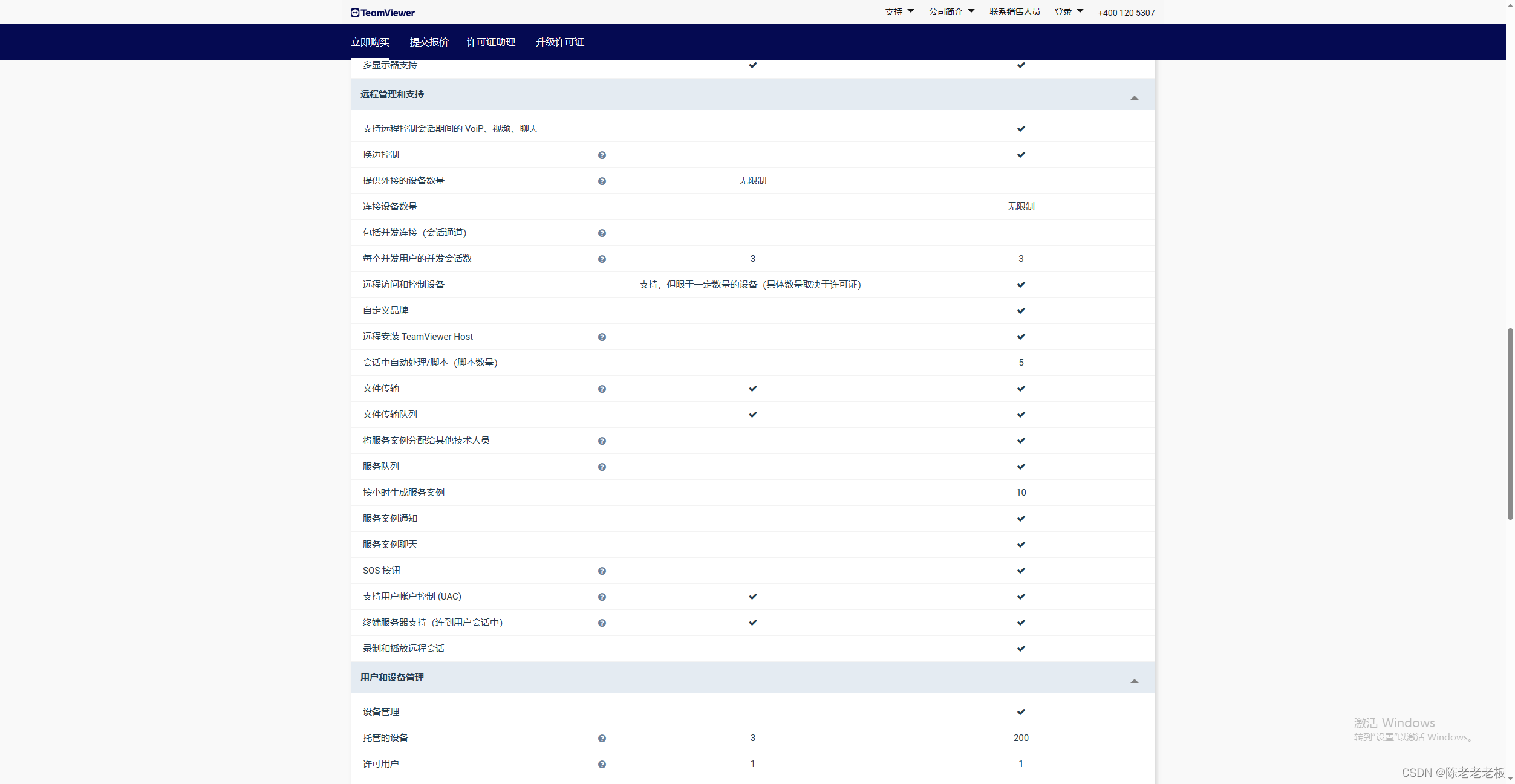
基于MTK8788安卓核心板行业定制平板产品参数：

 

 

---

更多资料技术了解，可到 · 新移科技技术论坛 - Powered by Discuz!