一、简介

首先，随机选择K个对象，而且所选择的每个对象都代表一个组的初始均值或初始的组中心值，对剩余的每个对象，根据其与各个组初始均值的距离，将他们分配各最近的（最相似）小组，然后重新计算每个小组新的均值，这个过程不断重复，直到所有的对象在K组分布中都找到离自己最近的组。

 

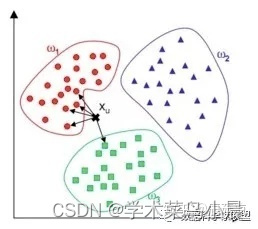
算法流程：

    计算已知类别数据集中的点与当前点之间的距离
    按照距离值进行排序
    选取最小的k个距离，并统计这k个点所在类别出现的概率
    返回前k个点出现频率最高的类别作为当前点的预测分类

求解方法：距离公式

 

二、距离度量选择

 欧式距离：

d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} d=(x1​−x2​)2+(y1​−y2​)2

 

标准化欧氏距离，余弦距离，汉明距离，杰卡德距离：

杰卡德相似系数：两个集合A和B的交集元素在A、B的并集中所占的比例
杰卡德距离：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的

马氏距离：

用来表示数据的协方差距离（或两个分布的距离），是一种有效的计算两个位置样本集的相似度的方法，考虑到各种特性之间的联系，独立于测量尺度。

三、K值的选择

如果选择较小的K值，就相当于用较小的邻域中的训练实例进行预测，“学习”的近似误差会减小，只有输入实例较近的训练实例才会对预测结果起作用。但缺点是“学习”的估计误差会增大，预测结果会对近邻实例点非常敏感。如果邻近的实例点恰巧是噪声，预测就会出错。换句话说，K值得减小就意味着整体模型非常复杂，容易发生过拟合。

如果选择较大的K值，就相当于用较大邻域中的训练实例进行预测，其实优点是减少学习的估计误差，但缺点是学习的近似误差会增大。这时与输入实例较远的训练实例也会起预测作用，使预测发生错误，k值的增大就意味着整体的模型变得简单，容易发生欠拟合。可以假定极端条件K=N，那么无论输入实例是什么，都将简单的预测它属于训练实例中最多的类。这时，模型过于简单，完全忽略训练中的大量有用信息，是不可取的。

在应用中，通常采用交叉验证法来选择最优K值。从上面的分析也可以知道，一般K值取得比较小。我们会选取K值在较小的范围，同时在验证集上准确率最高的那一个确定为最终的算法超参数K。

四、knn优缺点

优点：

1）算法简单，理论成熟，既可以用来做分类也可以用来做回归。

2）可用于非线性分类。

3）没有明显的训练过程，而是在程序开始运行时，把数据集加载到内存后，不需要进行训练，直接进行预测，所以训练时间复杂度为0。

4）由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属的类别，因此对于类域的交叉或重叠较多的待分类样本集来说，KNN方法较其他方法更为适合。

5）该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量比较小的类域采用这种算法比较容易产生误分类情况。

缺点：

1）需要算每个测试点与训练集的距离，当训练集较大时，计算量相当大，时间复杂度高，特别是特征数量比较大的时候。

2）需要大量的内存，空间复杂度高。

3）样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少），对稀有类别的预测准确度低。

4）是lazy learning方法，基本上不学习，导致预测时速度比起逻辑回归之类的算法慢。

五、总结

KNN是一个特别容易理解的模型，因此，当需要一个特别容易解释的模型的时候，比如需要向用户解释原因的推荐算法，我们可以使用KNN。例如，我们可以使用knn算法做到比较通用的现有用户产品推荐，基于用户的最近邻（长得最像的用户）买了什么产品来推荐，是一种基于电子商务和sns的精确营销，只需要定期维护更新最近邻表就可以，基于最近邻表做搜索可以很实时。