链接：

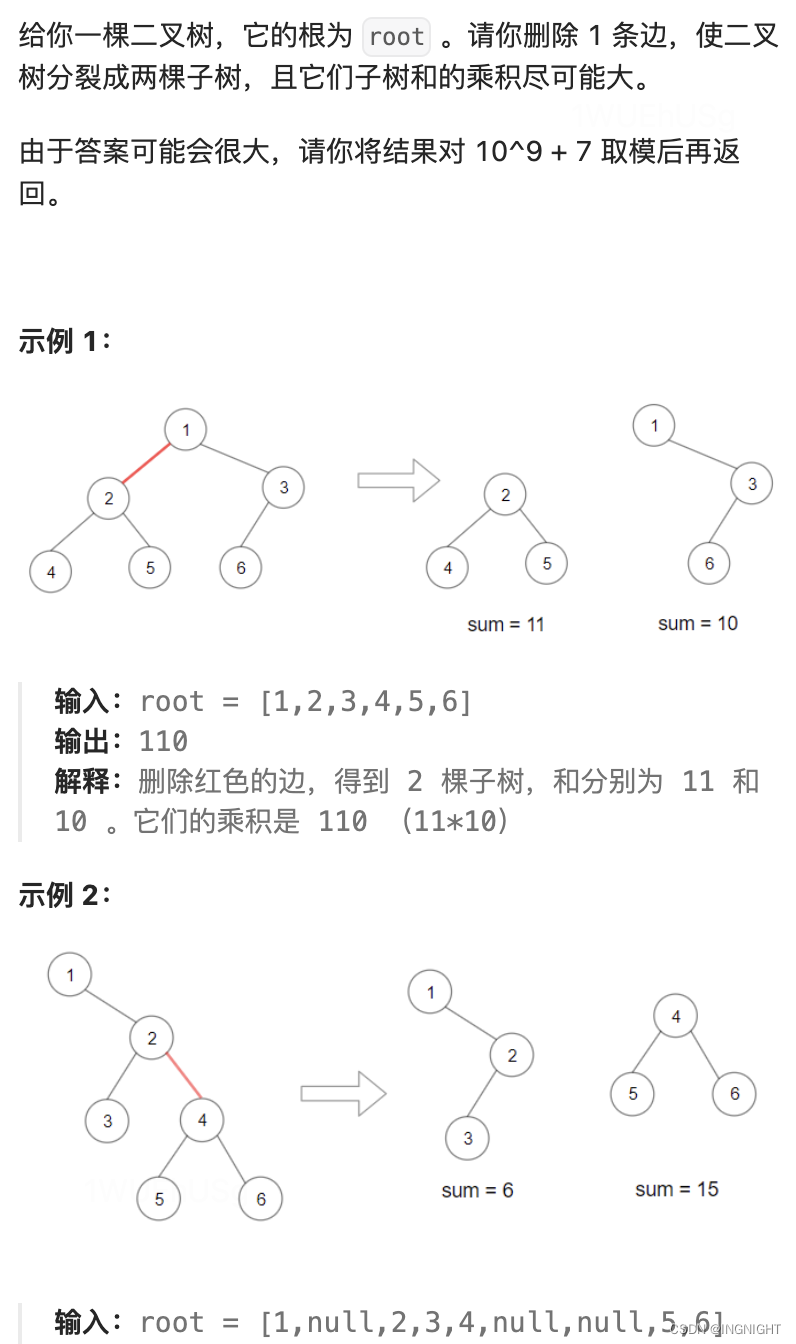
​​​​​​1339. 分裂二叉树的最大乘积

题解：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxProduct(TreeNode* root) {
        if (!root) {
            return 0;
        }
        int sum = 0;
        dfs(root, sum);
        long long result = 0;
        dfs2(root, sum, result);        
        int mod = 1000000007;
        return result%mod;
    }
private:
    void dfs(TreeNode* root, int& sum) {
        if (!root) {
            return;
        }
        sum += root->val;
        dfs(root->left, sum);
        dfs(root->right, sum);
    }
    int dfs2(TreeNode* root, int sum, long long& result) {
        if (!root) {
            return 0;
        }
        long long cur = dfs2(root->left, sum, result) + dfs2(root->right, sum, result) + root->val;
        long long tmp_result = (sum-cur)*cur;
        if (tmp_result > result) {
            result = tmp_result;
        }
        return cur;
    }
};