选择排序的思想是：双重循环遍历数组，每经过一轮比较，找到最小元素的下标，将其交换至首位。

public static void selectionSort(int[] arr) {
    int minIndex;
    for (int i = 0; i < arr.length - 1; i++) {
        minIndex = i;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[minIndex] > arr[j]) {
                // 记录最小值的下标
                minIndex = j;
            }
        }
        // 将最小元素交换至首位
        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
}

        选择排序就好比第一个数字站在擂台上，大吼一声：“还有谁比我小？”。剩余数字来挨个打擂，如果出现比第一个数字小的数，则新的擂主产生。每轮打擂结束都会找出一个最小的数，将其交换至首位。经过 n-1 轮打擂，所有的数字就按照从小到大排序完成了。

        现在让我们思考一下，冒泡排序和选择排序有什么异同？

相同点：

• 都是两层循环，时间复杂度都为  Ｏ(n²)；
• 都只使用有限个变量，空间复杂度  Ｏ(1)；

不同点：

• 冒泡排序在比较过程中就不断交换；而选择排序增加了一个变量保存最小值 / 最大值的下标，遍历完成后才交换，减少了交换次数。

事实上，冒泡排序和选择排序还有一个非常重要的不同点，那就是：

• 冒泡排序法是稳定的，选择排序法是不稳定的。

想要理解这点不同，我们先要知道什么是排序算法的稳定性。

排序算法的稳定性

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i] = r[j]，且 r[i] 在 r[j] 之前，而在排序后的序列中，r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。

        理解了稳定性的定义后，我们就能分析出：冒泡排序中，只有左边的数字大于右边的数字时才会发生交换，相等的数字之间不会发生交换，所以它是稳定的。

        而选择排序中，最小值和首位交换的过程可能会破坏稳定性。比如数列：[2, 2, 1]，在选择排序中第一次进行交换时，原数列中的两个 2 的相对顺序就被改变了，因此，我们说选择排序是不稳定的。

        那么排序算法的稳定性有什么意义呢？其实它只在一种情况下有意义：当要排序的内容是一个对象的多个属性，且其原本的顺序存在意义时，如果我们需要在二次排序后保持原有排序的意义，就需要使用到稳定性的算法。

        举个例子，如果我们要对一组商品排序，商品存在两个属性：价格和销量。当我们按照价格从高到低排序后，要再按照销量对其排序，这时，如果要保证销量相同的商品仍保持价格从高到低的顺序，就必须使用稳定性算法。

        当然，算法的稳定性与具体的实现有关。在修改比较的条件后，稳定性排序算法可能会变成不稳定的。如冒泡算法中，如果将「左边的数大于右边的数，则交换」这个条件修改为「左边的数大于或等于右边的数，则交换」，冒泡算法就变得不稳定了。

        同样地，不稳定排序算法也可以经过修改，达到稳定的效果。思考一下，选择排序算法如何实现稳定排序呢？

        实现的方式有很多种，这里给出一种最简单的思路：新开一个数组，将每轮找出的最小值依次添加到新数组中，选择排序算法就变成稳定的了。

        但如果将寻找最小值的比较条件由arr[minIndex] > arr[j]修改为arr[minIndex] >= arr[j]，即使新开一个数组，选择排序算法依旧是不稳定的。所以分析算法的稳定性时，需要结合具体的实现逻辑才能得出结论，我们通常所说的算法稳定性是基于一般实现而言的。

二元选择排序

        选择排序算法也是可以优化的，既然每轮遍历时找出了最小值，何不把最大值也顺便找出来呢？这就是二元选择排序的思想。

        使用二元选择排序，每轮选择时记录最小值和最大值，可以把数组需要遍历的范围缩小一倍。

public static void selectionSort2(int[] arr) {
    int minIndex, maxIndex;
    // i 只需要遍历一半
    for (int i = 0; i < arr.length / 2; i++) {
        minIndex = i;
        maxIndex = i;
        for (int j = i + 1; j < arr.length - i; j++) {
            if (arr[minIndex] > arr[j]) {
                // 记录最小值的下标
                minIndex = j;
            }
            if (arr[maxIndex] < arr[j]) {
                // 记录最大值的下标
                maxIndex = j;
            }
        }
        // 如果 minIndex 和 maxIndex 都相等，那么他们必定都等于 i，且后面的所有数字都与 arr[i] 相等，此时已经排序完成
        if (minIndex == maxIndex) break;
        // 将最小元素交换至首位
        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
        // 如果最大值的下标刚好是 i，由于 arr[i] 和 arr[minIndex] 已经交换了，所以这里要更新 maxIndex 的值。
        if (maxIndex == i) maxIndex = minIndex;
        // 将最大元素交换至末尾
        int lastIndex = arr.length - 1 - i;
        temp = arr[lastIndex];
        arr[lastIndex] = arr[maxIndex];
        arr[maxIndex] = temp;
    }
}

        我们使用 minIndex 记录最小值的下标，maxIndex 记录最大值的下标。每次遍历后，将最小值交换到首位，最大值交换到末尾，就完成了排序。

        由于每一轮遍历可以排好两个数字，所以最外层的遍历只需遍历一半即可。

        二元选择排序中有一句很重要的代码，它位于交换最小值和交换最大值的代码中间：

if (maxIndex == i) maxIndex = minIndex;

        这行代码的作用处理了一种特殊情况：如果最大值的下标等于 i，也就是说 arr[i] 就是最大值，由于 arr[i] 是当前遍历轮次的首位，它已经和 arr[minIndex] 交换了，所以最大值的下标需要跟踪到 arr[i] 最新的下标 minIndex。

二元选择排序的效率

        在二元选择排序算法中，数组需要遍历的范围缩小了一倍。那么这样可以使选择排序的效率提升一倍吗？

        从代码可以看出，虽然二元选择排序最外层的遍历范围缩小了，但 for 循环内做的事情翻了一倍。也就是说二元选择排序无法将选择排序的效率提升一倍。但实测会发现二元选择排序的速度确实比选择排序的速度快一点点，它的速度提升主要是因为两点：

• 在选择排序的外层 for 循环中，i 需要加到 arr.length - 1 ，二元选择排序中 i 只需要加到 arr.length / 2；
• 在选择排序的内层 for 循环中，j 需要加到 arr.length ，二元选择排序中 j 只需要加到 arr.length - i；

我们不妨发扬一下极客精神，一起来做一个统计实验：

public class TestSelectionSort {
    public static void selectionSort(int[] arr) {
        int countI = 0;
        int countJ = 0;
        int countArr = 0;
        int minIndex;
        countI++;
        for (int i = 0; i < arr.length - 1; i++, countI++) {
            minIndex = i;
            countJ++;
            for (int j = i + 1; j < arr.length; j++, countJ++) {
                if (arr[minIndex] > arr[j]) {
                    // 记录最小值的下标
                    minIndex = j;
                }
                countArr++;
            }
            // 将最小元素交换至首位
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
        int count = countI + countJ + countArr;
        System.out.println("selectionSort: countI = " + countI + ", countJ = " + countJ + ", countArr = " + countArr + ", count = " + count);
    }

    public static void selectionSort2(int[] arr) {
        int countI = 0;
        int countJ = 0;
        int countArr = 0;
        int minIndex, maxIndex;
        countI++;
        // i 只需要遍历一半
        for (int i = 0; i < arr.length / 2; i++, countI++) {
            minIndex = i;
            maxIndex = i;
            countJ++;
            for (int j = i + 1; j < arr.length - i; j++, countJ++) {
                if (arr[minIndex] > arr[j]) {
                    // 记录最小值的下标
                    minIndex = j;
                }
                if (arr[maxIndex] < arr[j]) {
                    // 记录最大值的下标
                    maxIndex = j;
                }
                countArr += 2;
            }
            // 如果 minIndex 和 maxIndex 都相等，那么他们必定都等于 i，且后面的所有数字都与 arr[i] 相等，此时已经排序完成
            if (minIndex == maxIndex) break;
            // 将最小元素交换至首位
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
            // 如果最大值的下标刚好是 i，由于 arr[i] 和 arr[minIndex] 已经交换了，所以这里要更新 maxIndex 的值。
            if (maxIndex == i) maxIndex = minIndex;
            // 将最大元素交换至末尾
            int lastIndex = arr.length - 1 - i;
            temp = arr[lastIndex];
            arr[lastIndex] = arr[maxIndex];
            arr[maxIndex] = temp;
        }
        int count = countI + countJ + countArr;
        System.out.println("selectionSort2: countI = " + countI + ", countJ = " + countJ + ", countArr = " + countArr + ", count = " + count);
    }
}

        在这个类中，我们用 countI 记录 i 的比较次数，countJ 记录 j 的比较次数，countArr 记录 arr 的比较次数，count 记录总比较次数。

测试用例：

import org.junit.Test;

import java.util.ArrayList;

public class UnitTest {
    @Test
    public void test() {
        ArrayList<Integer> list = new ArrayList<>();
        for (int i = 0; i <= 1000; i++) {
            // ArrayList 转 int[]
            int[] arr = list.stream().mapToInt(Integer::intValue).toArray();
            System.out.println("*** arr.length = " + arr.length + " ***");
            TestSelectionSort.selectionSort(arr);
            TestSelectionSort.selectionSort2(arr);
            list.add(i);
        }
    }
}

这里列出部分测试结果：

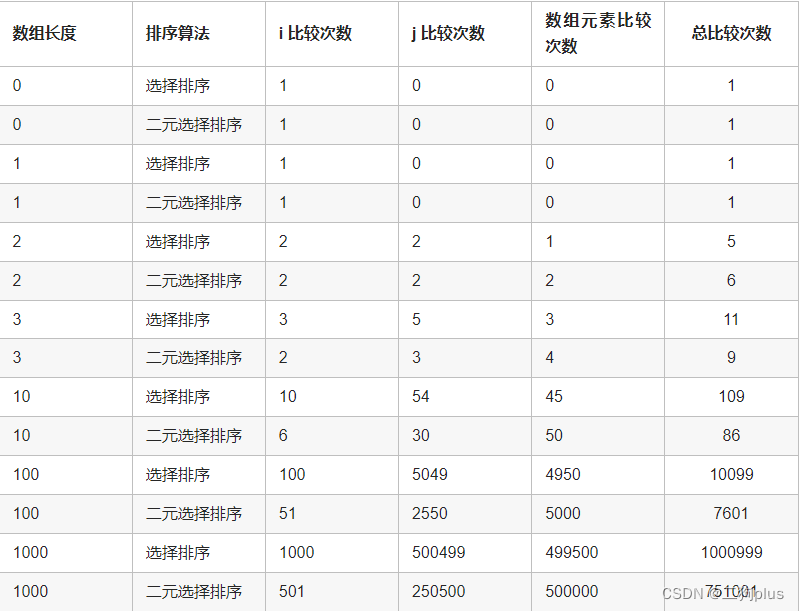
        可以看到，二元选择排序中， arr 数组的比较次数甚至略高于选择排序的比较次数，整体是相差无几的。只是 i 和 j 的比较次数较少，正是在这两个地方提高了效率。

        并且，在二元选择排序中，我们可以做一个剪枝优化，当 minIndex == maxIndex 时，说明后续所有的元素都相等，就好比班上最高的学生和最矮的学生一样高，说明整个班上的人身高都相同了。此时已经排序完成，可以提前跳出循环。通过这个剪枝优化，对于相同元素较多的数组，二元选择排序的效率将远远超过选择排序。

和选择排序一样，二元选择排序也是不稳定的。