特勒根定理、互易定理、对偶定理比较难,非常重要,因为他们可以解决其他定理无法解决的问题。
1、特勒根定理1——个人感觉像能量守恒
特勒根定理与基尔霍夫定理齐名,与拓扑结构有关。都适用于任何线性非线性,时变的非时变的元件的集总电路。

注意:
1)支路吸收,如果支路算出来吸收功率大于零,则实际是吸收功率,如果实际支路算出来小于零,则实际是发出功率。
2)集总参数电路在P1中讲了
2、用基尔霍夫电流定理证明特勒根定理1
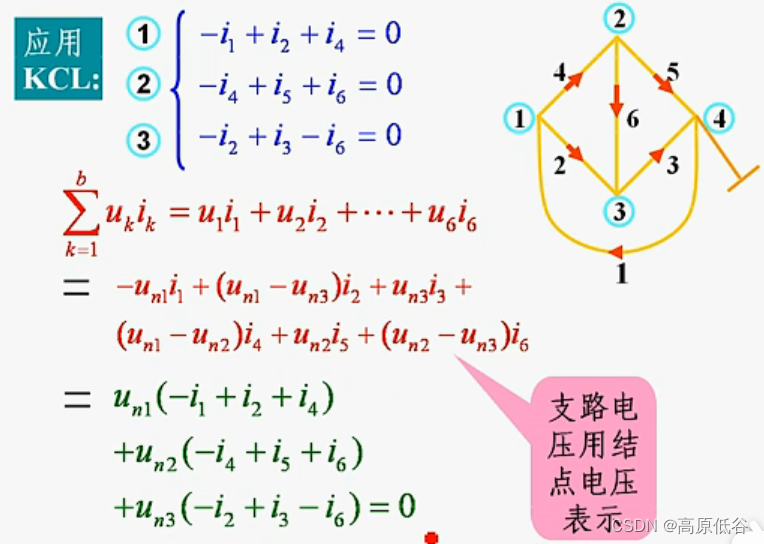
3、特勒根定理2—可以发现就不像能量守恒了
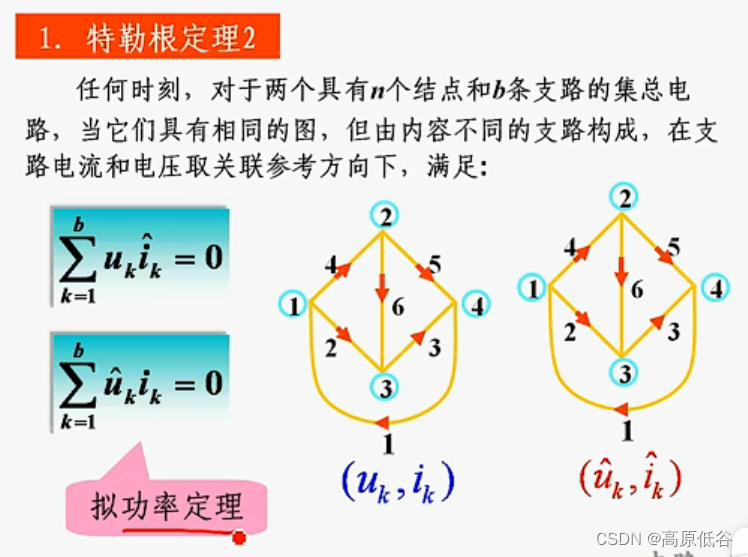
4、用基尔霍夫电流定理证明特勒根定理2

5、实际使用
特勒根定理2可以把两个图联系到一起。
黑箱结构有时候只能用特勒根定理2求解。
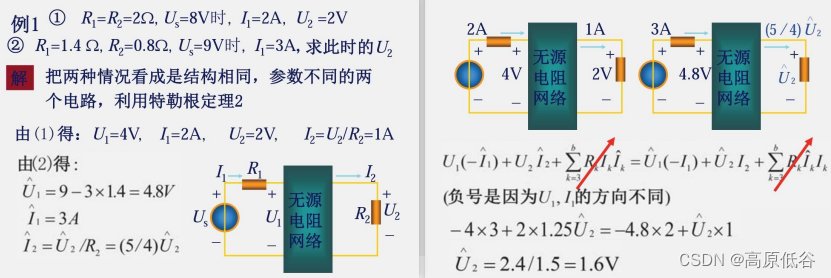


6、互易定理


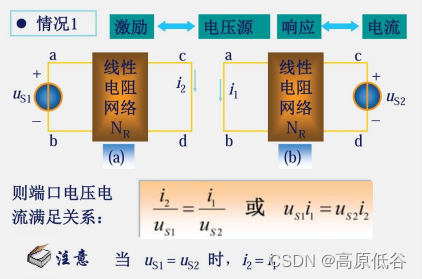
上图中关系式是应用特勒根定理2联系两个电路图得到的。

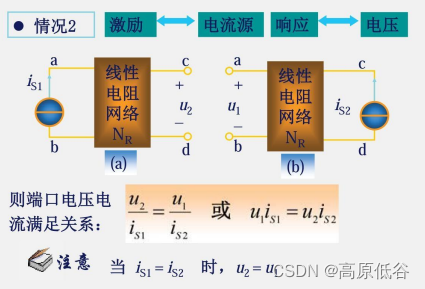
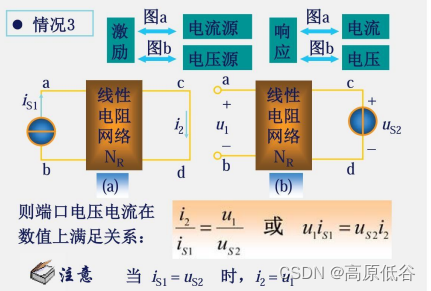

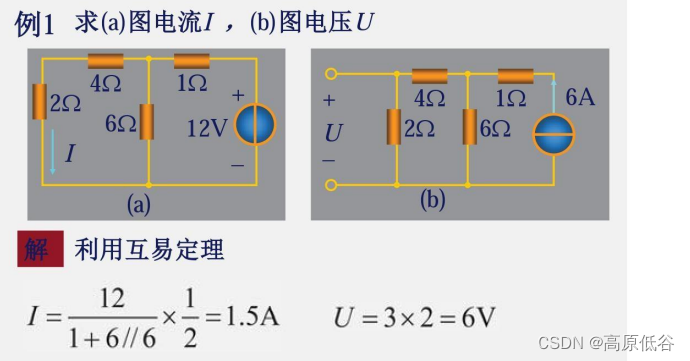
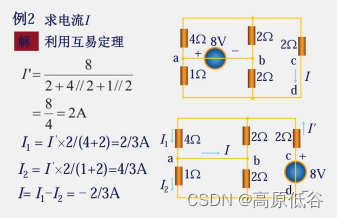
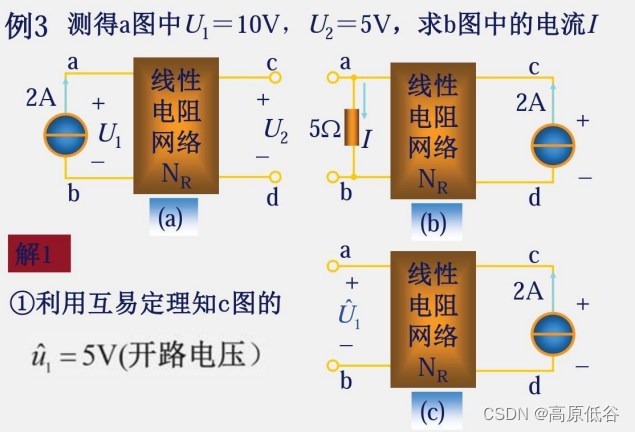
图a是2A电流源激励,5v的响应。图c将电流源激励从图a的左边到右边。根据互易定理得:图c还是2A电流源激励,5v的响应。
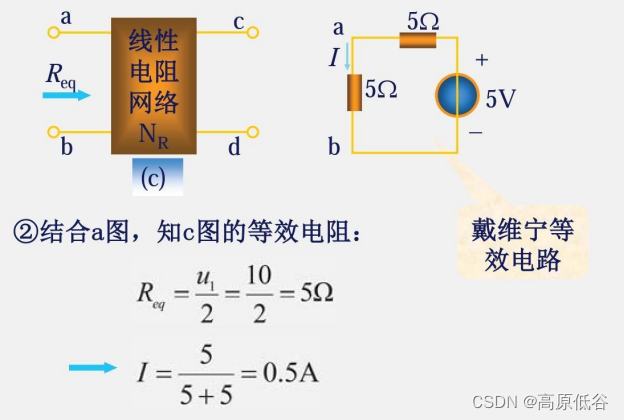
易错点:认为在图中NR的等效电阻与a,b两端间电阻一定是并联关系。可能只是与NR的部分网络并联。
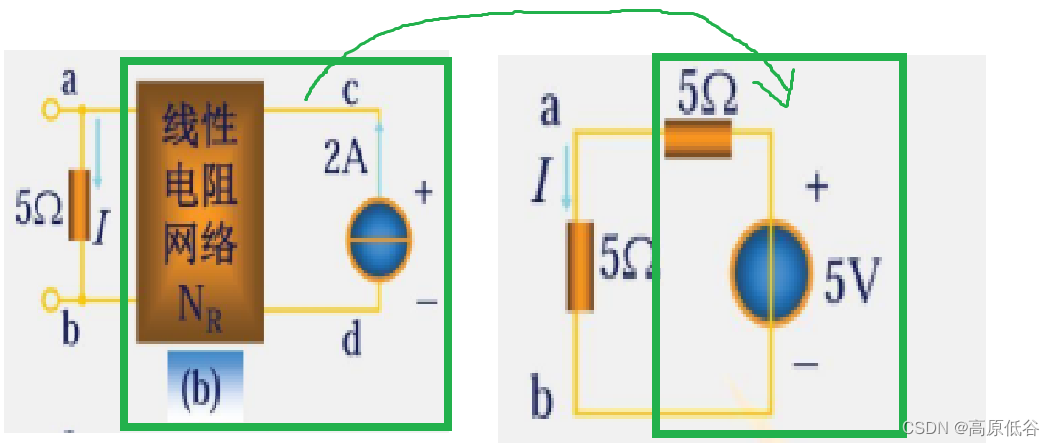
互易定理来源于特勒根定理,互易定理可以解决,特勒根定理也肯定可以解决。
下图的公式是选取参考方向后,省略黑箱部分公式后列出的:
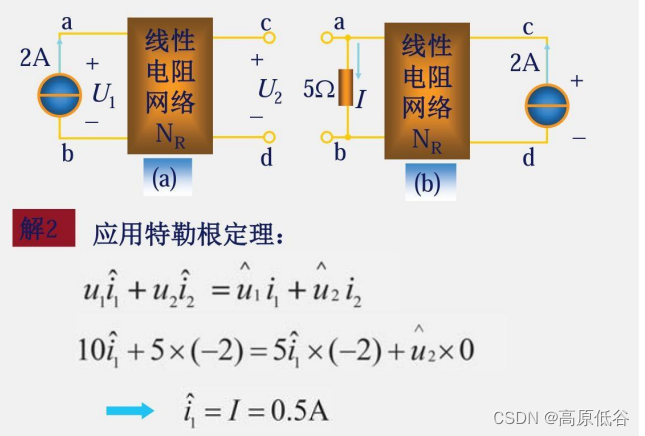
多个受控源的控制系数满足什么条件是互易等式成立。

所以电路只有一个受控源,则一定不具互易性。
存在多个受控源,则不一定具有互易性。可能存在彼此配合恰巧满足互易。
7、定理的综合应用
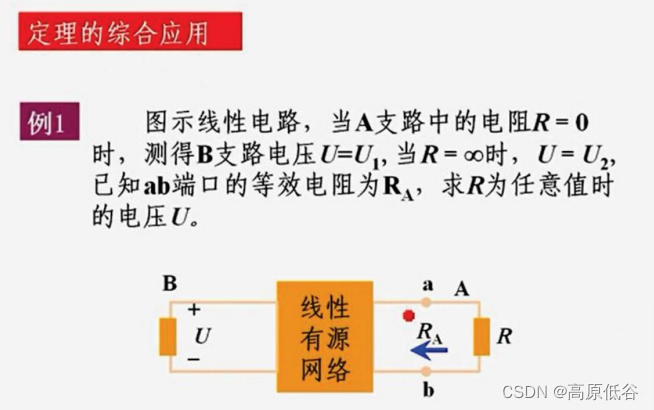
显然这是一个隐式的例子,没有具体连接结构,显然要用精彩绝伦的特勒根定理1、2,互易定理、对偶定理。
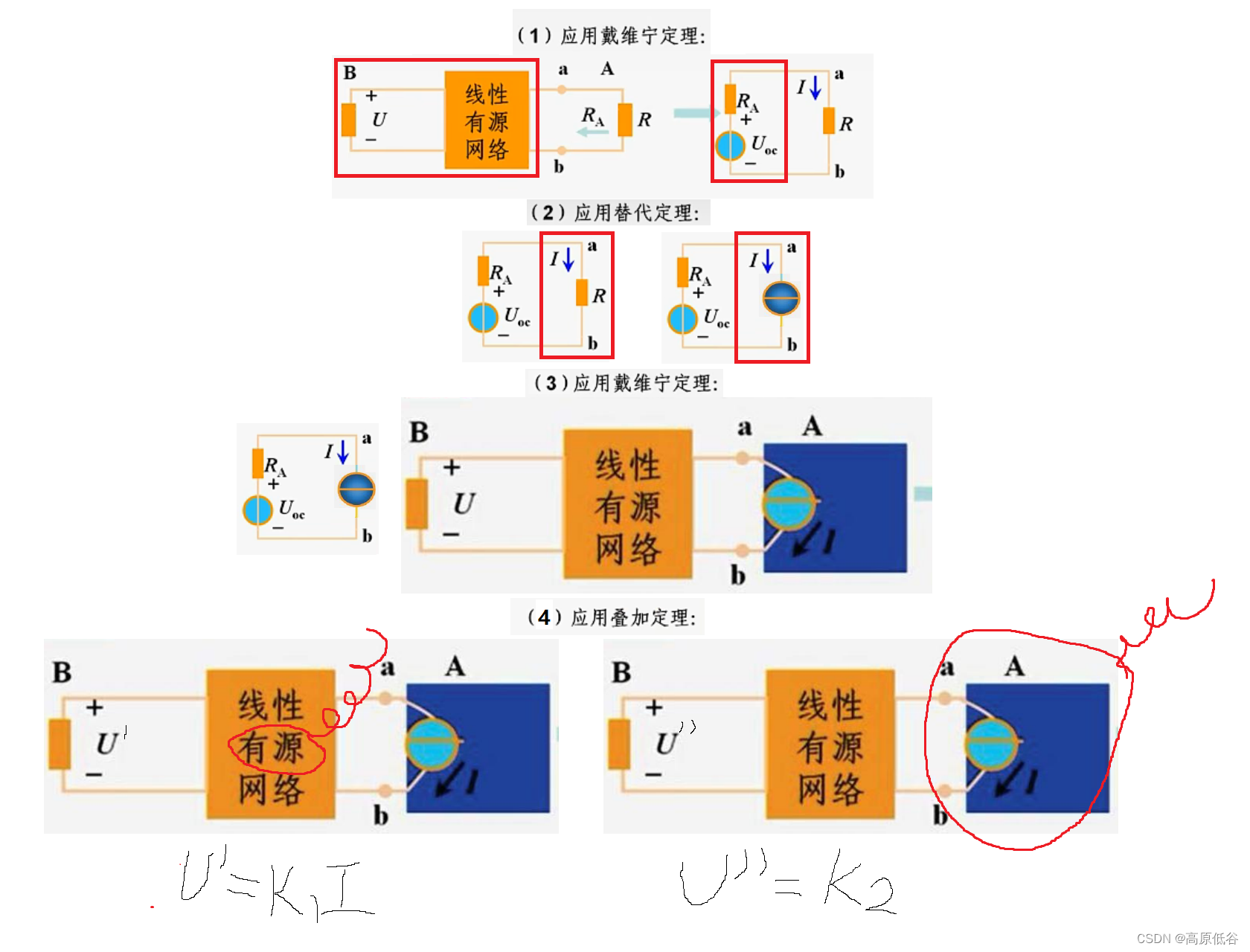
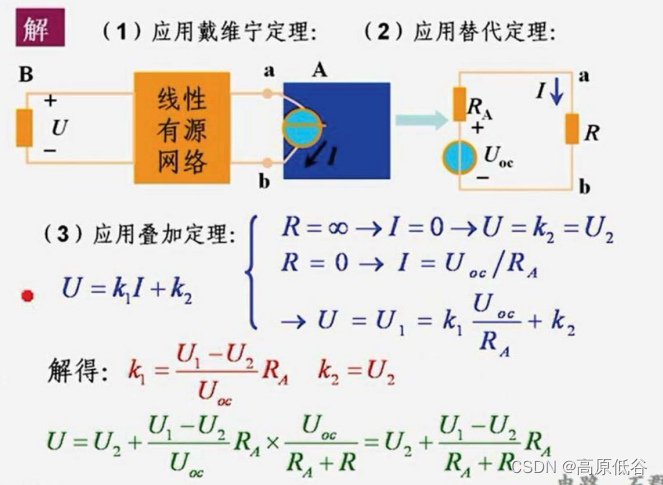
下面这题水平也高:
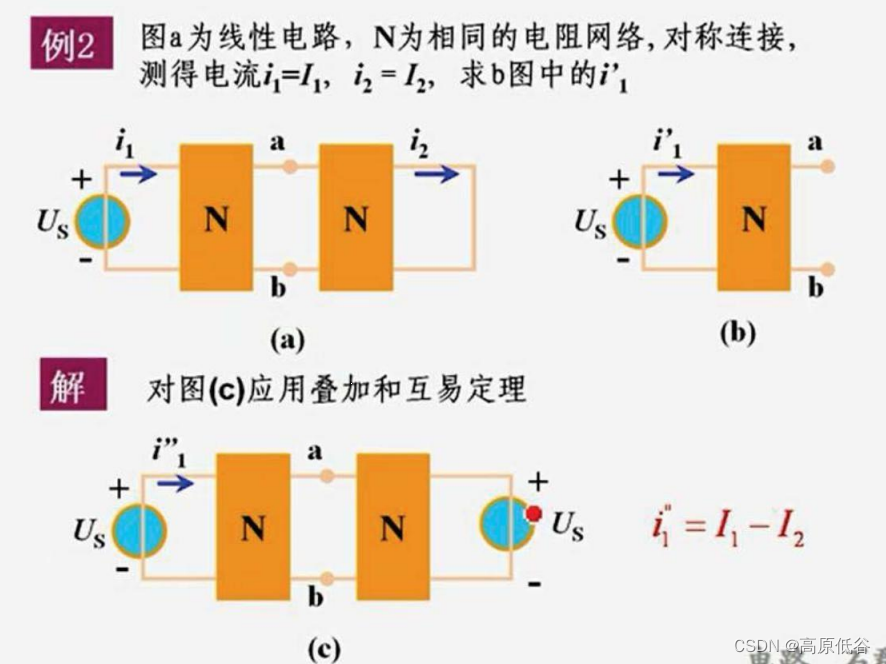
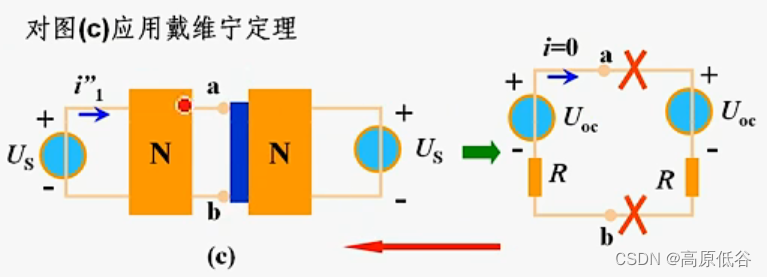
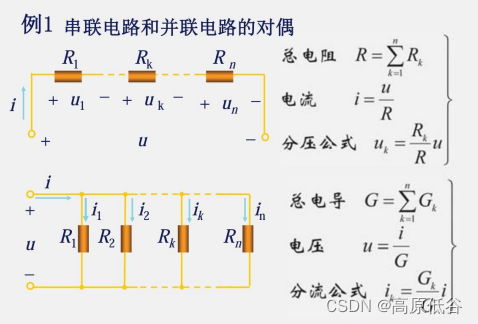
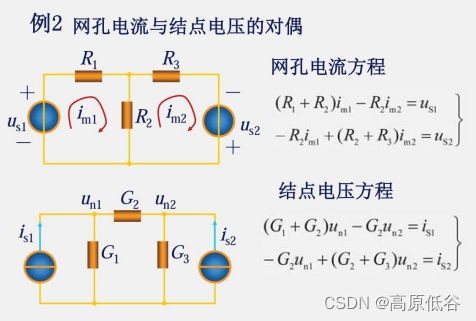
8、对偶定理
七大对偶关系:
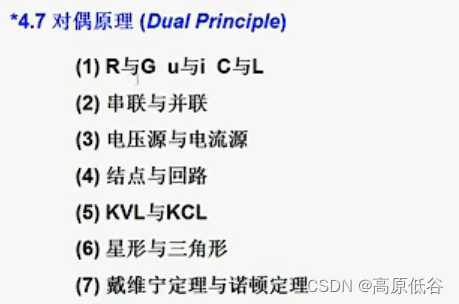
应用对偶原理化繁为简,或在锁上正门的房中,找到后门。
思路是如果电路甲的电压u1求不了,找到它的对偶电路乙,求对应的电流i1。