HDU-7314 2023“钉耙编程”杭电多校赛(4)Data Generation
题目大意
给定 n n n和 m m m,求下面的算法中 a n s ans ans的期望值模 998244353 998244353 998244353后的结果。

有
T
T
T组数据。
1 ≤ T ≤ 1 0 5 , 1 ≤ n ≤ 1 0 18 , 0 ≤ m ≤ 1 0 18 1\leq T\leq 10^5,1\leq n\leq 10^{18},0\leq m\leq 10^{18} 1≤T≤105,1≤n≤1018,0≤m≤1018
数据保证 n n n不是 998244353 998244353 998244353的倍数。
题解
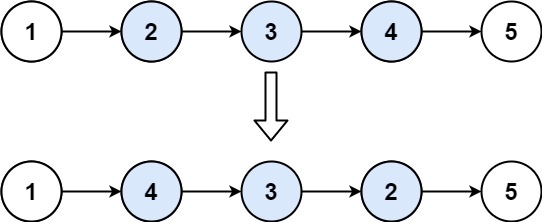
显然对于每个 1 ≤ i ≤ n 1\leq i\leq n 1≤i≤n, m m m次交换后 a i ≠ i a_i\neq i ai=i的概率是相同的,那题意即求 [ a 0 ≠ 0 ] [a_0\neq 0] [a0=0]的期望值 × n \times n ×n,我们只需要求 [ a 0 ≠ 0 ] [a_0\neq 0] [a0=0]的期望值。
设 f i f_i fi表示在第 i i i次交换后 a 0 = 0 a_0=0 a0=0的概率, g i g_i gi表示在第 i i i次交换后 a 0 ≠ 0 a_0\neq 0 a0=0的概率。则递推式如下:
f i = f i − 1 × 1 + ( n − 1 ) 2 n 2 + g i − 1 × 2 n 2 f_i=f_{i-1}\times \dfrac{1+(n-1)^2}{n^2}+g_{i-1}\times \dfrac{2}{n^2} fi=fi−1×n21+(n−1)2+gi−1×n22
g i = f i − 1 × [ 1 − 1 + ( n − 1 ) 2 n 2 ] + g i − 1 × ( 1 − 2 n 2 ) g_i=f_{i-1}\times [1-\dfrac{1+(n-1)^2}{n^2}]+g_{i-1}\times (1-\dfrac{2}{n^2}) gi=fi−1×[1−n21+(n−1)2]+gi−1×(1−n22)
用矩阵优化:
[ f i g i ] = [ 1 + ( n − 1 ) 2 n 2 2 n 2 1 − 1 + ( n − 1 ) 2 n 2 1 − 2 n 2 ] × [ f i − 1 g i − 1 ] \left[ \begin{matrix} f_i \\ g_i \end{matrix} \right]= \left[ \begin{matrix} \frac{1+(n-1)^2}{n^2} & \frac{2}{n^2} \\ 1-\frac{1+(n-1)^2}{n^2} & 1-\frac{2}{n^2} \end{matrix} \right]\times \left[ \begin{matrix} f_{i-1} \\ g_{i-1} \end{matrix} \right] [figi]=[n21+(n−1)21−n21+(n−1)2n221−n22]×[fi−1gi−1]
那么
[ f m g m ] = [ 1 + ( n − 1 ) 2 n 2 2 n 2 1 − 1 + ( n − 1 ) 2 n 2 1 − 2 n 2 ] m × [ f 0 g 0 ] \left[ \begin{matrix} f_m \\ g_m \end{matrix} \right]= \left[ \begin{matrix} \frac{1+(n-1)^2}{n^2} & \frac{2}{n^2} \\ 1-\frac{1+(n-1)^2}{n^2} & 1-\frac{2}{n^2} \end{matrix} \right]^m\times \left[ \begin{matrix} f_0 \\ g_0 \end{matrix} \right] [fmgm]=[n21+(n−1)21−n21+(n−1)2n221−n22]m×[f0g0]
因为 f 0 = 1 f_0=1 f0=1,答案为 n × g m n\times g_m n×gm,所以下列矩阵的第二行第一列的数乘 n n n即为答案。
[ 1 + ( n − 1 ) 2 n 2 2 n 2 1 − 1 + ( n − 1 ) 2 n 2 1 − 2 n 2 ] m \left[ \begin{matrix} \frac{1+(n-1)^2}{n^2} & \frac{2}{n^2} \\ 1-\frac{1+(n-1)^2}{n^2} & 1-\frac{2}{n^2} \end{matrix} \right]^m [n21+(n−1)21−n21+(n−1)2n221−n22]m
这个矩阵可以用矩阵快速幂来求。
时间复杂度为 O ( ∑ log m ) O(\sum \log m) O(∑logm)。
code
#include<bits/stdc++.h>
using namespace std;
const long long mod=998244353;
int T;
long long n,m,ny,p1,p2,p3,p4;
struct matrix{
long long a[2][2];
matrix operator*(const matrix ax)const{
matrix cx;
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
cx.a[i][j]=0;
for(int k=0;k<2;k++){
cx.a[i][j]=(cx.a[i][j]+a[i][k]*ax.a[k][j])%mod;
}
}
}
return cx;
}
}w;
long long in(){
long long t=0,fl=1;
char ch=getchar();
while(ch<'0'||ch>'9') ch=getchar();
while(ch>='0'&&ch<='9'){
t=t*10+ch-'0';ch=getchar();
}
return t*fl;
}
long long mi(long long t,long long v){
if(!v) return 1;
long long re=mi(t,v/2);
re=re*re%mod;
if(v&1) re=re*t%mod;
return re;
}
matrix dd(matrix t,long long v){
matrix re;
re.a[0][1]=re.a[1][0]=0;
re.a[0][0]=re.a[1][1]=1;
while(v){
if(v&1) re=re*t;
v>>=1;t=t*t;
}
return re;
}
int main()
{
T=in();
while(T--){
n=in();m=in();n%=mod;
ny=mi(n,mod-2);
p1=(1+(n-1)*(n-1))%mod*ny%mod*ny%mod;
p2=2*ny*ny%mod;
p3=(1-p1+mod)%mod;
p4=(1-p2+mod)%mod;
w.a[0][0]=p1;w.a[0][1]=p2;
w.a[1][0]=p3;w.a[1][1]=p4;
w=dd(w,m);
printf("%lld\n",w.a[1][0]*n%mod);
}
return 0;
}