目录
1 矩阵加法
1.1 矩阵加法的定义
1.2 加法的属性
1.2.1 只有同类型,相同n*m的矩阵才可以相加
1.2.1 矩阵加法的可交换律:
1.2.2 矩阵加法的可结合律:
1.3矩阵加法的几何意义
2 矩阵的减法
2.1 矩阵减法定义和原理基本同 矩阵的加法
2.2 矩阵减法的几何意义
3 矩阵标量乘法/ 也称 数乘
3.1 数乘的定义
3.2 矩阵的标量乘法的性质,标量乘法/数乘 可交换
3.3 几何意义:就是 正向/方向的伸缩
4 左乘 & 右乘 (很简单概念,但是需要界定语言的严谨性)
4.1 搞清楚主体:谁的左乘?右乘?
4.2 搞清楚方向:什么是左乘和右乘
4.3 一般的线性代数公式 AX=Y, 表示 x 左乘矩阵A
5 矩阵乘法(也称矩阵的点积/内积)
5.1 详细的矩阵乘法规则
5.1.1 计算规则是:
5.1.2 矩阵的乘法不符合交换性,不能交换次序,左乘 ≠ 右乘,A*B ≠B*A
5.2 矩阵内乘/点积的几何意义
6 矩阵的外积?(还不会)
7 矩阵求逆(逆矩阵)
7.1 求逆矩阵的方法
7.2 求逆矩阵的规则
7.2.1 并不是所有的矩阵都可以求逆矩阵
7.3 逆矩阵的几何意义
8 带引号的“矩阵除法”
8.1 一般没有矩阵除法的说法,但可以这么理解
8.2 矩阵除法的几何意义
1 矩阵加法
1.1 矩阵加法的定义
- 矩阵加法一般是指两个矩阵把其相对应元素加在一起的运算。

1.2 加法的属性
可结合律和可交换律
1.2.1 只有同类型,相同n*m的矩阵才可以相加
- (1,2)+(1,2,3) 无法计算
- 如何合法可加,生成的结果也是一个向量
1.2.1 矩阵加法的可交换律:
- A+B=B+A
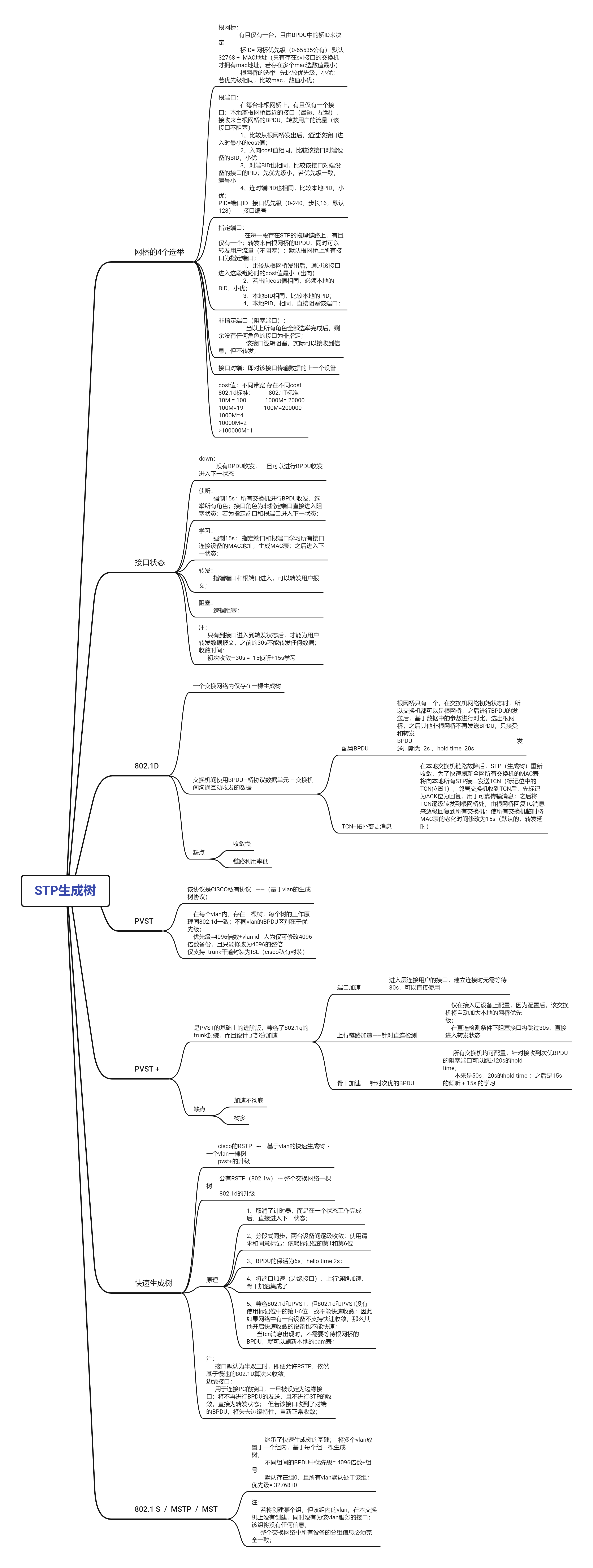
- 看坐标系,表示从上面走先走b,再走a到达C,和从下面先走a,再走b到达C是一样的。
1.2.2 矩阵加法的可结合律:
- (A+B)+C=A+(B+C)
- 看坐标系,表示3个矩阵相加,先计算A+B,再计算A+B+C 和先计算B+C 结果是一样的。
1.3矩阵加法的几何意义
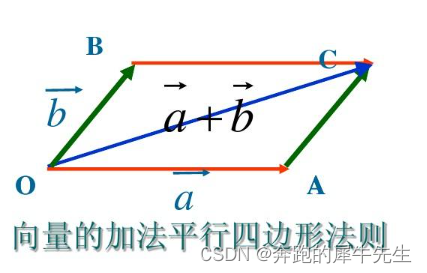
- 看下图,实际是向量的相加,是有方向性的,不是简单的相加
- 而无论2个,还是3个向量相加,都可以用三角形发展继续相加,生成的新向量就是矩阵相加的和----一个新向量


2 矩阵的减法
2.1 矩阵减法定义和原理基本同 矩阵的加法
- 虽然一般不说矩阵减法,但原理上OK,EXCEL里计算也OK

2.2 矩阵减法的几何意义
- 矩阵的减法和加法其实是类似的,但是几何意义不同
- 加法是2个向量,首尾相接,形成新的向量--和向量
- 减法是1个减数向量,开始指向另1个被减数的向量,形成的新向量:差向量。如可以可以挪到原点,从原点出发,
- 可以看出如下图,和从原点出发,而数字为减法后得数的终点作为坐标的向量,是相同的。


3 矩阵标量乘法/ 也称 数乘
3.1 数乘的定义
- λ*(A+B) =λ*A+λ*B
- 就是 标量*矩阵对应位置元素,类整数的乘法
3.2 矩阵的标量乘法的性质,标量乘法/数乘 可交换
- a*X={ax1,ax2,ax3.....axn]
- 交换性 a*X=X*a
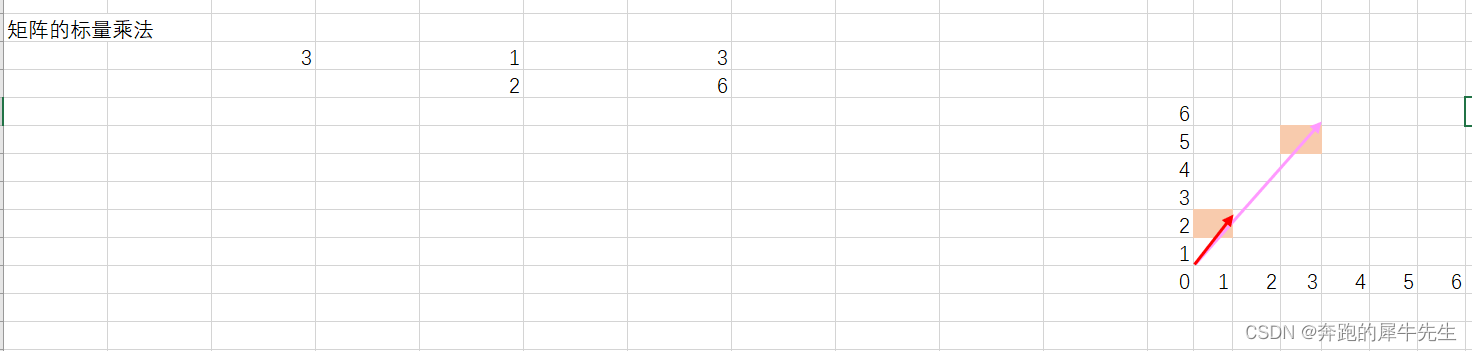
3.3 几何意义:就是 正向/方向的伸缩
- 如果乘以负数,就是反向伸缩
- 如果乘以a>1,就是伸长,
- 如果a=0.5 就是缩短
4 左乘 & 右乘 (很简单概念,但是需要界定语言的严谨性)
4.1 搞清楚主体:谁的左乘?右乘?
- 比如 Ax=y
- 主体:变量? 那变量 x 左乘矩阵A
- 主题,矩阵? 那矩阵A 右乘变量x
4.2 搞清楚方向:什么是左乘和右乘
- A*B ≠ B*A
- A*B 是A右乘B, 是A的右边乘以B
- B*A 是A左乘B,是A的左边乘以B
4.3 一般的线性代数公式 AX=Y, 表示 x 左乘矩阵A
- 一般的线性代数公式 AX=Y, 表示 x 左乘矩阵A
5 矩阵乘法(也称矩阵的点积/内积)
- 在EXCEL里,使用函数 mmult()+ 选择好生成矩阵的长宽区域+数组公式
- 注意要提前计算好 目标矩阵的大小,比如 n*m矩阵* m*k的矩阵,结果是 m*k的矩阵

5.1 详细的矩阵乘法规则
5.1.1 计算规则是:
- 并不是任意2个矩阵都可以相乘
- 只有形如 n*m矩阵* m*k的矩阵的矩阵才可以相乘,也就是前者的列数=后者的行数
- aij= 矩阵1的第i行* 矩阵2的第j列的结果
本质规则
- 是两个矩阵元素的投射形成的新矩阵
5.1.2 矩阵的乘法不符合交换性,不能交换次序,左乘 ≠ 右乘,A*B ≠B*A
- 矩阵乘法要详细考虑次序,不能交换
- A*B ≠ B*A
- 矩阵乘法的具体公式:需要考虑展开,后面详细再说
5.2 矩阵内乘/点积的几何意义
6 矩阵的外积?(还不会)
7 矩阵求逆(逆矩阵)
7.1 求逆矩阵的方法
- 主要是利用 A*A-=I 标准矩阵

7.2 求逆矩阵的规则
7.2.1 并不是所有的矩阵都可以求逆矩阵
- 并不是所有的矩阵都可以求逆矩阵
- 特殊条件是:满秩的双射矩阵才可以求逆
7.3 逆矩阵的几何意义
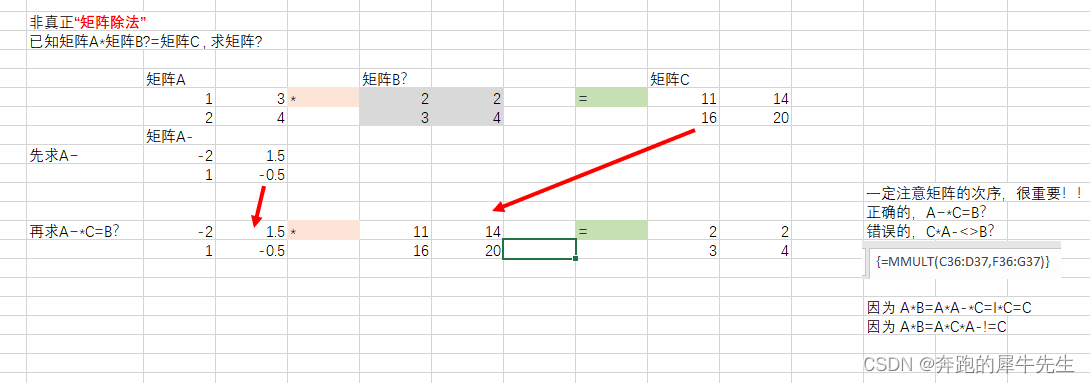
8 带引号的“矩阵除法”
8.1 一般没有矩阵除法的说法,但可以这么理解
- 这个除法实际只是一个类比,并不是真正的 矩阵除法!
这个题目的意思是:
如果知道 ,A矩阵*B矩阵=C矩阵
但是A矩阵已知,C矩阵也已知,如何求B矩阵?
A矩阵*B?矩阵=C矩阵
A*B?=C 那么B?=? 其实B=A-*C 而不是C*A-
- 一定注意矩阵的次序,很重要!!
- 正确的,B=A~*C,而且B !=C*A-
- 错误的,B =C*A-
- 因为如下推导
- A*B= A*A-*C =I*C=C
- A*B= A*C*A- !=C