"养气之学,戒之躁急"
- 1. 3D-2D PNP
- 1.1 代数法
- 1.1.1 DLT(直接线性变换法)
- 1.1.2. P3P
- 1.2 优化法
- BA (Bundle Adjustment)法
- 2. 3D-3D ICP
- 2.1 代数法
- 2.1.1 SVD方法
- 2.2 优化(BA)法
- 2.2.2 非线性优化方法
前置事项:
1. 3D-2D PNP
该问题描述为:当我们知道n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿
1.1 代数法
1.1.1 DLT(直接线性变换法)
解决的问题:已知空间点
P
=
(
X
,
Y
,
Z
,
1
)
T
P = (X, Y, Z, 1)^T
P=(X,Y,Z,1)T 和它投影点
x
1
=
(
u
1
,
v
1
,
1
)
T
x_1 = (u_1, v_1, 1)^T
x1=(u1,v1,1)T。求解相机位姿
R
,
t
\boldsymbol {R, t}
R,t。
为求解,定义增广矩阵
[
R
∣
t
]
=
(
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
8
t
9
t
10
t
11
t
12
)
\boldsymbol {[R| t]} = \begin{pmatrix} t_1&t_2&t_3&t_4 \\\;\\ t_5&t_6&t_7&t_8 \\\;\\ t_9&t_{10}&t_{11}&t_{12} \end{pmatrix}
[R∣t]=
t1t5t9t2t6t10t3t7t11t4t8t12
我们的目的就是求解这个增广矩阵,利用坐标关系得到:
s
(
u
1
v
1
1
)
=
(
t
1
t
2
t
3
t
4
t
5
t
6
t
7
t
8
t
9
t
10
t
11
t
12
)
(
X
Y
Z
1
)
s\begin{pmatrix} u_1&v_1&1 \end{pmatrix} = \begin{pmatrix} t_1&t_2&t_3&t_4 \\\;\\ t_5&t_6&t_7&t_8 \\\;\\ t_9&t_{10}&t_{11}&t_{12} \end{pmatrix}\begin{pmatrix} X&Y&Z&1 \end{pmatrix}
s(u1v11)=
t1t5t9t2t6t10t3t7t11t4t8t12
(XYZ1)
- 最后一行可以求出 s \boldsymbol s s , 则方程中有12个未知数,需要至少六对点, 可以线性变换 ;
- 匹配点大于6对时,可以用SVD等方法对超定方程做最小二乘;
- 缺点:忽略了旋转矩阵自身约束 ----> 找一个旋转矩阵近似(QR分解),把结果重新投影到 S E ( 3 ) SE(3) SE(3) 流形。
1.1.2. P3P
三对(世界坐标系下)3D-2D(成像平面)匹配点 + 一对验证点。原理图如下:

根据相似三角形的相似关系
Δ
O
a
b
−
Δ
O
A
B
,
Δ
O
b
c
−
Δ
O
B
C
,
Δ
O
a
c
−
Δ
O
A
C
⇓
有如下关系
O
A
2
+
O
B
2
−
2
O
A
⋅
O
B
⋅
c
o
s
<
a
,
b
>
=
A
B
2
O
B
2
+
O
C
2
−
2
O
B
⋅
O
C
⋅
c
o
s
<
b
,
c
>
=
B
C
2
O
A
2
+
O
C
2
−
2
O
A
⋅
O
C
⋅
c
o
s
<
a
,
c
>
=
A
C
2
\Delta Oab - \Delta OAB, \quad \Delta Obc - \Delta OBC, \quad \Delta Oac - \Delta OAC \\\;\\\Downarrow 有如下关系 \\\;\\OA^2 + OB^2 -2OA\cdot OB \cdot cos<a,b> = AB^2\\ OB^2 + OC^2 -2OB\cdot OC \cdot cos<b,c> = BC^2 \\ OA^2 + OC^2 -2OA\cdot OC \cdot cos<a,c> = AC^2
ΔOab−ΔOAB,ΔObc−ΔOBC,ΔOac−ΔOAC⇓有如下关系OA2+OB2−2OA⋅OB⋅cos<a,b>=AB2OB2+OC2−2OB⋅OC⋅cos<b,c>=BC2OA2+OC2−2OA⋅OC⋅cos<a,c>=AC2
记
x
=
O
A
/
O
C
,
y
=
O
B
/
O
C
,
v
=
A
B
2
/
O
C
2
,
u
v
=
B
C
2
/
O
C
2
,
w
v
=
A
C
2
/
O
C
2
x=OA/OC\quad, y = OB/OC,\quad v=AB^2/OC^2,\quad uv=BC^2/OC^2,\quad wv=AC^2/OC^2
x=OA/OC,y=OB/OC,v=AB2/OC2,uv=BC2/OC2,wv=AC2/OC2
-
推理可得:
( 1 − u ) y 2 − u x 2 − c o s < b , c > y + 2 u x y ⋅ c o s < a , b > + 1 = 0 ( 1 − w ) x 2 − w y 2 − c o s < a , c > x + 2 w x y ⋅ c o s < a , b > + 1 = 0 (1-u)y^2-ux^2-cos<b,c>y+2uxy\cdot cos<a,b>+1=0 \\(1-w)x^2-wy^2-cos<a,c>x+2wxy\cdot cos<a,b>+1=0 (1−u)y2−ux2−cos<b,c>y+2uxy⋅cos<a,b>+1=0(1−w)x2−wy2−cos<a,c>x+2wxy⋅cos<a,b>+1=0 -
求解完成,其中只有 x , y x,y x,y未知,二元二次方程组,可以用吴氏消化法求解。最终最多得到4个解,用验证点对进行验证,得到正确的点即可。
- 只利用3对点的信息,无法利用更多
- 如果点收到噪声影响,算法失效
- 改进的有 E P n P , U P n P EPnP, UPnP EPnP,UPnP
1.2 优化法
BA (Bundle Adjustment)法
- 利用最小化重投影误差来做,简单来说就是已经有相机位姿,然后用该位姿预测得到预测值,再用 预测减观测(投影) 为误差构建最小二乘问题,重新优化相机位姿和空间点位置。重投影示意图如下:

一种通用做法:用来对PnP或ICP的结果进行优化。
- 假设通过PnP已经获得相机的位姿(不精确的) R , t \boldsymbol {R, t} R,t ,它的李代数为 ξ \boldsymbol \xi ξ;
- n个三维空间点 P i = [ X i , Y i , Z i ] T \boldsymbol P_i = [X_i, Y_i, Z_i]^T Pi=[Xi,Yi,Zi]T ,它的投影坐标为 u i = [ u i , v i ] T \boldsymbol u_i = [u_i, v_i]^T ui=[ui,vi]T ;
用矩阵形式写出像素位置与空间点公式(理论上成立的等式(没有误差时)):
s
i
[
u
i
v
i
1
]
=
K
e
x
p
(
ξ
ˆ
)
[
X
i
Y
i
Z
i
1
]
(
1
)
⇓
即
s
i
u
i
=
K
⋅
e
x
p
(
ξ
ˆ
)
⋅
P
i
(
2
)
⇓
构建最小二乘问题
ξ
∗
=
a
r
g
min
ξ
1
2
∑
i
=
1
n
∥
u
i
−
1
s
i
K
exp
(
ξ
ˆ
)
P
i
∥
2
2
(
3
)
s_i\begin{bmatrix}u_i\\v_i\\1\end{bmatrix} = Kexp(\xi\^{})\begin{bmatrix}X_i\\Y_i\\Z_i\\1\end{bmatrix} \qquad\qquad\qquad\qquad (1)\\\; \Downarrow即\qquad \qquad\qquad\qquad\qquad\\\; \\s_i\boldsymbol u_i = K\cdot exp(\xi\^{})\cdot P_i \qquad \qquad\qquad\qquad\qquad(2)\\\; \\\Downarrow 构建最小二乘问题\qquad \qquad\\\; \\\xi^* = arg\min\limits_\xi \frac{1}{2}\sum\limits_{i=1}^n\begin{Vmatrix}u_i- \frac{1}{s_i} K\exp(\xi\^{})P_i\end{Vmatrix}^2_2\qquad(3)
si
uivi1
=Kexp(ξˆ)
XiYiZi1
(1)⇓即siui=K⋅exp(ξˆ)⋅Pi(2)⇓构建最小二乘问题ξ∗=argξmin21i=1∑n
ui−si1Kexp(ξˆ)Pi
22(3)
在上式中:
- (3)中的 u i \boldsymbol u_i ui :投影位置(观测值---------------------------已知) (2D)
- (2)和(1)中的 u i \boldsymbol u_i ui:重投影位置(预测值-根据(1)式计算得到) (2D)
- P i \boldsymbol {P_i} Pi : 空间点位置(已知) (3D)
重投影误差:用3D和估计位姿投影得到的位置和观测得到的位置作差得到的。实际中利用很多点调整相机位姿使得这个值变小,但不会精确为0.
- 求解这个最小二乘问题,由之前的李代数左乘模型,非线性优化的知识(推理过程略,详见视觉SLAM14讲7.7.3),记变换到相机坐标系下的空间点坐标
P
′
\boldsymbol {P'}
P′ 这里直接给结果:

这个雅克比矩阵描述了重投影误差关于相机位姿李代数的一阶变化关系 ( s e ( 3 ) 这里是平移在前,旋转在后,则如上市,否则前后三列互换 se(3)这里是平移在前,旋转在后,则如上市,否则前后三列互换 se(3)这里是平移在前,旋转在后,则如上市,否则前后三列互换)。
此外,还有 e e e 关于空间点 P P P 的导数:
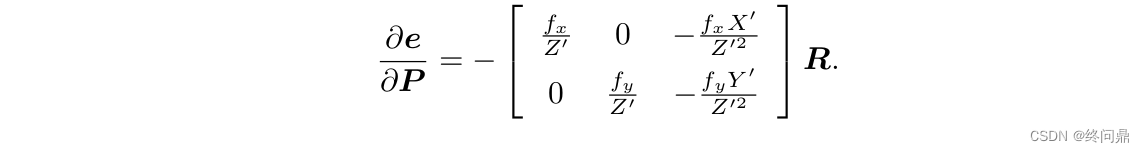
以上两个导数矩阵分别是观测相机方程关于相机位姿和特征点的导数矩阵。在优化中能提供迭代方向。
2. 3D-3D ICP
问题:有一组匹配好的3D点:
P
=
{
p
1
,
.
.
.
,
p
n
}
,
P
′
=
{
p
1
′
,
.
.
.
,
p
n
′
}
P=\left\{p_1, ..., p_n \right\}, \qquad P' = \left\{p'_1, ..., p'_n\right\}
P={p1,...,pn},P′={p1′,...,pn′}
欲求一个欧式变换
R
,
t
R,t
R,t,使:
∀
i
,
p
i
=
R
p
i
′
+
t
{\forall i}, \qquad p_i = Rp'_i + t
∀i,pi=Rpi′+t
用ICP(Iterative Closest Point)求解,没有出现相机模型,和相机无关,故激光SLAM中也有ICP。
2.1 代数法
2.1.1 SVD方法
定义误差:
e
i
=
p
i
−
(
R
p
i
′
+
t
)
e_i = p_i - (Rp'_i + t)
ei=pi−(Rpi′+t)
构建最小二乘问题:使得误差平方和最小
min
R
,
t
J
=
1
2
∑
i
=
1
n
∣
∣
p
i
−
(
R
p
i
′
+
t
)
∣
∣
2
2
\min\limits_{R,t} J = \frac{1}{2}\sum\limits_{i=1}^n||p_i-(Rp'_i+t)||_2^2
R,tminJ=21i=1∑n∣∣pi−(Rpi′+t)∣∣22
求解问题:
- 定义两组点质心
p = 1 n ∑ i = 1 n ( p i ) , p ′ = 1 n ∑ i = 1 n ( p i ′ ) p=\frac{1}{n}\sum\limits_{i=1}^n(p_i),\qquad p'=\frac{1}{n}\sum\limits_{i=1}^n(p'_i) p=n1i=1∑n(pi),p′=n1i=1∑n(pi′) - 带入上边误差最小二乘函数整理,优化后结果:
min R , t J = 1 2 ∑ i = 1 n ∣ ∣ p i − p − R ( p i ′ − p ′ ) ∣ ∣ 2 + ∣ ∣ p − R p ′ − t ∣ ∣ 2 \min\limits_{R,t}J = \frac{1}{2}\sum\limits_{i=1}^n||p_i-p-R(p'_i-p')||^2+||p-Rp'-t||^2 R,tminJ=21i=1∑n∣∣pi−p−R(pi′−p′)∣∣2+∣∣p−Rp′−t∣∣2
观察,左边只和R有关,右边只和质心有关,有R时,令右边等于0,t可得。接下来着重求R - 展开上式中关于
R
R
R 平方项,定义一个
W
W
W,最终用SVD分解可得R,得到后求解t即可。
R = U V T R=UV^T R=UVT
2.2 优化(BA)法
2.2.2 非线性优化方法
和前边介绍的一样,构建G2O,然后导数用李代数扰动模型即可。
min
ξ
=
1
2
∑
i
=
1
n
∣
∣
(
p
i
−
e
x
p
(
ξ
\qquad\qquad\qquad\qquad\qquad\qquad\min\limits_\xi = \frac{1}{2}\sum\limits_{i=1}^n||(p_i-exp(\xi
ξmin=21i=1∑n∣∣(pi−exp(ξ^
)
p
i
′
)
∣
∣
2
2
)\;p'_i)||^2_2
)pi′)∣∣22
注意:在唯一解的情况下,只要我们能找到极小值解,那么该值就是全局最优解。意味着可以任意选取初始值