1. 介绍

1.1 背景

一道面试题：

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中？

在目前为止，我们能想到的最快的办法有两种：

1. 排序+二分查找；
2. 用搜索树如红黑树、哈希表等查找效率非常高的数据结构查找。

虽然从时间复杂度上看，它们的效率还可以，一个是$O(lo{g}_{2}N)$，一个是$log(N)$，但是这个问题从一开始就和一般的查找问题不同：

“40亿个不重复的无符号整数”，在计算机眼中，一个unsigned整数是4个字节（32位机器），那么40亿个就是40亿*4字节，大约是15GB。这么大的数据量，使用哈希表和搜索树都不大可能有效，因为它们作为一种数据结构本身就占有一定的内存空间，例如结点类的大小。每个结点除了数据本身还有其他结构附带的内存空间占用，哈希表能达到45G左右，搜索树更是达到了接近60G。而一般的机器内存并没有这么大，排除第二种方案。

排序+二分查找也不行，还是因为数据量太大，只能作为磁盘文件处理，但是二分查找和外排序都很慢，造成它们速度慢的主要原因是磁盘查找扇区的速度很慢。

即使是强如SSD这样的能够高速读写的固态硬盘，它的读写速度和内存依然相形见绌，所以它的“高速”是相对于传统机械硬盘而言的。

位图就是解决诸如“大海捞针”这样的海量数据问题的。

1.2 概念

位图（bitmap），将每一个bit位的0和1作为集合中某个元素的状态：

• 0：不存在
• 1：存在

常用语海量数据处理和数据查重，是一种较高空间利用率的数据结构。

漫画：Bitmap算法

1.3 应用

1. 快速查找某个数据是否在一个集合中；
2. 排序；
3. 求两个集合的交集、并集等；
4. 操作系统中磁盘块标记；
5. 内核中信号标志位（信号屏蔽字和未决信号集）。
   

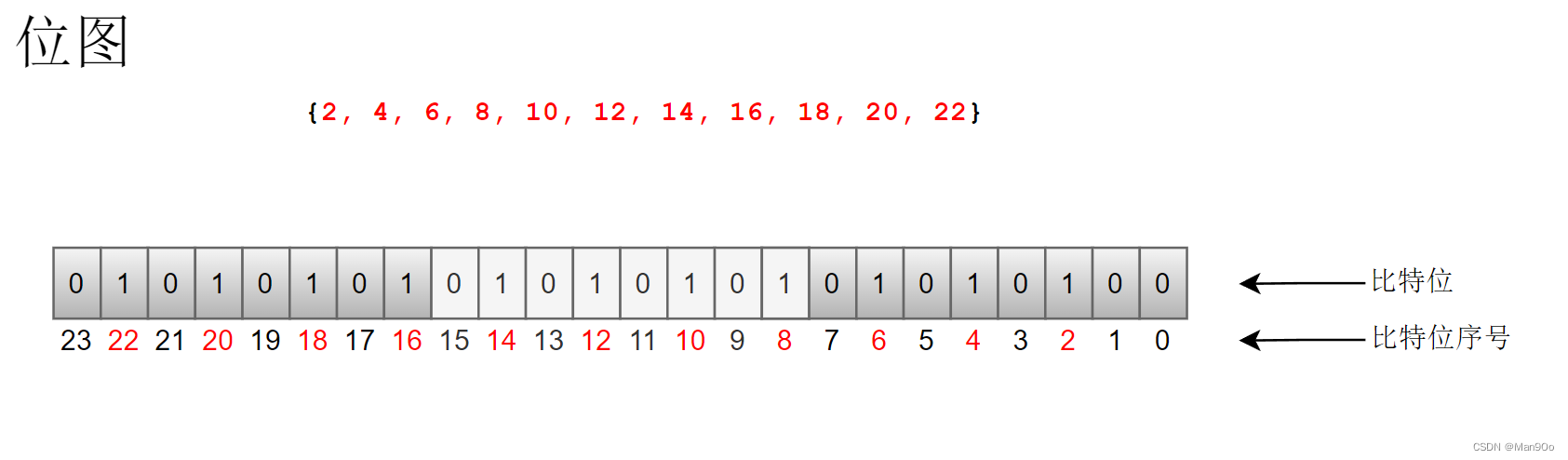
上图中的比特位序号从右到左递增，说明机器是小端机，大多数机器都是小端机。

友情链接：大小端模式

在32位机器中，每个unsigned整数都是4个字节，那么对于上面这个例子，40亿个unsigned整数对应40亿个比特位，一个整数有32个比特位，那么40亿个数也就占512MB。内存消耗极大减少。

2. 位图的使用

STL标准库内置了位图，它叫做bitset。

2.1 原型

template <size_t N> class bitset;

• N：bitset 的大小，以位数表示。

它被包含在头文件<bitset>中。

2.2 构造位图

主要有三种构造位图的方法：

1. 构造一个16位的位图，默认每位都是0：

   bitset<16> bs1; // 0000000000000000
   

2. 用一个具体的数值的二进制序列构造位图：

   bitset<16> bs2(0xffffffff); // 1111111111111111
   

3. （必须）用一个由0和1组成的字符串构造位图：

   bitset<16> bs3(string("1010101001")); // 0000001010101001
   

2.3 常用接口

成员函数	功能
set	设置指定位或所有位
reset	清空指定位或所有位
flip	反转指定位或所有位
test	获取指定位的状态
count	获取被设置位的个数
size	获取可以容纳的位的个数
any	如果有任何一个位被设置则返回true
none	如果没有位被设置则返回true
all	如果所有位都被设置则返回true

2.4 示例

void test1()
{
	bitset<8> bs;
	cout << "bitset<8> bs:" << bs << endl;

	bs.set();			// 设置所有位
	cout << "bs.set():    " << bs << endl;

	bs.flip();			// 反转所有位
	cout << "bs.flip():   " << bs << endl;

	bs.set(1);			// 设置第1位
	cout << "bs.set(1):   " << bs << endl;

	bs.reset(1);		// 清空第1位
	cout << "bs.reset(1): " << bs << endl;

	bs.flip(1);			// 反转第1位
	cout << "bs.flip(1):  " << bs << endl;

	int size = bs.size();// 可表示位的个数
	cout << "bs.size():   " << size << endl;

	bool any = bs.any(); // 任何一个位被设置返回true
	cout << "any be setted:" << any << endl;

	bs.reset();			 // 清空所有位
	bool none = bs.none();// 没有位被设置返回true
	cout << "none be setted:" << none << endl;
}

输出

bitset<8> bs:00000000
bs.set():    11111111
bs.flip():   00000000
bs.set(1):   00000010
bs.reset(1): 00000000
bs.flip(1):  00000010
bs.size():   8
any be setted:1
none be setted:1

2.4 常用运算符

2.4.1 >>和<<

bitset容器重载了>>和<<运算符（流插入和流输出），所以可以直接对容器实例化出的对象进行输入输出操作：

void test2()
{
	bitset<8> bs;
	cin >> bs;
	cout << bs << endl;
}

输入：

1010

输出：

00001010

2.4.2 赋值运算符、关系运算符、复合赋值运算符、单目运算符

• 赋值运算符：=；
• 关系运算符：==、!=；
• 复合赋值运算符：&=、|=、^=、<<=、>>=；
• 单目运算符：~。

void test3()
{
	bitset<8> bs1(string("11100000"));
	bitset<8> bs2(string("00000111"));

	bool eql = bs1 != bs2;
	cout << "bs1!=bs2:  " << eql << endl;

	bs1 >>= 3;
	cout << "bs1>>3:    " << bs1 << endl;

	bs2 ^= bs1;
	cout << "bs2 ^= bs1:" << bs2 << endl;
}

输出：

bs1!=bs2:  1
bs1>>3:    00011100
bs2 ^= bs1:00011011

2.4.3 位运算符

位图也可以直接用三个位运算符对位操作：

void test4()
{
	bitset<8> bs1(string("10101010"));
	bitset<8> bs2(string("01010101"));

	cout << (bs1 & bs2) << endl;
	cout << (bs1 | bs2) << endl;
	cout << (bs1 ^ bs2) << endl;
}

输出：

00000000
11111111
11111111

2.4.4 [ ]运算符

位操作作为计算机中最精细的操作，速度理应是非常快的，所以可以认为是像数组一样随机访问不同序号的比特位：

void test5()
{
	bitset<8> bs(string("10101010"));
	cout << bs[1] << endl;
	bs[7] = 0;
	cout << bs << endl;
}

输出：

1
00101010