推荐语：本文清晰而详细地介绍了如何使用 Parser 组合子方案，结合 Monad 通过合理的分层、抽象和组合，在性能达标的情况下实现消息场景中函数式的表达式解析。非常具有实践意义，推荐阅读学习！

——大淘宝技术终端开发工程师 闲行

什么是表达式引擎

从定义上讲，表达式（Expression）是由代表量的符号和代表运算的符号组成的符合规则的组合。简单地说：
一个良好定义的表达式执行完成会产生一个值。
比如执行表达式 1+2*3 得到结果 7，${version}>10 根据version返回 Bool 值。

代码里的表达式会在编译时编程2进制代码，在运行期得到结果，在某些情况下，我们需要计算字符串形式的表达式，此时解析并执行表达式的程序称为表达式引擎。

为什么需要一个表达式引擎

主要是解决多维度Key导致配置数量爆炸的问题。

一个大型程序往往有一部分配置的数据，可以在程序不变的情况下改变行为。一般情况下，配置方案体现为 Key -> Value的形式，稍微复杂一点，考虑到需要对不同业务进行隔离和管控，会对 Key 进行分组，再复杂一点，需要支持同一个 Key 针对不同的策略有不同的值，比如不同版本的配置不同。

但是消息场景的逻辑更复杂，多维度导致配置数量爆炸，举个例子，消息气泡是否支持转发功能，目前由 消息状态、业务类型、模板类型、模板实例类型四个维度决定，消息状态有5种，业务类型目前有80+，模板类型300+，模板实例类型2000+，Key的值理论上和这些维度是乘积关系，有超过 2亿 种情况，这对于一个配置来说当然是不可接受的。

之前的方案是加入优先级和默认逻辑，即先考虑最细粒度的模板实例类型，如果没有再考虑模板类型，以此按优先级决定是否支持转发，对于不支持转发的，默认为空，默认逻辑本质上是代码也表示了一部分配置。优先级逻辑将 Key 值与维度的关系从乘法变成了加法，配合默认值，我们将转发的配置数量降低到了360多条。

除了转发，考虑到其他长按菜单、页面配置、输入能力等场景，总的配置条数超过了600条，这些配置能不能由代码自动维护呢，答案是不行，因为这些配置都是和产品逻辑相关联的，比如某些消息从支持转发变为不支持转发，类似的产品需求和变更是需要人来执行的，这就带来了很多维护的问题：

1. 内容冗余，配置中存在大量的 Key 具有同样的 Value，导致大量的冗余，存在进一步优化的空间；

2. 规则碎片化，很难理解规则的总和，这是由于这些规则不是独立的，比如想知道转发的完整规则是什么，就必须汇总360多条记录才能得出结果，这就会导致实际规则难以梳理、与产品预期不一致的问题；

3. 变更影响范围大，当规则变化、或者新增 Value 时，需要修改大量已有的配置数据，比如千牛上的商家群、粉丝群等5种需要去掉红包能力，由于输入能力和群成员角色有关，群成员有4个角色，总共需要修改20条配置，大幅增加了出错的概率。如果新增维度涉及到优先级的变化，此时需要修改代码，影响面就变成了所有的配置项，带来大量的测试验证成本和风险；

4. 逻辑实现复杂，对于多维度优先级的逻辑和默认逻辑的支持，以及像自己发送的消息才支持撤回这样的具体逻辑，导致配置与代码边界不清晰，实现逻辑比较复杂，这就会带来可读性、可维护性和稳定性的问题。

通过仔细梳理了这些配置，发现这些这些问题的出现是因为以 Key 的规则为出发点去思考的，而 Key 的逻辑各不相同又不断变化，从而导致了各种问题。很自然的联想到，能不能从 Value 的角度出发，同一个 Value 的配置只有一条，这样就能去掉大量的冗余，另外 Value 是直接表示业务逻辑，Value归一也便于对业务迭代的支持。

这时，Value对应的就不是一个 Key 了，而是多个 Key 的并，这就需要表达式来表示这个并。

表达式的能力

先来看一个简单的表达式：

${bizType} >= 11000 && ${bizType} < 12000

这时用来表示BC场景的表达式，当处于BC聊天页面时，表达式的结果为 true，否则为 false，可以看到，表达式引擎的输入是字符串和环境变量，输出Bool值，因此这是一个解释器的工作，具体来说分为两步：

1. Parse，将表达式解析成一个表达式树；

2. Eval，使用环境变量对表达式树求值。

根据业务场景梳理出表达式需要支持的文法：

expr := expr andor term | term
 andor := && | ||
 term := factor compare factor | factor
 compare := == | >= | > | <= | < | != 
 factor := identifier | num | str | (expr) 
 identifier := "${"{a-zA-z0-9_.}"}"
 str := "\""string"\""
 num := ["-"]{0-9}

表达式1.0的问题

第一个版本的表达式我们使用了苹果的谓词表达式 NSPredicate，成功将规则总条数降低了87%。

使用NSPredicate 遇到了几个问题，比如为了保证规则的双端一致性，采用了业界较为常用的 ${var} 的格式，在 iOS 端需要预处理成 $var 的形式，以及如果变量在调用 evaluateWithObject:substitutionVariables: 时不存在会直接crash，导致老版本功能不正常，我们也进行了发布策略上的兼容。但是在上线使用后，还是遇到了一个无法解决的问题：

NSPredicate不支持嵌套取值，有些业务场景需要使用消息中嵌套较深的数据，如 ${message.ext.templateDynamicData.subscribeInfo.showType} == 6，每次遇到这样的需求都需要编码把数据取出来，再加到环境变量中去，在多次遇到这个问题之后，一方面产生了很多和业务的沟通协作成本，另一方面也让我们参数文档名存实亡；

随着业务多次提出相关的问题，以及在 NSPredicate 上扩展的尝试失败之后，我们决定自己写一个表达式引擎。

新表达式技术方案

▐  Parser 生成器 vs Parser 组合子

对于 Parser 来说，他的任务就是将字符串解析成AST，这在编译原理中一般分为词法分析和语法分析，业界有两种主流的方案，一种是以 Yacc 为代表的 Paser 生成器，一种是以 Parsec 为代表的 Parser 组合子。这两种方案各有优缺点，这里我选择了 Parser 组合子，主要有三个原因，第一是我们解析的是比较简单的上下文无关文法，这个用 Parser 组合子实现起来非常简单，代码完全可控；第二利用 Monad 的抽象让我们免于处理树或栈这些数据结构的状态细节；第三 Parser 组合子能够很方便的扩展解析能力。

▐  提取左因子，消除左递归

上述文法存在两处递归

1: expr := expr andor term | term
2: factor := identifier | num | string | (expr)

第一处为直接左递归，第二处为间接递归，间接递归的问题不需要修改文法，直接左递归可以通过寻找左公共因子解决：

expr := term expr'
expr' := andor expr | nil

然后就可以使用递归下降来解析。

▐  整体方案

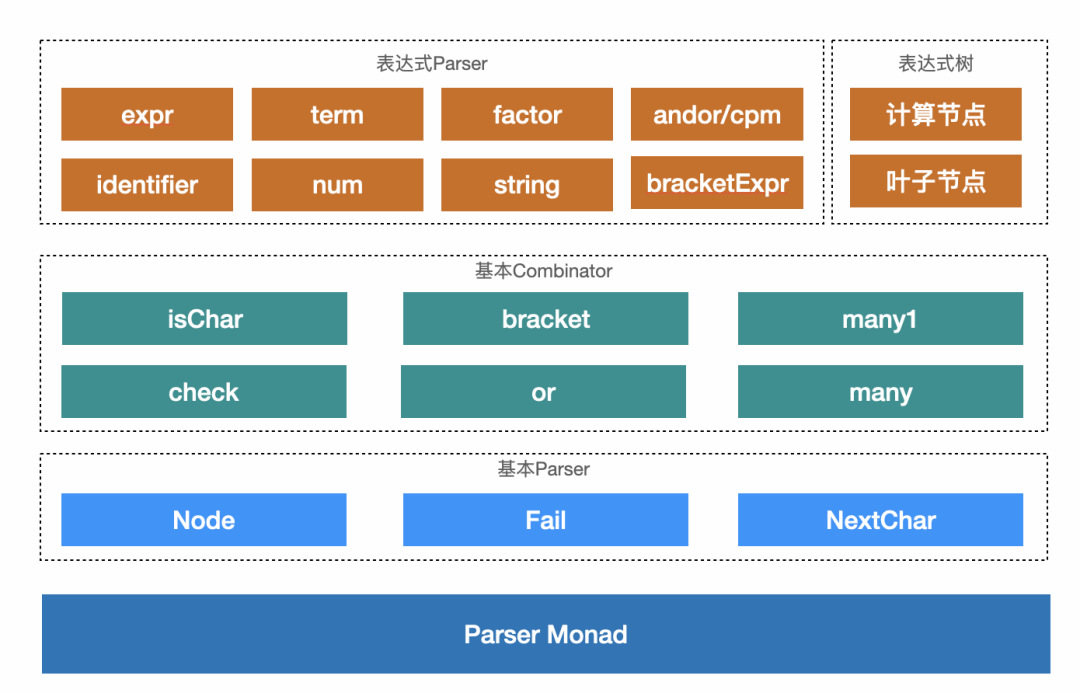
方案整体分为4层，最下面的基础是一个 Parser Monad 的抽象，定义了所有 Parser 的行为，接着第二层基于这个抽象定义了三个基本 Parser 来处理解析成功、失败和继续解析下一个字符的情况，然后第三层定义了用于表示 条件、循环 等解析结构的组合子，这些都是通用的解析能力。

在通用解析能力上，第四层定义了表达式树的叶子结点和计算节点，然后使用表达式树对Parser Monad 进行类型化，根据文法逐层定义对应的 Parser，最终完成了 expr Parser 对整个表达式的解析。

关键表现

▐  Parser 解析的函数抽象

Parser 的抽象分为解析的抽象和组合的抽象。

一步解析本质上是一个函数，一个函数是由输入和输出定义的，一般来说 Parser 输入字符串，输出某种类型的树结构，输入是确定的，对于输出来说，综合考虑一共有三种情况：

1、成功解析了一部分，还有剩余的字符串
2、解析完成
3、解析失败

因此可以利用元组和可空类型，将函数定义为：

public typealias ParserF<A> = (String) -> (A, String)?

当返回具体的元组且String非空时为第一种情况，String空为第二种情况，返回nil为第三种情况。

▐  多个 Parser 的组合

除了函数抽象外，由于大部分Parser只负责解析一部分输入字符串，我们需要一种能够组合两个Parser，并处理表达式树和剩余字符串中间状态的能力，这个能力除了实际操作树结构之外，我们还可以利用Monad实现。

在大多数语言中，Monad体现为一个叫做flatMap的函数，这里抽象完成的Parser定义如下：

// parser定义
public class Parser<A> {
    public let f : ParserF<A>
    init(_ f: @escaping ParserF<A>) {
        self.f = f
    }


    // 对上下文相关的计算进行符合结合律的结合
    public func flatMap<B>(_ f : @escaping ((A) -> Parser<B>)) -> Parser<B> {
        Parser<B> { string in
            self.f(string).flatMap { (a, string2) in
                f(a).f(string2)
            }
        }
    }


    // 执行计算
    public func runParser(_ string : String) -> (A, String)? {
        f(string)
    }
}

这里 flatMap 是一个高阶函数，接受一个函数f，返回一个新的 Parser 。

理解它的关键在于区分这里涉及到的三个函数，第一步是使用自己的函数，对输入字符串 string 做计算，计算出结果 (a，string2)，第二步是将 a 传给 f，获得一个新的 Parser，然后用这个 Parser 的函数对 string2 进行计算。这样做的优势是可以将解析计算进行顺序组合，并将组合和中间状态的维护抽象在这个函数的内部，我们在使用时只关心解析的结果即可，实现了计算本身和计算结果的隔离。

调用 flatMap 只对计算进行了结合，生成了新的计算，计算的执行需要通过 runParser 方法的调用来实现。

▐  三个基本 Parser

完成了 Parser 的抽象后，我们需要实现三个基本的 Parser，然后以此为基础进行组合：

1. 节点 Parser，表示解析成功，使用一个值构造一个节点；

2. 失败 Parser，表示解析失败；

3. 前进 Parser，表示取下一个字符进行解析

// 基本parser
class Node<V> : Parser<V> {
    init(_ v : V) {
        super.init { string in
            (v, string)
        }
    }
}


class Fail<A>: Parser<A> {
    init() {
        super.init { _ in
            (A, String)?.none
        }
    }
}


class NextChar : Parser<Character> {
    init() {
        super.init { string in
            string.firstIndex { c in
                c != " "
            }.flatMap { index in
                (string[index], String(string.suffix(from: string.index(after: index))))
            }
        }
    }
}

可以看到 Parser 的本质就是函数。

▐  定义常用的组合子

在解析的过程中，我们需要用到顺序、条件、循环等结构化编程的能力，但这里我们将通过组合的方式来支持这些能力。

校验组合子，使用一个函数生成一个Parser，用于校验一个字符是否符合定义的条件，相当于解析过程中的if:

public func check(p : @escaping ((Character) -> Bool)) -> Parser<Character> {
    NextChar().flatMap { (c) -> Parser<Character> in
        p(c) ? Node<Character>(c) : Fail<Character>()
    }
}

比如判断是否是某个具体的字符 c，可以通过组合生成 isChar Parser :

public func isChar(_ c : Character) -> Parser<Character> {
    check { c2 in
        c == c2
    }
}

分支组合子，将两个 Parser 组合成一个新的 Parser

其行为是若第一个解析成功就使用第一个，否则使用第二个进行解析，相当于解析过程中的 if..else...。

public func or<A>(_ p1 : Parser<A>, _ p2 : Parser<A>) -> Parser<A> {
    Parser<A> { string in
        p1.runParser(string) ?? p2.runParser(string)
    }
}

文法中还有一些多分支的情况，比如比较大小需要处理 == | >= | > | < | <= | != 6种分支情况，通过 or 组合子会出现多层嵌套，可以对 or 组合子进行扩展支持多个 Parser 的分支组合：

public func first<A>(_ ps : Parser<A>...) -> Parser<A> {
    Parser<A> { string in
        for p in ps {
            if let r = p.runParser(string) {
                return r
            }
        }
        return nil
    }
}

重复组合子，用于一个 Parser 多次解析的情况
比如表达式中很多地方允许任意的空格，这对应了解析过程中类似 While 的循环结构，当然，在 FP 中我们会更多地使用递归版本，当第一个字符解析成功后，再递归调用自己，如果失败，则返回空数组表示递归结束，最后回收递归栈构造解析结果。

public func many<A>(_ p : Parser<A>) -> Parser<[A]> {
    or(
    p.flatMap { a in
        many(p).flatMap { suffix in
            Node([a] + suffix)
        }
    },
    Node([]) //递归终止条件
    )
}

很多时候我们需要至少出现一次的组合子，比如一个自然数，是[0-9]连续出现至少一次，我们可以通过普通 Parser 和 重复组合子的再组合来实现。

public func many1<A>(_ p : Parser<A>) -> Parser<[A]> {
    p.flatMap { a in
        many(p).flatMap { suffix in
            Node([a] + suffix)
        }
    }
}

分支和重复都有了，顺序组合子怎么实现呢

顺序组合其实就是 flatMap， 它实现了对两个 Parser 的顺序组合。以 (expr) 来说，需要先处理 (，再处理expr，再处理 )，这里可以将括号匹配稍微泛化一下：

public func bracket<O, A, C>(open : Parser<O>, p : Parser<A>, close : Parser<C>) -> Parser<A> {
    open.flatMap { _ in
        p.flatMap { a in
            close.flatMap { _ in
                Node(a)
            }
        }
    }
}

▐  定义表达式树

完成通用的解析能力定义，在实现上述文法相关的解析之前，需要对文法解析结果建模。一个合法的表达式解析完成后会产生一个表达式树，在Swift中，树结构可以很方便的用递归枚举来定义 :

public enum Expr2 {
    indirect case AND(Expr2, Expr2)
    indirect case OR(Expr2, Expr2)
    indirect case EQ(Expr2, Expr2)
    indirect case NOTEQ(Expr2, Expr2)
    indirect case BIGTHAN(Expr2, Expr2)
    indirect case BIGEQTHAN(Expr2, Expr2)
    indirect case SMALLEQTHAN(Expr2, Expr2)
    indirect case SMALLTHAN(Expr2, Expr2)
    indirect case BRACKET(Expr2)
    case IDENTIFIER(String)
    case NUM(Int)
    case STRING(String)
}

▐  实现叶子节点的 Parser

叶子结点目前一共有三种 ——identifier\num\string，叶子节点自己就是一个值。有了前面通用的基本Parser和组合子 ，我们就可以来逐个定义它们对应的Parser了，比如identifier := ${string}就可以定义为 :

// 标识符合法值 .46,_95,num48-57,大写65-90,小写97-122
public func isIdentifierChar() -> Parser<Character> {
    check { c in
        let value = c.asciiValue ?? 0
        return value == 46 || value == 95
        || (value >= 48 && value <= 57)
        || (value >= 65 && value <= 90) || (value >= 97 && value <= 122)
    }
}


// 标识符 ${xxx}
public func identifier() -> Parser<Expr2> {
    isChar("$").flatMap { _ in
        isChar("{").flatMap { _ in
            many1(isIdentifierChar()).flatMap { cs in
                isChar("}").flatMap { _ in
                    Node(.IDENTIFIER(String(cs)))
                }
            }
        }
    }
}

作为测试，通过 let treeNode = identifier().runParser("${abc}") 可以成功解析出 Identifier节点。

同理可以定义出 num、str的实现。

可以看到，identifier()的解析过程只涉及解析的结果 cs，而不涉及各种中间的状态和错误的处理，甚至连输入字符串都没出现，这就是 Monad 的优势。

▐  实现计算节点的 Parser

除了叶子节点之外全部是计算节点，计算节点需要根据自己的两个孩子节点计算出值，因此计算节点的值实际上是一个函数，比如 == Parser :

// 计算节点中值的类型
public typealias MakeExpr = (Expr2, Expr2) -> Expr2


// == 对应的函数
func EQ(_ e1 : Expr2, _ e2 : Expr2) -> Expr2 {
    .EQ(e1, e2)
}


// 解析 == 
public func isEq() -> Parser<MakeExpr> {
    isChar("=").flatMap { _ in
        isChar("=").flatMap { _ in
            Node(EQ)
        }
    }
}

同理可以给出 &&、||、==、>=、>、<=、<、!= 等计算节点对应的 Parser。这里只是解析了字符串，生成了计算的表达式树，但是并没有计算。

有了这些基本的计算节点之后，我们就可以与first和or组合出 factor\compare\term\expr'\expr 的定义了：

public func compare() -> Parser<MakeExpr> {
    first(isEq(), notEq(), bigeqthan(), bigthan(), smalleqthan(), smallthan())
}


public func factor() -> Parser<Expr2> {
    first(identifier(), num(), string(), bracketExpr())
}


public func term() -> Parser<Expr2> {
    or(factor().flatMap({ factor1 in
        compare().flatMap { makeExpr in
            factor().flatMap { factor2 in
                Node(makeExpr(factor1, factor2))
            }
        }
    }), factor())
}


public func _expr() -> Parser<PartExpr> {
    or(andor().flatMap({ makeExpr in
        expr().flatMap { expr2 in
            Node { expr1 in
                makeExpr(expr1, expr2)
            }
        }
    }),
       Node{ expr in
        expr
    })
}


public func expr() -> Parser<Expr2> {
    term().flatMap { expr in
        _expr().flatMap { partExpr in
            Node(partExpr(expr))
        }
    }
}

▐  解决 expr\factor\(expr) 的死循环问题

在“实现计算节点的 Parser “节中我们已经完成了所有 Parser 的定义，但是实际运行起来后，发现程序陷入了死循环。

在“提取左因子，消除左递归“节，我们通过提取左因子消除了表达式文法中的左递归，实际上文法中还有一处递归，即 expr 间接调用 factor,  factor 的定义中包含 (expr) ，而(expr)的实现是这样的：

public func bracketExpr2() -> Parser<Expr2> {
    bracket( open: isChar("("), p: expr(), close:isChar(")"))
}

这导致了实际运行过程中的死循环，原因是Swift对函数的参数是严格求值的，在 bracket 调用时就要获得 expr() 的返回值，这里我们通过定义惰性求值版本的 bracket 函数来解决：

public func bracketLazy<O, A, C>(open : Parser<O>, p : @escaping () -> Parser<A>, close : Parser<C>) -> Parser<A> {
    open.flatMap { _ in
        p().flatMap { a in
            close.flatMap { _ in
                Node(a)
            }
        }
    }.setName("()")
}


public func bracketExpr() -> Parser<Expr2> {
    bracketLazy( open: isChar("("), p: { expr() }, close:isChar(")") )
}

最后给 Parser 加一个外部调用的方法，返回解析后的表达式树：

public func parse(_ string : String) -> A? {
    runParser(string).flatMap{$0.0}
}

现在可以调用 parser 函数获取解析成功的表达式树：

let string = "(3<3||5<=5) && ${key.text} == \"456\" && ${type} == 123";
let expr = expr().parse(string)

▐  求值

拿到表达式树之后，可以结合环境变量进行求值，这一步需要对表达式树定义 eval 方法，具体通过模式匹配根据不同的节点分别给出对应的实现即可：

func eval(_ context : [String : Any]?) -> Any? {
    switch self {
    case .AND(let expr1, let expr2):
        return expr1.evalBool(context) && expr2.evalBool(context)
    case .OR(let expr1, let expr2):
        return expr1.evalBool(context) || expr2.evalBool(context)
    case .IDENTIFIER(let str):
        return MPKVC.mpValue(forKeyPath: str, kvcObject: context)
    ......
}

而前面 NSPredicate 的痛点问题也可以在求值环节解决，对于系统 NSPredicate 不支持嵌套取值的问题，我们可以在 case .IDENTIFIER(let str): 使用 KVC 支持，考虑到Swift是一个静态强类型的语言，这里需要借助OC的能力；对于老版本没有${var}对应数据的问题，也可以在求值阶段予以忽略，保证原有逻辑不变。

至此，就完成了整个解析和求值工作。

性能表现

表达式的解析和求值作为一项纯CPU工作，其运行的性能主要看解析和求值时间，使用release包在iPhone7上实测数据（20次平均值）如下：

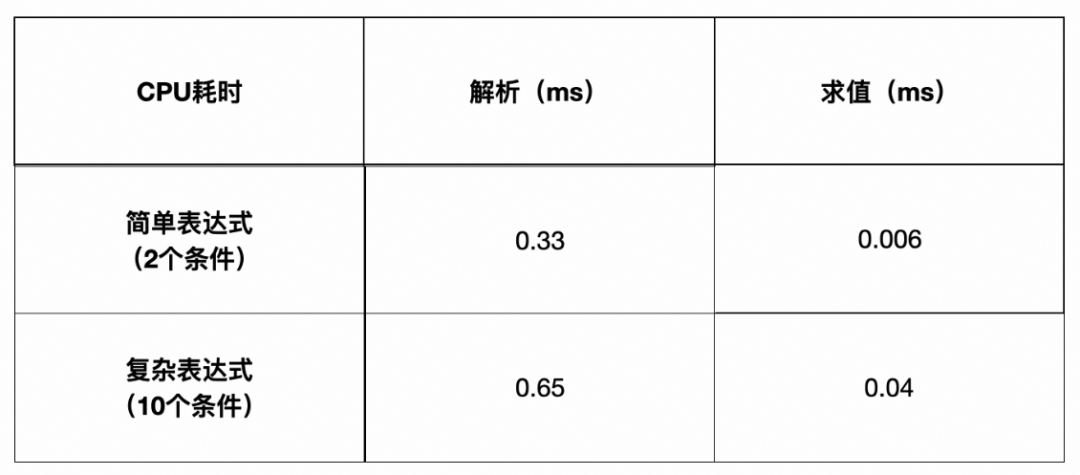
可以得出两个结论:

1. 解析耗时远大于求值耗时，对重复求值的表达式进行缓存可以大大提升性能表现；

2. 目前消息单项业务涉及的表达式，大部分都很简单，最复杂的是长按菜单，一共有8项，首次全部解析+求值在低端机耗时约5ms，后续求值耗时< 0.5ms，性能符合要求。

解析过程的性能，目前来说仍然存在少量的回溯情况，这部分可以通过提取左因子来优化。

再谈 Monad

本文针对表达式引擎的需求，利用 Monad 强大的抽象和组合能力，通过定义 Parser 抽象、基本 Parser、基本组合子、表达式树和表达式 Parser，实现了函数式的表达式解析。

Monad是 FP 中的一个非常重要的抽象，这个概念由 Maclane 于60年代在范畴论中提出，80年代末由 Wadler 等人引入编程领域，随后深刻的影响了 FP 的理念与设计，近些年随着函数式的趋势兴起。在绝大多数场合，这个概念的中文翻译是“单子”，但是和 Convolution 翻译成“卷积”一样很难从名称上理解。

Monad 可以理解为一种容器，里面装了 value 或者 function，通过 flatMap 、bind 或者 >>= 这样的函数对两个 Monad 进行复合，复合之后的结果仍然是一个 Monad，因此可以一直复合下去，flatMap 是一个高阶函数，接受一个函数，这个函数以第一个 Monad 的结果为参数，返回第二个 Monad，从而实现了上下文相关的计算。

Monad 对计算结构进行了抽象，比如说每个 Parser实际上都对应了一个对应字符内容的集合，flatMap 实现了顺序计算的抽象，or 实现了对条件计算的抽象，many 实现了对迭代计算的抽象，这些计算结构是在匹配数字、关键字、字符串中反复出现的。另外整个过程中 Optional Monad 默默地处理掉了错误。

对于编程实践来说，计算结构的抽象将计算中和结果无关的部分隐藏起来，使得在使用时可以只关注结果，实现关注点的分离，使代码的结构更清晰。实际上，Parser Monad 中状态维护和错误处理还可以进一步抽象出 State Monad 和 Optional Monad，这两个 Monad 的组合也可以进一步通过 Monad Transformer 进行抽象，这个过程完全不需要改变上层代码，有兴趣的读者可以试一试。

在 FP 的实践过程中，大部分函数都是很短的，单个看是很简单的，但是复合起来能实现很复杂的功能。我觉得纯函数是很好理解的，高阶函数、柯里化、和类型、函数的组合也不是很难，难的是怎么在计算过程都是纯函数的前提下实现了对状态的维护、错误的处理和对IO副作用的处理，这是 FP 在之前遇到的难题，Monad 给出了一种答案。

References：
https://hackage.haskell.org/package/parsec
https://www.cs.nott.ac.uk/~pszgmh/monparsing.pdf
https://rwh.readthedocs.io/en/latest/

团队介绍

我们是来自大淘宝技术全域触达&用户互动客户端团队，负责包含Push、POP弹层和消息沟通三大触达场景。全域触达&用户互动客户端团队追求极致的性能、流畅的交互体验和稳定的触达效率，用智能化的调控策略为用户带来更好的使用体验。

¤ 拓展阅读 ¤

3DXR技术 | 终端技术 | 音视频技术

服务端技术 | 技术质量 | 数据算法