多元函数微分法及其应用
( 1 )多元函数的极限: 用“ ε − δ ”语言描述,二元函数的极限叫二重极限 二重极限存在: { 1 、 P ( x , y ) 一定要以任何方式趋于 ( x 0 , y 0 ) 时, f ( x , y ) 无限趋近于 A 2 、如果以某一特殊方式(如沿一条定直线或曲线),则不能判定极限存在 3 、如果 P ( x , y ) 以不同方式趋于 ( x 0 , y 0 ) 时, f ( x , y ) 趋于不同的值,则极限不存在 ( 2 )多元函数的连续性: 如果 lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = f ( x 0 , y 0 ) ,则连续 如果在 p 0 ( x 0 , y 0 ) 处不连续,则该点为间断点 ( 3 )偏导数 即使某点的各偏导数存在,也不能保证在该点连续,这是因为偏导数存在只能保证沿着坐标轴的方向趋于该点 二阶偏导数:有四个 混合偏导数相等,与求导次序无关 ( 4 )全微分 偏增量:即某一自变量固定,另一自变量取得增量时函数值的差,即 f ( x + Δ x , y ) − f ( x , y ) 偏微分:偏增量的线性主部,即 f ( x + Δ x , y ) − f ( x , y ) ≈ f x ( x , y ) Δ x 全增量: Δ z = f ( x + Δ x , y + Δ y ) − f ( x , y ) 全微分: Δ z = A Δ x + B Δ y + o ( ( Δ x ) 2 + ( Δ y ) 2 ) ,为两个偏微分之和 全微分为什么这么写,可以这样想: 点先沿 x 轴方向移动了 Δ x 则函数值改变了 A Δ x ,这是一元函数微分学中的概念,用直线代替曲线 然后点再沿 y 轴方向移动了 Δ y 此时函数值又改变了 B Δ y ,那么总的函数值不就行改变了 A Δ x + B Δ y 嘛 为什么是 ( Δ x ) 2 + ( Δ y ) 2 的高阶无穷小呢?因为当 Δ x → 0 , Δ y → 0 时,意味着两点距离趋于 0 如果在某点可微,则该点连续,且各偏导数存在,且 A = ∂ z ∂ x , B = ∂ z ∂ y 如果各偏导数存在,那么该点不一定可微;如果该点连续,也不一定可微 若各偏导数存在且连续(在该点的某个领域存在),则该点可微 一元导数与多元函数复合: 全导数: d z d t = ∂ z ∂ u d u d t + ∂ z ∂ v d v d t 多元函数与多元函数复合: ∂ z ∂ x = ∂ z ∂ u ∂ u ∂ x + ∂ z ∂ v ∂ v ∂ x , ∂ z ∂ y = ∂ z ∂ u ∂ u ∂ y + ∂ z ∂ v ∂ v ∂ y (1)多元函数的极限:\\ 用“\varepsilon-\delta”语言描述,二元函数的极限叫二重极限 \\ 二重极限存在:\\ \begin{cases} 1、P(x,y)一定要以任何方式趋于(x_0,y_0)时,f(x,y)无限趋近于A \\ 2、如果以某一特殊方式(如沿一条定直线或曲线),则不能判定极限存在 \\ 3、如果P(x,y)以不同方式趋于(x_0,y_0)时,f(x,y)趋于不同的值,则极限不存在 \\ \end{cases} \\ \,\\ (2)多元函数的连续性:\\ 如果\lim_{(x,y) \to (x_0,y_0)}f(x,y)=f(x_0,y_0),则连续 \\ 如果在p_0(x_0,y_0)处不连续,则该点为间断点 \\ \,\\ (3)偏导数 \\ 即使某点的各偏导数存在,也不能保证在该点连续,这是因为偏导数存在只能保证沿着坐标轴的方向趋于该点 \\ 二阶偏导数:有四个 \\ 混合偏导数相等,与求导次序无关 \\ \,\\ (4)全微分 \\ 偏增量:即某一自变量固定,另一自变量取得增量时函数值的差,即f(x+\Delta x,y)-f(x,y) \\ 偏微分:偏增量的线性主部,即f(x+\Delta x,y)-f(x,y) \approx f_x(x,y)\Delta x \\ 全增量:\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y) \\ \,\\ 全微分:\Delta z=A\Delta x+B\Delta y+o(\sqrt{(\Delta x)^2+(\Delta y)^2}),为两个偏微分之和 \\ 全微分为什么这么写,可以这样想:\\ 点先沿x轴方向移动了\Delta x则函数值改变了A\Delta x,这是一元函数微分学中的概念,用直线代替曲线 \\ 然后点再沿y轴方向移动了\Delta y此时函数值又改变了B\Delta y,那么总的函数值不就行改变了A\Delta x+B\Delta y嘛\\ 为什么是\sqrt{(\Delta x)^2+(\Delta y)^2}的高阶无穷小呢?因为当\Delta x \to 0,\Delta y \to 0时,意味着两点距离趋于0 \,\\ 如果在某点可微,则该点连续,且各偏导数存在,且A=\frac{\partial z}{\partial x},B=\frac{\partial z}{\partial y} \\ 如果各偏导数存在,那么该点不一定可微;如果该点连续,也不一定可微\\ 若各偏导数存在且连续(在该点的某个领域存在),则该点可微 \\ \,\\ 一元导数与多元函数复合:\\ 全导数:\frac{dz}{dt}=\frac{\partial z}{\partial u}\frac{du}{dt}+\frac{\partial z}{\partial v}\frac{dv}{dt} \\ 多元函数与多元函数复合:\\ \frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial x},\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial y} (1)多元函数的极限:用“ε−δ”语言描述,二元函数的极限叫二重极限二重极限存在:⎩ ⎨ ⎧1、P(x,y)一定要以任何方式趋于(x0,y0)时,f(x,y)无限趋近于A2、如果以某一特殊方式(如沿一条定直线或曲线),则不能判定极限存在3、如果P(x,y)以不同方式趋于(x0,y0)时,f(x,y)趋于不同的值,则极限不存在(2)多元函数的连续性:如果(x,y)→(x0,y0)limf(x,y)=f(x0,y0),则连续如果在p0(x0,y0)处不连续,则该点为间断点(3)偏导数即使某点的各偏导数存在,也不能保证在该点连续,这是因为偏导数存在只能保证沿着坐标轴的方向趋于该点二阶偏导数:有四个混合偏导数相等,与求导次序无关(4)全微分偏增量:即某一自变量固定,另一自变量取得增量时函数值的差,即f(x+Δx,y)−f(x,y)偏微分:偏增量的线性主部,即f(x+Δx,y)−f(x,y)≈fx(x,y)Δx全增量:Δz=f(x+Δx,y+Δy)−f(x,y)全微分:Δz=AΔx+BΔy+o((Δx)2+(Δy)2),为两个偏微分之和全微分为什么这么写,可以这样想:点先沿x轴方向移动了Δx则函数值改变了AΔx,这是一元函数微分学中的概念,用直线代替曲线然后点再沿y轴方向移动了Δy此时函数值又改变了BΔy,那么总的函数值不就行改变了AΔx+BΔy嘛为什么是(Δx)2+(Δy)2的高阶无穷小呢?因为当Δx→0,Δy→0时,意味着两点距离趋于0如果在某点可微,则该点连续,且各偏导数存在,且A=∂x∂z,B=∂y∂z如果各偏导数存在,那么该点不一定可微;如果该点连续,也不一定可微若各偏导数存在且连续(在该点的某个领域存在),则该点可微一元导数与多元函数复合:全导数:dtdz=∂u∂zdtdu+∂v∂zdtdv多元函数与多元函数复合:∂x∂z=∂u∂z∂x∂u+∂v∂z∂x∂v,∂y∂z=∂u∂z∂y∂u+∂v∂z∂y∂v
隐函数的求导公式
上册中的隐函数部分,只告诉了我们隐函数求导只需要方程两边分别对 x 求导即可 而下册介绍了隐函数存在定理和隐函数求导公式: d y d x = − F x F y 隐函数存在定理 1 :有函数 F ( x , y ) ,如果 F ( x 0 , y 0 ) = 0 且 F y ( x 0 , y 0 ) ≠ 0 ,则方程 F ( x , y ) = 0 在 ( x 0 , y 0 ) 处能确定一个隐函数 y = f ( x ) 对于三元方程,则有如下定理: 隐函数存在定理 2 :有函数 F ( x , y , z ) ,如果 F ( x 0 , y 0 , z 0 ) = 0 且 F z ( x 0 , y 0 , z 0 ) ≠ 0 ,则方程 F ( x , y , z ) = 0 在 ( x 0 , y 0 , z 0 ) 处能确定一个二元函数 y = f ( x , y ) 且 ∂ z ∂ x = − F x F z , ∂ z ∂ y = − F y F z 克莱默法则: 适用情形: n 个方程, n 个未知元,有唯一解 如何判断有没有唯一解 : 系数行列式不为 0 就有唯一解 如: { 3 x 1 − 2 x 2 = 12 2 x 1 + x 2 = 1 ,此时 x 1 = D 1 D , x 2 = D 2 D D = ∣ 3 − 2 2 1 ∣ = 7 ≠ 0 , D 1 = ∣ 12 − 2 1 1 ∣ , D 2 = ∣ 3 12 2 1 ∣ 方程组情形: { F ( x , y , z ) = 0 G ( x , y , z ) = 0 ,两个方程,三个未知元,则 x 是自变量, y 和 z 都是关于 x 的一元函数 { F ( x , y , u , v ) = 0 G ( x , y , u , v ) = 0 ,两个方程,四个未知元,则 x 、 y 是自变量, u 和 v 都是关于 x 、 y 的二元函数 例题:设 x u − y v = 0 , y u + x v = 1 ,求 ∂ u ∂ x 、 ∂ v ∂ x 、 ∂ u ∂ y 、 ∂ v ∂ y 方程组两边对 x 求导并移项,得 { x ∂ u ∂ x − y ∂ v ∂ x = − u y ∂ u ∂ x + x ∂ v ∂ x = − v 然后运用克莱默法则求 ∂ u ∂ x 和 ∂ v ∂ x 即可 上册中的隐函数部分,只告诉了我们隐函数求导只需要方程两边分别对x求导即可 \\ 而下册介绍了隐函数存在定理和隐函数求导公式:\frac{dy}{dx}=-\frac{F_x}{F_y} \\ 隐函数存在定理1:有函数F(x,y),如果F(x_0,y_0)=0且F_y(x_0,y_0) \neq 0,则方程F(x,y)=0在(x_0,y_0)处能确定一个隐函数y=f(x) \\ \,\\ 对于三元方程,则有如下定理:\\ 隐函数存在定理2:有函数F(x,y,z),如果F(x_0,y_0,z_0)=0且F_z(x_0,y_0,z_0) \neq 0,则方程F(x,y,z)=0在(x_0,y_0,z_0)处能确定一个二元函数y=f(x,y) \\ 且\frac{\partial z}{\partial x}=-\frac{F_x}{F_z},\frac{\partial z}{\partial y}=-\frac{F_y}{F_z} \\ \,\\ 克莱默法则:\\ 适用情形:n个方程,n个未知元,有唯一解 \\ 如何判断有没有唯一解:系数行列式不为0就有唯一解 \\ 如: \begin{cases} 3x_1-2x_2=12 \\ 2x_1+x_2=1 \end{cases}, 此时x_1=\frac{D_1}{D},x_2=\frac{D_2}{D} \\ D= \begin{vmatrix} 3 & -2 \\ 2 &1 \end{vmatrix}=7 \neq 0, D_1= \begin{vmatrix} 12 & -2 \\ 1 &1 \end{vmatrix}, D_2= \begin{vmatrix} 3 & 12 \\ 2 &1 \end{vmatrix} \\ \,\\ 方程组情形:\\ \begin{cases} F(x,y,z)=0 \\ G(x,y,z)=0 \end{cases}, 两个方程,三个未知元,则x是自变量,y和z都是关于x的一元函数 \\ \begin{cases} F(x,y,u,v)=0 \\ G(x,y,u,v)=0 \end{cases}, 两个方程,四个未知元,则x、y是自变量,u和v都是关于x、y的二元函数 \\ 例题:设xu-yv=0,yu+xv=1,求\frac{\partial u}{\partial x}、\frac{\partial v}{\partial x}、\frac{\partial u}{\partial y}、\frac{\partial v}{\partial y} \\ 方程组两边对x求导并移项,得 \begin{cases} x\frac{\partial u}{\partial x}-y\frac{\partial v}{\partial x}=-u \\ y\frac{\partial u}{\partial x}+x\frac{\partial v}{\partial x}=-v \end{cases} 然后运用克莱默法则求\frac{\partial u}{\partial x}和\frac{\partial v}{\partial x}即可 上册中的隐函数部分,只告诉了我们隐函数求导只需要方程两边分别对x求导即可而下册介绍了隐函数存在定理和隐函数求导公式:dxdy=−FyFx隐函数存在定理1:有函数F(x,y),如果F(x0,y0)=0且Fy(x0,y0)=0,则方程F(x,y)=0在(x0,y0)处能确定一个隐函数y=f(x)对于三元方程,则有如下定理:隐函数存在定理2:有函数F(x,y,z),如果F(x0,y0,z0)=0且Fz(x0,y0,z0)=0,则方程F(x,y,z)=0在(x0,y0,z0)处能确定一个二元函数y=f(x,y)且∂x∂z=−FzFx,∂y∂z=−FzFy克莱默法则:适用情形:n个方程,n个未知元,有唯一解如何判断有没有唯一解:系数行列式不为0就有唯一解如:{3x1−2x2=122x1+x2=1,此时x1=DD1,x2=DD2D= 32−21 =7=0,D1= 121−21 ,D2= 32121 方程组情形:{F(x,y,z)=0G(x,y,z)=0,两个方程,三个未知元,则x是自变量,y和z都是关于x的一元函数{F(x,y,u,v)=0G(x,y,u,v)=0,两个方程,四个未知元,则x、y是自变量,u和v都是关于x、y的二元函数例题:设xu−yv=0,yu+xv=1,求∂x∂u、∂x∂v、∂y∂u、∂y∂v方程组两边对x求导并移项,得{x∂x∂u−y∂x∂v=−uy∂x∂u+x∂x∂v=−v然后运用克莱默法则求∂x∂u和∂x∂v即可
多元函数微分学的几何应用
( 1 )一元向量值函数(普通一元函数的推广) 映射 f : D → R n ,记为 r = f ( t ) = x i + y j + z k = f 1 ( t ) i + f 2 ( t ) j + f 3 ( t ) k 向量值函数的极限定义: 对任意给定的正数 ϵ ,总存在正数 δ ,当 0 < ∣ t − t 0 ∣ < δ 时, ∣ f ( t ) − r 0 ∣ < ϵ ,则 r 0 是极限 极限存在的充要条件:三个分量函数的极限都存在 向量值函数连续的定义: 若 lim t → t 0 f ( t ) = f ( t 0 ) 则连续 连续的充要条件:三个分量函数都连续 向量值函数的导数(或导向量)的定义: lim Δ t → 0 Δ r Δ t = lim Δ t → 0 f ( t 0 + Δ t ) − f ( t 0 ) Δ t 可导的充要条件:三个分量函数都可导,其导数 f ′ ( t 0 ) = f 1 ′ ( t 0 ) i + f 2 ′ ( t 0 ) j + f 3 ′ ( t 0 ) k 向量值函数导数的运算法则: d d t [ u ( t ) × v ( t ) ] = u ′ ( t ) × v ( t ) + u ( t ) × v ′ ( t ) 导向量的几何意义:是空间曲线在点 M 处的切向量,且指向与 t 的增长方向一致 ( 2 )空间曲线的切线与法平面方程: x − x 0 f 1 ′ ( t ) = y − y 0 f 2 ′ ( t ) = z − z 0 f 3 ′ ( t ) ( x − x 0 ) f 1 ′ ( t ) + ( y − y 0 ) f 2 ′ ( t ) + ( z − z 0 ) f 3 ′ ( t ) ) = 0 ( 3 )曲面的切平面与法线 对于曲面 F ( x , y , z ) = 0 ,其法向量为 ( F x , F y , F z ) (1)一元向量值函数(普通一元函数的推广) \\ 映射f:D \to R^n,记为r=f(t)=xi+yj+zk=f_1(t)i+f_2(t)j+f_3(t)k \\ \,\\ 向量值函数的极限定义:\\ 对任意给定的正数\epsilon,总存在正数\delta,当0<|t-t_0|<\delta 时,|f(t)-r_0|<\epsilon,则r_0是极限 \\ 极限存在的充要条件:三个分量函数的极限都存在 \\ \,\\ 向量值函数连续的定义:\\ 若\lim_{t \to t_0}f(t)=f(t_0)则连续 \\ 连续的充要条件:三个分量函数都连续 \\ \,\\ 向量值函数的导数(或导向量)的定义:\\ \lim_{\Delta t \to 0}\frac{\Delta r}{\Delta t}=\lim_{\Delta t \to 0}\frac{f(t_0+\Delta t)-f(t_0)}{\Delta t} \\ 可导的充要条件:三个分量函数都可导,其导数f'(t_0)=f_1'(t_0)i+f_2'(t_0)j+f_3'(t_0)k \\ \,\\ 向量值函数导数的运算法则:\\ \frac{d}{dt}[u(t)×v(t)]=u'(t)×v(t)+u(t)×v'(t) \\ \,\\ 导向量的几何意义:是空间曲线在点M处的切向量,且指向与t的增长方向一致 \\ \,\\ (2)空间曲线的切线与法平面方程:\\ \frac{x-x_0}{f_1'(t)}=\frac{y-y_0}{f_2'(t)}=\frac{z-z_0}{f_3'(t)} \\ (x-x_0)f_1'(t)+(y-y_0)f_2'(t)+(z-z_0)f_3'(t))=0 \\ \,\\ (3)曲面的切平面与法线 \\ 对于曲面F(x,y,z)=0,其法向量为(F_x,F_y,F_z) (1)一元向量值函数(普通一元函数的推广)映射f:D→Rn,记为r=f(t)=xi+yj+zk=f1(t)i+f2(t)j+f3(t)k向量值函数的极限定义:对任意给定的正数ϵ,总存在正数δ,当0<∣t−t0∣<δ时,∣f(t)−r0∣<ϵ,则r0是极限极限存在的充要条件:三个分量函数的极限都存在向量值函数连续的定义:若t→t0limf(t)=f(t0)则连续连续的充要条件:三个分量函数都连续向量值函数的导数(或导向量)的定义:Δt→0limΔtΔr=Δt→0limΔtf(t0+Δt)−f(t0)可导的充要条件:三个分量函数都可导,其导数f′(t0)=f1′(t0)i+f2′(t0)j+f3′(t0)k向量值函数导数的运算法则:dtd[u(t)×v(t)]=u′(t)×v(t)+u(t)×v′(t)导向量的几何意义:是空间曲线在点M处的切向量,且指向与t的增长方向一致(2)空间曲线的切线与法平面方程:f1′(t)x−x0=f2′(t)y−y0=f3′(t)z−z0(x−x0)f1′(t)+(y−y0)f2′(t)+(z−z0)f3′(t))=0(3)曲面的切平面与法线对于曲面F(x,y,z)=0,其法向量为(Fx,Fy,Fz)
方向导数与梯度
定理:
如果函数
f
(
x
,
y
)
在点
P
0
(
x
0
,
y
0
)
可微分,那么函数在该点沿任一方向
l
的方向导数都存在
且有
∂
f
∂
l
∣
(
x
0
,
y
0
)
=
f
x
(
x
0
,
y
0
)
cos
α
+
f
y
(
x
0
,
y
0
)
cos
β
,
α
和
β
是方向
l
的方向角
梯度向量:
g
r
a
d
f
(
x
0
,
y
0
)
=
∇
f
(
x
0
,
y
0
)
=
f
x
(
x
0
,
y
0
)
i
+
f
y
(
x
0
,
y
0
)
j
∇
=
∂
∂
x
i
+
∂
∂
y
j
称为二维的向量微分算子或
N
a
b
l
a
算子
∂
f
∂
l
∣
(
x
0
,
y
0
)
=
f
x
(
x
0
,
y
0
)
cos
α
+
f
y
(
x
0
,
y
0
)
cos
β
=
g
r
a
d
f
(
x
0
,
y
0
)
⋅
e
l
=
∣
g
r
a
d
f
(
x
0
,
y
0
)
∣
cos
θ
θ
是梯度向量与方向
l
的夹角,因此由如下几种特殊情况:
{
θ
=
0
,方向导数最大,表明函数在某点的方向导数最大的方向是与梯度向量同向的方向
θ
=
π
,是函数在该点的方向导数最小的方向,在该方向函数值减小最快
θ
=
π
2
,函数在该点的方向导数为
0
,即函数值在该方向没有变化
导向量(切向量)、梯度向量和方向导数的几何含义:
假设曲线
T
在三维空间中的参数方程为:
{
x
=
t
y
=
2
t
z
=
−
t
2
+
4
则曲线
T
的向量值函数为
f
(
t
)
=
t
⋅
i
+
2
t
⋅
j
+
(
−
t
2
+
4
)
⋅
k
,导向量
f
′
(
t
0
)
=
i
+
2
j
+
(
−
2
t
0
)
⋅
k
令
t
0
=
1
且
Δ
t
<
0
,则点
M
坐标为
(
1
,
2
,
3
)
,且
M
点导向量
f
′
(
t
0
)
=
f
′
(
1
)
=
−
i
−
2
j
+
2
k
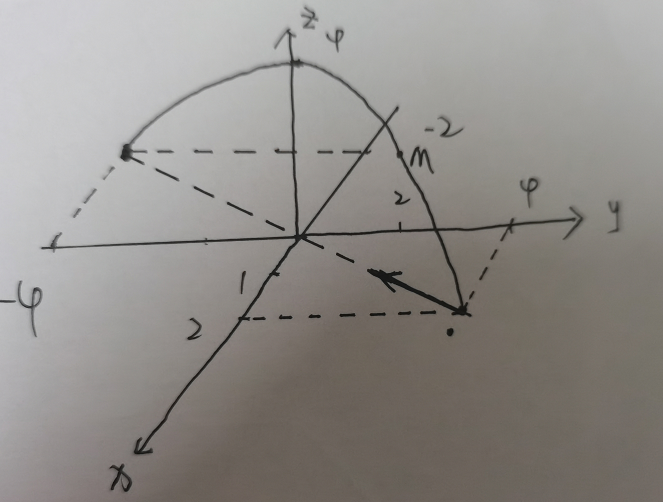
如图
1
所示,为曲线
T
的大致图形。该曲线始终在
y
=
2
x
平面内,投影也始终在
y
=
2
x
这条直线上
而下面讲的方向导数和梯度向量和这个没关系,方向导数与梯度向量是对于曲面而言的,
梯度向量的表达式含有偏导数,而偏导数和向量值函数的分量函数的导数意义是不同的,
比如
f
x
(
x
0
,
y
0
)
与上面的
x
′
就不同,
f
x
(
x
0
,
y
0
)
是
z
对
x
的偏导数,而
x
′
是
x
对
t
的导数,
并且梯度向量的大小、方向与向量
(
x
′
,
y
′
)
的大小、方向都不同
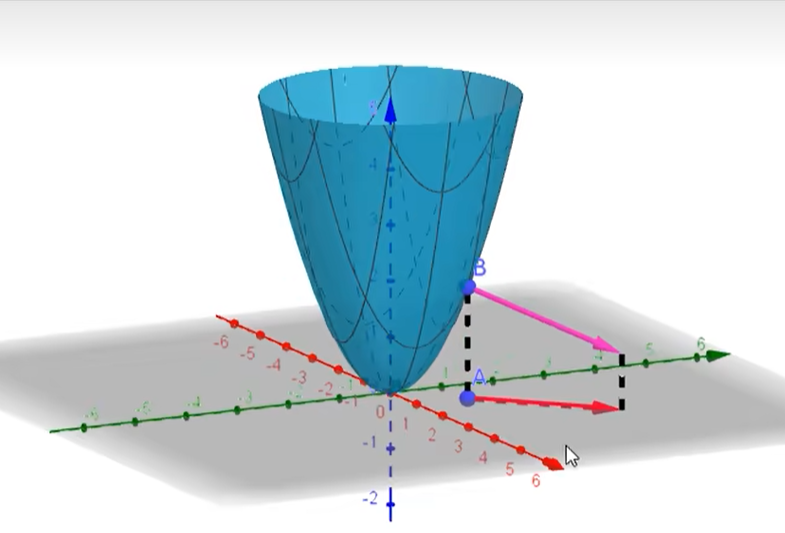
下面再介绍梯度向量的几何意义
其实际上就是曲面上某一点的切面的法向量在
x
O
y
平面上的投影,如图
2
所示
因为垂直于法线投影的的方向会将曲面切割为一个等值线,因此方向导数为
0
,而垂直的话肯定就最大了因为等值线一直在最大限度的变化
前面介绍过曲面切面的法向量为
(
F
x
,
F
y
,
F
z
)
,而梯度向量为
(
∂
z
∂
x
,
∂
z
∂
y
)
,
F
x
等于
∂
z
∂
x
吗,下面来证明一下
为了证实普遍性,创造一个复杂点的函数
x
2
+
3
y
+
x
z
=
0
,
求得
F
x
=
x
2
−
3
y
x
,
F
y
=
3
,
∂
z
∂
x
=
3
y
−
x
2
x
2
,
∂
z
∂
y
=
−
3
x
F
x
F
y
=
∂
z
∂
x
/
∂
z
∂
y
,因此成立
梯度的模
=
该梯度方向的方向导数,即
f
x
2
+
f
y
2
=
f
x
cos
α
+
f
y
cos
β
定理:\\ 如果函数f(x,y)在点P_0(x_0,y_0)可微分,那么函数在该点沿任一方向l的方向导数都存在 \\ 且有\frac{\partial f}{\partial l}\vert_{(x_0,y_0)}=f_x(x_0,y_0)\cos \alpha+f_y(x_0,y_0)\cos \beta,\alpha和\beta是方向l的方向角 \\ \,\\ 梯度向量:grad\,f(x_0,y_0)=\nabla\,f(x_0,y_0)=f_x(x_0,y_0)i+f_y(x_0,y_0)j \\ \nabla=\frac{\partial}{\partial x}i+\frac{\partial}{\partial y}j称为二维的向量微分算子或Nabla算子 \\ \frac{\partial f}{\partial l}\vert_{(x_0,y_0)}=f_x(x_0,y_0)\cos \alpha+f_y(x_0,y_0)\cos \beta=grad\,f(x_0,y_0)\cdot e_l=|grad\,f(x_0,y_0)|\cos \theta \\ \theta是梯度向量与方向l的夹角,因此由如下几种特殊情况:\\ \begin{cases} \theta=0,方向导数最大,表明函数在某点的方向导数最大的方向是与梯度向量同向的方向 \\ \theta=\pi,是函数在该点的方向导数最小的方向,在该方向函数值减小最快 \\ \theta=\frac{\pi}{2},函数在该点的方向导数为0,即函数值在该方向没有变化 \end{cases} \\ \,\\ 导向量(切向量)、梯度向量和方向导数的几何含义:\\ 假设曲线T在三维空间中的参数方程为: \begin{cases} x=t \\ y=2t \\ z=-t^2+4 \end{cases} \\ 则曲线T的向量值函数为f(t)=t\cdot i+2t\cdot j+(-t^2+4)\cdot k,导向量f'(t_0)=i+2j+(-2t_0)\cdot k \\ 令t_0=1且\Delta t<0,则点M坐标为(1,2,3),且M点导向量f'(t_0)=f'(1)=-i-2j+2k \\ \,\\ 如图1所示,为曲线T的大致图形。该曲线始终在y=2x平面内,投影也始终在y=2x这条直线上 \\ 而下面讲的方向导数和梯度向量和这个没关系,方向导数与梯度向量是对于曲面而言的,\\ 梯度向量的表达式含有偏导数,而偏导数和向量值函数的分量函数的导数意义是不同的,\\ 比如f_x(x_0,y_0)与上面的x'就不同,f_x(x_0,y_0)是z对x的偏导数,而x'是x对t的导数,\\ 并且梯度向量的大小、方向与向量(x',y')的大小、方向都不同 \\ \,\\ 下面再介绍梯度向量的几何意义 \\ 其实际上就是曲面上某一点的切面的法向量在xOy平面上的投影,如图2所示\\ 因为垂直于法线投影的的方向会将曲面切割为一个等值线,因此方向导数为0,而垂直的话肯定就最大了因为等值线一直在最大限度的变化 \\ 前面介绍过曲面切面的法向量为(F_x,F_y,F_z),而梯度向量为(\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}),F_x等于\frac{\partial z}{\partial x}吗,下面来证明一下 \\ 为了证实普遍性,创造一个复杂点的函数x^2+3y+xz=0,\\ 求得F_x=\frac{x^2-3y}{x},F_y=3,\frac{\partial z}{\partial x}=\frac{3y-x^2}{x^2},\frac{\partial z}{\partial y}=-\frac{3}{x} \\ \frac{F_x}{F_y}=\frac{\partial z}{\partial x}/\frac{\partial z}{\partial y},因此成立 \\ 梯度的模=该梯度方向的方向导数,即\sqrt{f_x^2+f_y^2}=f_x\cos\alpha+f_y\cos\beta
定理:如果函数f(x,y)在点P0(x0,y0)可微分,那么函数在该点沿任一方向l的方向导数都存在且有∂l∂f∣(x0,y0)=fx(x0,y0)cosα+fy(x0,y0)cosβ,α和β是方向l的方向角梯度向量:gradf(x0,y0)=∇f(x0,y0)=fx(x0,y0)i+fy(x0,y0)j∇=∂x∂i+∂y∂j称为二维的向量微分算子或Nabla算子∂l∂f∣(x0,y0)=fx(x0,y0)cosα+fy(x0,y0)cosβ=gradf(x0,y0)⋅el=∣gradf(x0,y0)∣cosθθ是梯度向量与方向l的夹角,因此由如下几种特殊情况:⎩
⎨
⎧θ=0,方向导数最大,表明函数在某点的方向导数最大的方向是与梯度向量同向的方向θ=π,是函数在该点的方向导数最小的方向,在该方向函数值减小最快θ=2π,函数在该点的方向导数为0,即函数值在该方向没有变化导向量(切向量)、梯度向量和方向导数的几何含义:假设曲线T在三维空间中的参数方程为:⎩
⎨
⎧x=ty=2tz=−t2+4则曲线T的向量值函数为f(t)=t⋅i+2t⋅j+(−t2+4)⋅k,导向量f′(t0)=i+2j+(−2t0)⋅k令t0=1且Δt<0,则点M坐标为(1,2,3),且M点导向量f′(t0)=f′(1)=−i−2j+2k如图1所示,为曲线T的大致图形。该曲线始终在y=2x平面内,投影也始终在y=2x这条直线上而下面讲的方向导数和梯度向量和这个没关系,方向导数与梯度向量是对于曲面而言的,梯度向量的表达式含有偏导数,而偏导数和向量值函数的分量函数的导数意义是不同的,比如fx(x0,y0)与上面的x′就不同,fx(x0,y0)是z对x的偏导数,而x′是x对t的导数,并且梯度向量的大小、方向与向量(x′,y′)的大小、方向都不同下面再介绍梯度向量的几何意义其实际上就是曲面上某一点的切面的法向量在xOy平面上的投影,如图2所示因为垂直于法线投影的的方向会将曲面切割为一个等值线,因此方向导数为0,而垂直的话肯定就最大了因为等值线一直在最大限度的变化前面介绍过曲面切面的法向量为(Fx,Fy,Fz),而梯度向量为(∂x∂z,∂y∂z),Fx等于∂x∂z吗,下面来证明一下为了证实普遍性,创造一个复杂点的函数x2+3y+xz=0,求得Fx=xx2−3y,Fy=3,∂x∂z=x23y−x2,∂y∂z=−x3FyFx=∂x∂z/∂y∂z,因此成立梯度的模=该梯度方向的方向导数,即fx2+fy2=fxcosα+fycosβ
【图1】
【图2】
多元函数的极值及其求法
如果是极值点,则各偏导数为 0 如何判断是不是极值点: { 1 、解方程组 f x = 0 , f y = 0 ,求得一些驻点(驻点不一定是极值点) 2 、对每一个驻点,求出二阶偏导数的值 A ( f x x )、 B ( f x y )、 C ( f y y ) 3 、 A C − B 2 > 0 有极值,且 A < 0 有极大值, A > 0 有极小值 4 、 A C − B 2 < 0 没有极值 5 、 A C − B 2 = 0 另作讨论 偏导数不存在的点也有可能是极值点,如 z = − x 2 + y 2 在 ( 0 , 0 ) 点偏导数不存在,但却是极大值点 条件极值求法: 1 、化为无条件极值; 2 、拉格朗日乘数法 拉格朗日乘法数求解步骤: { 1 、先作拉格朗日函数 L ( x , y ) = f ( x , y ) + λ φ ( x , y ) 2 、求其偏导数,联立方程组: { f x + λ φ x = 0 f y + λ φ y = 0 φ ( x , y ) = 0 3 、解出 x 、 y 、 λ , ( x , y ) 就是可能的条件极值点 如果是极值点,则各偏导数为0 \\ 如何判断是不是极值点:\\ \begin{cases} 1、解方程组f_x=0,f_y=0,求得一些驻点(驻点不一定是极值点)\\ 2、对每一个驻点,求出二阶偏导数的值A(f_{xx})、B(f_{xy})、C(f_{yy})\\ 3、AC-B^2>0有极值,且A<0有极大值,A>0有极小值 \\ 4、AC-B^2<0没有极值 \\ 5、AC-B^2=0另作讨论 \end{cases} \\ 偏导数不存在的点也有可能是极值点,如z=-\sqrt{x^2+y^2}在(0,0)点偏导数不存在,但却是极大值点 \\ \,\\ 条件极值求法:1、化为无条件极值;2、拉格朗日乘数法 \\ 拉格朗日乘法数求解步骤:\\ \begin{cases} 1、先作拉格朗日函数L(x,y)=f(x,y)+\lambda \varphi(x,y) \\ 2、求其偏导数,联立方程组: \begin{cases} f_x+\lambda \varphi_x=0 \\ f_y+\lambda \varphi_y=0 \\ \varphi(x,y)=0 \end{cases} \\ 3、解出x、y、\lambda,(x,y)就是可能的条件极值点 \end{cases} 如果是极值点,则各偏导数为0如何判断是不是极值点:⎩ ⎨ ⎧1、解方程组fx=0,fy=0,求得一些驻点(驻点不一定是极值点)2、对每一个驻点,求出二阶偏导数的值A(fxx)、B(fxy)、C(fyy)3、AC−B2>0有极值,且A<0有极大值,A>0有极小值4、AC−B2<0没有极值5、AC−B2=0另作讨论偏导数不存在的点也有可能是极值点,如z=−x2+y2在(0,0)点偏导数不存在,但却是极大值点条件极值求法:1、化为无条件极值;2、拉格朗日乘数法拉格朗日乘法数求解步骤:⎩ ⎨ ⎧1、先作拉格朗日函数L(x,y)=f(x,y)+λφ(x,y)2、求其偏导数,联立方程组:⎩ ⎨ ⎧fx+λφx=0fy+λφy=0φ(x,y)=03、解出x、y、λ,(x,y)就是可能的条件极值点