1、简介

1.1 假设检验的定义

• 什么是假设检验？
  统计学有两个推断统计方法，一个是参数估计，另一个是假设检验。

• 参数估计用样本统计量来推断总体参数的方法
  假设检验是基于某一假设的前提下，同样利用样本统计量去检验这个假设是否成立。

1.2 假设检验的基本步骤

假设检验是一种统计推断方法，用于判断一个统计样本中的观察结果是否与预期的理论分布相符。下面是假设检验的基本步骤：

• （1）建立原假设（H0）和备择假设（H1）：原假设（H0）是我们想要进行假设检验的观察结果的预期结果。 备择假设（H1）是与原假设相反的假设，即观察结果与预期结果不符。

• （2）选择合适的统计检验方法：根据问题的性质和数据类型，选择适当的统计检验方法。例如，t检验适用于比较样本均值，卡方检验适用于比较分类变量等。

• （3）收集和整理数据：收集和整理与问题相关的样本数据，确保数据的质量和完整性。

• （4）计算统计量：使用所选择的统计检验方法，计算适当的统计量。例如，t检验中的t值，卡方检验中的卡方值等。

• （5）获取p值：根据计算的统计量和观察样本数据，计算得到一个p值（或显著性水平）。p值表示给定观察结果出现的概率，如果p值小于预设的显著性水平（通常为0.05），则拒绝原假设。

• （6）进行假设判断：根据得到的p值和预设显著性水平，做出假设判断：
  如果p值小于显著性水平，拒绝原假设，接受备择假设，认为观察结果与预期结果不一致。
  如果p值大于或等于显著性水平，接受原假设，认为观察结果与预期结果一致。

• （7）解释结果： 根据假设判断的结果，解释分析的结果，得出结论。

2、测试数据

• Toy datasets
  • load_iris(*[, return_X_y, as_frame]): Load and return the iris dataset (classification).
  • load_diabetes(*[, return_X_y, as_frame, scaled]): Load and return the diabetes dataset (regression).
  • load_digits(*[, n_class, return_X_y, as_frame]): Load and return the digits dataset (classification).
  • load_linnerud(*[, return_X_y, as_frame]): Load and return the physical exercise Linnerud dataset.
  • load_wine(*[, return_X_y, as_frame])：Load and return the wine dataset (classification).
  • load_breast_cancer(*[, return_X_y, as_frame])：Load and return the breast cancer wisconsin dataset (classification).
• Real world datasets
• Generated datasets
• Loading other datasets

2.1 鸢尾花（Iris plants dataset）

https://scikit-learn.org/stable/datasets/toy_dataset.html#iris-dataset

Iris数据集在模式识别研究领域应该是最知名的数据集了，有很多文章都用到这个数据集。这个数据集里一共包括150行记录，其中前四列为花萼长度，花萼宽度，花瓣长度，花瓣宽度等4个用于识别鸢尾花的属性，第5列为鸢尾花的类别（包括Setosa，Versicolour，Virginica三类）。也即通过判定花萼长度，花萼宽度，花瓣长度，花瓣宽度的尺寸大小来识别鸢尾花的类别。

# pip install scikit-learn
from sklearn.datasets import load_iris

iris = load_iris()
data = iris.data
target= iris.target
print(data)
print(target)

这里data为训练所需的数据集，target为数据集对应的分类标签，属于监督学习。

from sklearn.datasets import load_iris

iris = load_iris()
data = iris.data
target= iris.target
# print(data)
# print(target)
# print('DESCR: ', iris['DESCR'])
print('data_module: ', iris['data_module'])
print('filename: ', iris['filename'])
print('frame: ', iris['frame'])
print('feature_names: ', iris['feature_names'])
print('target_names: ', iris['target_names'])
print('target: ', iris['target'])

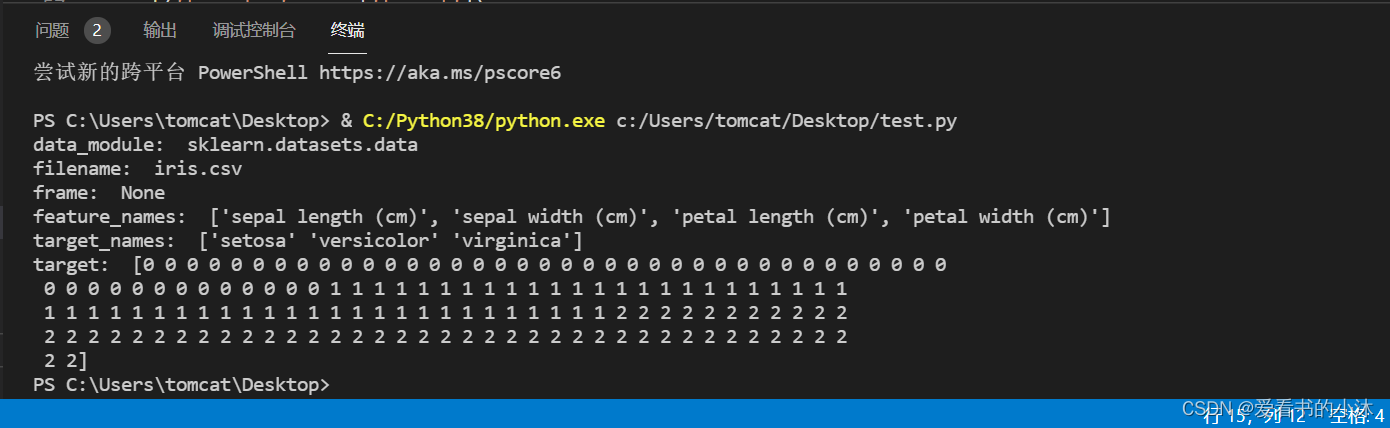
data数据集中的数据一共有4个属性，分别为：

'sepal length (cm)', 
'sepal width (cm)', 
'petal length (cm)', 
'petal width (cm)'

3、正态分布检验

通过样本数据来判断总体是否服从正态分布的检验称为正态性检验。正态分布是很多连续型数据比较分析的大前提，比如t检验、方差分析、相关分析以及线性回归等，均要求数据服从正态分布或近似正态分布。

在统计学中，正态检验主要用于检验一个数据集是否服从正态分布。常用的t检验、方差分析等参数检验都有一个共同的前提条件：样本数据必须服从正态分布，即样本数据必须来源于一个正态分布的总体，若样本数据不服从正态分布，就不能用以上参数检验对数据进行分析，而应该使用非参数检验（如卡方检验、置换检验等）。因此在对数据进行统计分析之前，第一步就需要对数据进行正态性检验，以检验该数据来自正态分布总体的概率有多大，再选择对应的参数或非参数检验方法进行分析。

https://jse.amstat.org/v4n2/datasets.shoemaker.html

3.1 直方图判断

通过直方图初步判断样本数据是否符合正态分布。

# pip install scikit-learn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

# 导入IRIS数据集
iris = load_iris()
iris_data=pd.DataFrame(iris.data,columns=['sepal_length','sepal_width','petal_legth','petal_width'])

fig = plt.figure(figsize = (10,6))
ax2 = fig.add_subplot(1,1,1)
iris_data.hist(bins=50,ax = ax2)
iris_data.plot(kind = 'kde', secondary_y=True,ax = ax2)
plt.grid()
plt.show()

3.2 KS检验（scipy.stats.kstest）

Kolmogorov–Smirnov test (K-S test) 是比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法。以样本数据的累计频数分布与特定的理论分布比较（比如正态分布），如果两者之间差距小，则推论样本分布取自某特定分布。

kstest 是一个很强大的检验模块，除了正态性检验，还能检验 scipy.stats 中的其他数据分布类型，仅适用于连续分布的检验，

原假设：数据符合正态分布
方法：scipy.stats.kstest (rvs, cdf, args = ( ), N = 20, alternative =‘two-sided’, mode =‘approx’)
参数：rvs - 待检验数据，可以是字符串、数组；cdf - 需要设置的检验，这里设置为 norm，也就是正态性检验；alternative - 设置单双尾检验，默认为 two-sided
返回：W - 统计数；p-value - p值

# pip install scikit-learn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from scipy import stats

# 导入IRIS数据集
iris = load_iris()
iris_data=pd.DataFrame(iris.data,columns=['sepal_length','sepal_width','petal_legth','petal_width'])

# data = pd.read_table(r'D:\normal_test\data.txt', encoding='utf-8',names = ['Temperature'])
# df = pd.DataFrame(data, columns =['Temperature'])

u = iris_data['sepal_length'].mean()  # 计算均值
std = iris_data['sepal_length'].std()  # 计算标准差
# 当p值大于0.05，说明待检验的数据符合为正态分布
result = stats.kstest(iris_data['sepal_length'], 'norm', (u, std))
print(result)

KstestResult(statistic=0.08865361377316228, pvalue=0.17813737848592026, statistic_location=5.1, statistic_sign=1)

从输出结果来看pvalue为0.17813737848592026，大于0.05，因此可以接受体温符合正态分布的假设。

3.3 Shapiro-Wilk test（scipy.stats.shapiro）

W检验

方法：scipy.stats.shapiro(x)
参数：x - 待检验数据
返回：W - 统计数；p-value - p值

# pip install scikit-learn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from scipy import stats

# 导入IRIS数据集
iris = load_iris()
iris_data=pd.DataFrame(iris.data,columns=['sepal_length','sepal_width','petal_legth','petal_width'])

res = stats.shapiro(iris_data['sepal_length'])
print(res)
res = stats.shapiro(iris_data['sepal_width'])
print(res)
res = stats.shapiro(iris_data['petal_legth'])
print(res)
res = stats.shapiro(iris_data['petal_width'])
print(res)

3.4 Anderson-Darling test（scipy.stats.anderson）

该方法是由 scipy.stats.kstest 改进而来的，可以做正态分布、指数分布、Logistic 分布、Gumbel 分布等多种分布检验。默认参数为 norm，即正态性检验。

# pip install scikit-learn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from scipy import stats

# 导入IRIS数据集
iris = load_iris()
iris_data=pd.DataFrame(iris.data,columns=['sepal_length','sepal_width','petal_legth','petal_width'])

res = stats.anderson(iris_data['sepal_length'], dist='norm')
print(res)
res = stats.anderson(iris_data['sepal_width'], dist='norm')
print(res)
res = stats.anderson(iris_data['petal_legth'], dist='norm')
print(res)
res = stats.anderson(iris_data['petal_width'], dist='norm')
print(res)

3.5 D’Agostino and Pearson’s test (scipy.stats.normaltest)

方法：scipy.stats.normaltest (a, axis=0)
normaltest 也是专门做正态性检验的模块，原理是基于数据的skewness和kurtosis

scipy.stats.normaltest(a, axis=0, nan_policy=‘propagate’)

a：待检验的数据

axis：默认为0，表示在0轴上检验，即对数据的每一行做正态性检验，我们可以设置为 axis=None 来对整个数据做检验

nan_policy：当输入的数据中有空值时的处理办法。默认为 ‘propagate’，返回空值；设置为 ‘raise’ 时，抛出错误；设置为 ‘omit’ 时，在计算中忽略空值。

# pip install scikit-learn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from scipy import stats

# 导入IRIS数据集
iris = load_iris()
iris_data=pd.DataFrame(iris.data,columns=['sepal_length','sepal_width','petal_legth','petal_width'])

res = stats.normaltest(iris_data['sepal_length'])
print(res)
res = stats.normaltest(iris_data['sepal_width'])
print(res)
res = stats.normaltest(iris_data['petal_legth'])
print(res)
res = stats.normaltest(iris_data['petal_width'])
print(res)

注：p值大于显著性水平0.05，认为样本数据符合正态分布）

4、假设检验

Python 中的假设检验一般用到 scipy 或 statsmodels 包。

4.1 z 检验

对于大样本数据（样本量 ≥ \geq≥ 30），或者即使是小样本，但是知道其服从正态分布，并且知道总体分布的方差时，需要用 z 检验。在 python 中，由于 scipy 包没有 z 检验，我们只能用 statsmodels 包中的 ztest 函数。

# pip install scikit-learn
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
from scipy import stats
import statsmodels.stats.weightstats as sw

# 导入IRIS数据集
iris = load_iris()
# print(iris.data)
iris_data=pd.DataFrame(iris.data,columns=['sepal_length','sepal_width','petal_legth','petal_width'])
print(iris_data['sepal_width'])

result = sw.ztest(iris_data['sepal_width'], value=1)
print('1: ', result)
result = sw.ztest(iris_data['sepal_width'], value=2)
print('2: ', result)
result = sw.ztest(iris_data['sepal_width'], value=3)
print('3: ', result)
result = sw.ztest(iris_data['sepal_width'], value=4)
print('4: ', result)
result = sw.ztest(iris_data['sepal_width'], value=5)
print('5: ', result)

条件设为该样本的均值3时，从 ztest 的运行结果可以看出，统计量值为 1.6110148544749883，而 p 值是 0.10717648482938881，在置信度 α = 0.05 时，由于 p 值大于 α，接受原假设，认为该样本的均值是 3。

# 若要检测该样本均值是否大于 3，即原假设 H0：μ ≥ 3，备选假设为：μ < 3，则我们需要在代码中增加一个参数 alternative=``smaller”
sw.ztest(arr, value=3, alternative="smaller")

# 检测两个样本的均值是否相等，因为两个样本都是大样本，使用 z 检验
sw.ztest(arr, arr2, value=0)

4.2 t 检验

小样本（样本量小于30个），一般用 t 检验。对于 t 检验，可以根据样本特点，用 scipy 包中的 ttest_1sample（单样本 t检验函数），ttest_ind（两个独立样本的 t 检验），ttest_rel （两个匹配样本的 t 检验）。但这些函数得到都是双侧 t 检验的 p 值。如果是单侧检验，我们还要进行一些换算，得到单侧检验的 p 值。

# pip install scikit-learn
import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
from scipy import stats
import statsmodels.stats.weightstats as sw

# 导入IRIS数据集
iris = load_iris()
# print(iris.data)
iris_data=pd.DataFrame(iris.data,columns=['sepal_length','sepal_width','petal_legth','petal_width'])
print(iris_data['sepal_width'])

result = stats.ttest_1samp(iris_data['sepal_width'], 1)
print('1: ', result)
result = stats.ttest_1samp(iris_data['sepal_width'], 2)
print('2: ', result)
result = stats.ttest_1samp(iris_data['sepal_width'], 3)
print('3: ', result)
result = stats.ttest_1samp(iris_data['sepal_width'], 4)
print('4: ', result)
result = stats.ttest_1samp(iris_data['sepal_width'], 5)
print('5: ', result)

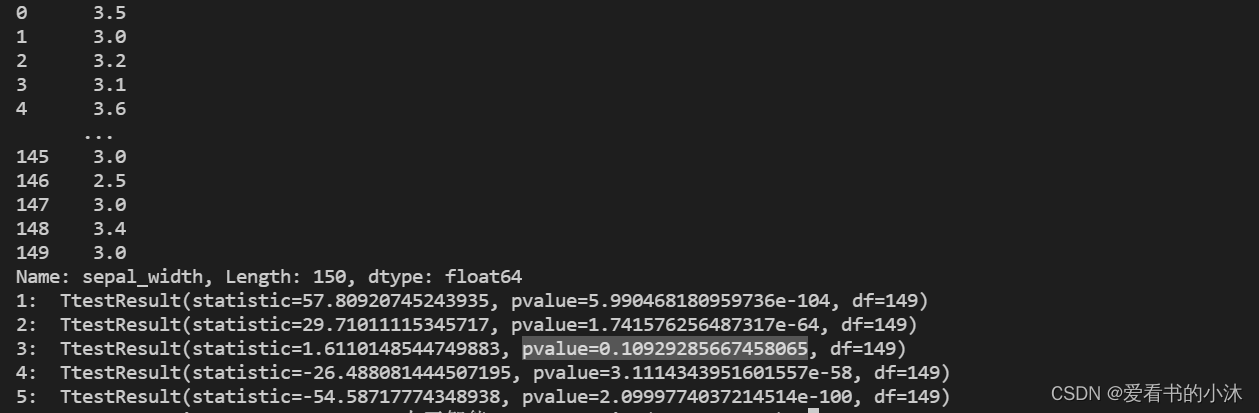
从结果可以看出，双侧检验的 p 值为 0.10929285667458065， 大于置信度 0.05，因此接受原假设，认为样本的均值是3。若是单侧检验中的左侧检验，则 p 值为 0.10929285667458065 / 2 = 0.054646428337290325，若是右侧检验，则 p 值为 1 − 0.10929285667458065 / 2 = 0.9453535716627097。

# 假设两个样本的方差不同，则独立双样本的 t 检验
st.ttest_ind(a, b, equal_var = False)

# 若两个样本是匹配样本，使用函数 ttest_rel
st.ttest_rel(a, b)

# 结果显示，p 值小于置信度 0.05，拒绝原假设，认为这两个匹配样本的均值不同。

结语

如果您觉得该方法或代码有一点点用处，可以给作者点个赞，或打赏杯咖啡；╮(￣▽￣)╭
如果您感觉方法或代码不咋地//(ㄒoㄒ)//，就在评论处留言，作者继续改进；o_O???
如果您需要相关功能的代码定制化开发，可以留言私信作者；(✿◡‿◡)
感谢各位大佬童鞋们的支持！( ´ ▽´ )ﾉ ( ´ ▽´)っ！！！