继承自chapter 3 的自由电子模型：

4.1 单电子近似 One electron approximation

列出电子运动的薛定谔方程：$$E\Psi =-\frac{{\hslash }^2}{2m}{\nabla }^2\Psi +U\Psi$$

根据电子在晶体中运动的实际情况，方程右侧需要包含：电子动能（Kinetic energy of electrons）、离子实动能（Kinetic energy of nuclei）、电子与电子之间作用的势能（Potential energy of electrons）、原子核势能（Potential energy of nuclei
）、电子与原子核之间作用的势能（Interaction between electrons and nuclei
）。因此方程会很冗杂。
在索末菲自由电子模型中，仅考虑电子动能，其他的均不考虑。

单电子近似：电子在离子实势场和其他电子的平均势场中运动。

• 绝热近似 Adiabatic approximation：$m_e\ll m_p,v_e\gg v_p$所有离子实静止不动，把电子系统和离子实系统分开考虑。
• 平均场近似 Mean field approximation：不去讨论原子核的势能和动能，仅考虑电子与电子的作用、电子与离子实的作用。将其他电子的势场等效为一个平均势场。这样研究的电子的势能仅与这个电子的位置有关。

经过单电子近似，多体问题简化为简单的薛定谔方程求解问题：$$[-\sum _i\frac{{\hslash }^2}{2m}{\nabla }_i^2+V(\vec{r})]\psi =E\psi$$

4.2 布洛赫定理与能带基本性质 Bloch theorem and Energy bands

Bloch Theorem 给出了周期性势场中电子的波函数的一般形式。

$$\left(-\frac{{\hslash }^2}{2m}\frac{d^2}{d{x}^2}+U(x)\right)ps{i}_k(x)=E_k{\psi }_k(x)$$

A periodic potential with the period of a: $$U(x)=U(x+na)$$

Bloch’s Theorem - For a particle moving in a periodic potential with the period a, the solution of the Schrodinger equation for this particle must be of a special form:
$${\psi }_k(x)=e^{ikx}\cdot u_k(x)$$

其中，$e^{ikx}$是自由电子平面波，$u_k(x)$是具有晶格周期性的函数$u_k(x)=u_k(x+na)$。

$$|\psi (x+na){|}^2=|\psi (x){|}^2$$

3D: electron in a crystal: $${\psi }_{\mathbf{k}}(\mathbf{r})=e^{i\mathbf{k}\cdot \mathbf{r}}\cdot u_{\mathbf{k}}(\mathbf{r})$$

4.3 克罗尼格-盘纳模型 Kronig-Penney Model

PPT: ENE 311. Lecture 5. The band theory of solids. Band theories help explain the properties of materials. There are three popular models for band theory: - Kronig-Penney model - Ziman model - Feynman model. Kronig-Penney Model.

4.3.1 Schrodinger Equation

将周期性势场简化为周期性有限深方势阱：

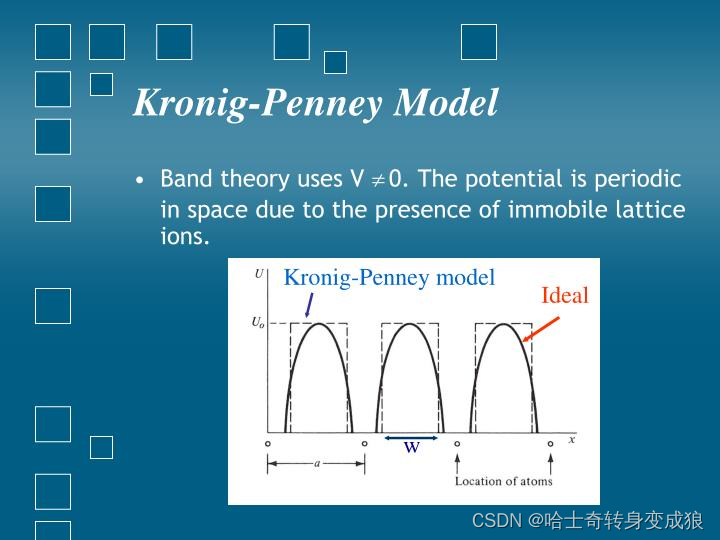
求解薛定谔方程：
$$\left(-\frac{{\hslash }^2}{2m}\frac{d^2}{d{x}^2}+U(x)\right)ps{i}_k(x)=E_k{\psi }_k(x)$$

$$U=\{\begin{array}{ll}0,& region1\\ U_0,region2& \end{array}$$

对解$u_1,u_2$及其波函数进一步分析（边界连续且有周期），得到关于P的方程：

其中，$m$为电子质量，$V_0$为势阱高度，$a$为晶格常数，$w$为势阱宽度。

P越大，原子核对电子束缚能力越强。

4.3.2 The formation of energy bands and P value

讨论关于P的方程：$$P\frac{\sin (\alpha a)}{\alpha a}+\cos (\alpha a)=\cos (ka)$$

（1）$P=0,U_0=0$

$$\alpha a=ka⟶E=\frac{{\hslash }^2{k}^2}{2m}$$

Continuous energy levels—free electron
固体中的自由电子而不是真空中的，此时自由电子的能量仍然是量子化的。

（2）$P\to \infty$

$$\alpha a=\pm n\pi ⟶E=\frac{{\pi }^2{\hslash }^2}{2m{a}^2}{n}^2$$

Discrete energy levels—electron in an infinite potential well as trapped in an atom
分离的能级，电子被原子紧紧束缚

（3）$P\ne 0,\infty$

$$f(\alpha a)=P\frac{\sin (\alpha a)}{\alpha a}+\cos (\alpha a)=\cos (ka)$$

$$\therefore -1\le f(\alpha a)\le 1$$

$${\alpha }^2=\frac{2mE}{{\hslash }^2}$$

The allowed values of the α are limited in the ranges for which $f(\alpha a)$ lies between ±1.

能量受到限制——能带

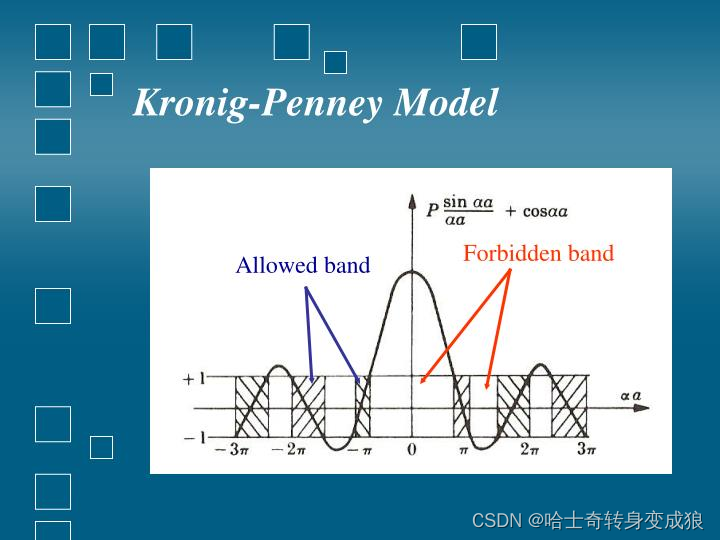
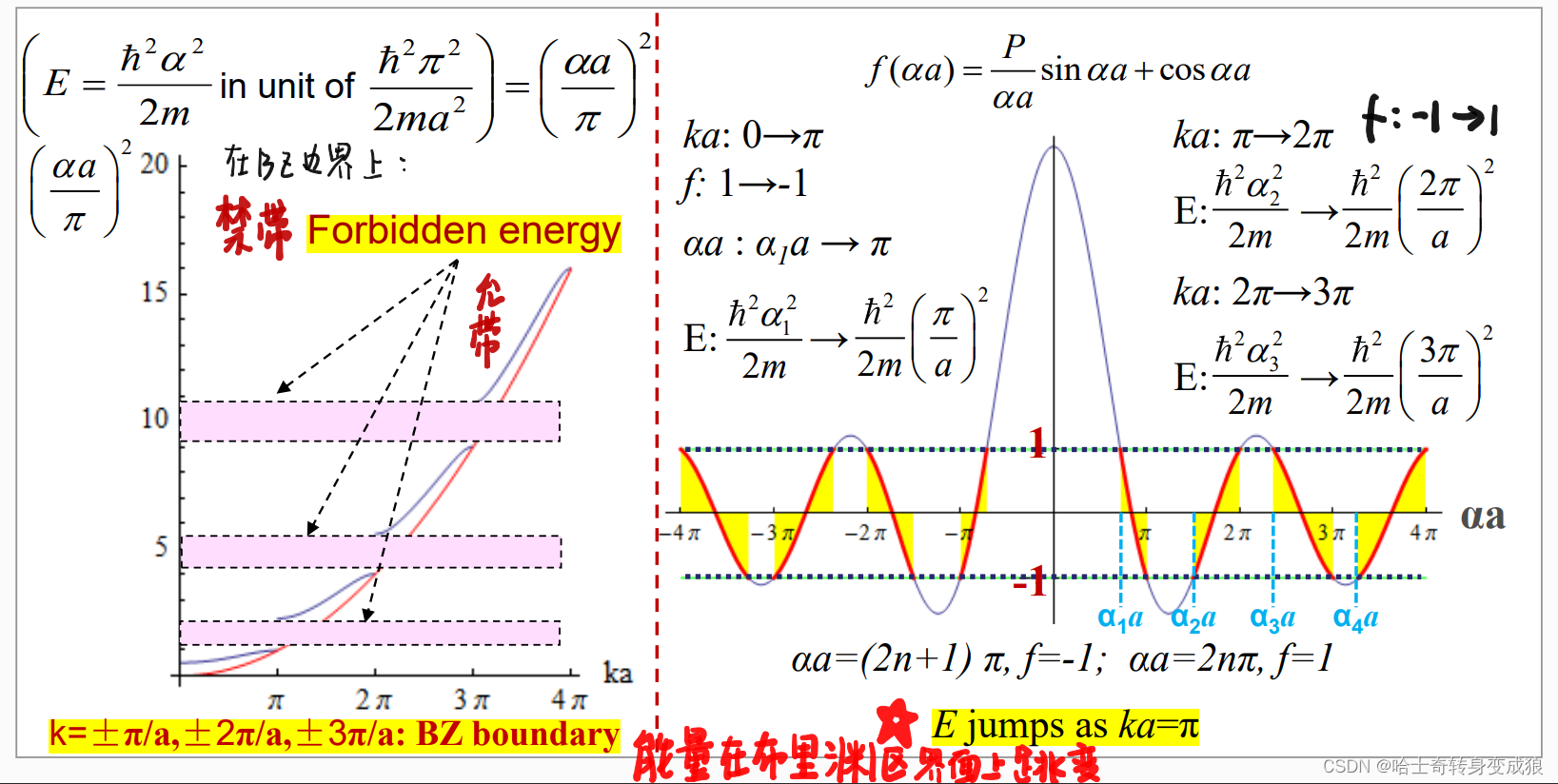
能量在布里渊区界面上发生跳变。

能带具有偶函数特性：

$$E_n(\mathbf{k})=E_n(-\mathbf{k})$$

能带在倒易空间（波矢空间）中具有周期性：

$$E_n(\mathbf{k}+\mathbf{G})=E_n(\mathbf{k})$$

因此可以只在第一布里渊区内研究能带特性：

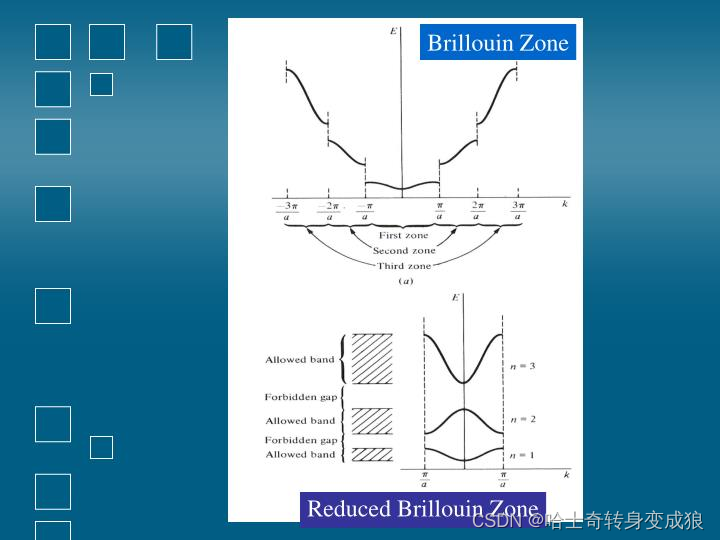
$P\uparrow ,U_{0}w\uparrow$, energy band narrows and gap widens

P反映了原子对电子的束缚能力，P越大，电子受到的限制越大。

4.3.3 Number of k in a band

Number of allowed k in a BZ or in an energy band = Number of primitive cells

能带内的波矢数量 = 原胞数

number of energy state in an energy band: $$\Delta m=\frac{L}{2\pi }\Delta k$$

$L=Na$ N：原胞数；a：晶格常数。

Maximum of 2N electrons in an energy band.

晶体中的原胞数量N往往非常大，所有每个能级中喊有非常多的量子态，能级之间非常接近，可以称之为“准连续”。在能带中能量实际上也是量子化的（分立的），但是由于准连续，可以视为“带”。

4.4 近自由电子近似 Nearly Free Electron Model

金属等晶体中的电子是在一个很弱的周期势场中运动，其运动特性如同自由电子，可以近似为自由电子。在晶体中，电子在远离原子核的位置受到的势场是稳恒不变的，在很靠近原子的位置势场很大且变化剧烈。总的来说，电子在晶格中的运动可以视为平面波在周期性结构中的传播。

PPT：能带理论与布洛赫定理

4.4.1 Energy gap

布拉格反射导致带隙。
Bragg reflection → energy band splitting → energy gap

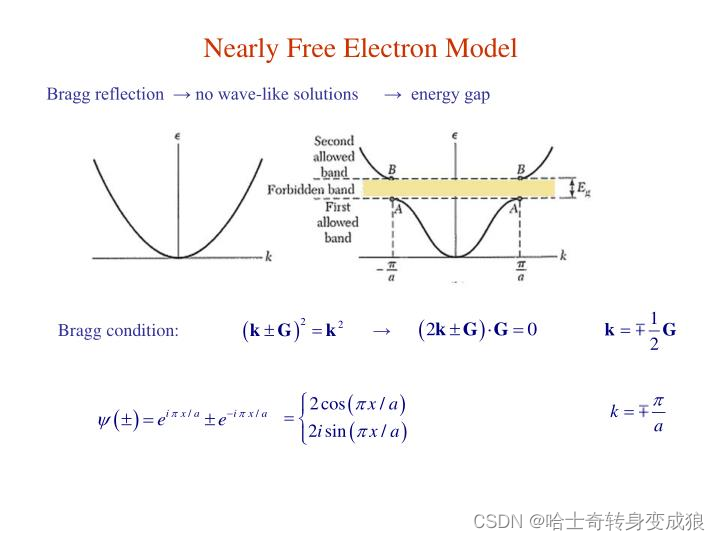
（1）远离布里渊区界面：电子波（平面波）自由地通过晶体。

不发生布拉格反射，能量近似于自由电子。

$$\psi (x)=e^{ikx},E=\frac{{\hslash }^2{k}^2}{2m}$$

（2）靠近布里渊区界面：在界面发生反射，反射波与入射波相互作用，能量分裂成能隙，电子准连续谱分割。

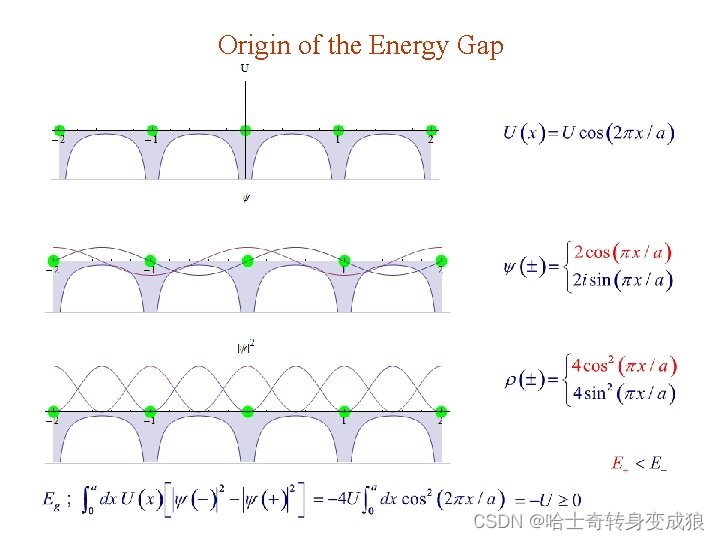
Bragg Reflection leads the two possible combinations of the right and the left going waves：

$\psi (\pm )$代表两种驻波（traveling wave），即电子在空间中分布的两种状态；
$\rho (+)$代表电子更多地分布在靠近离子实的位置，对应于$\psi (+)$，具有更低的能量，Standing wave with high density at atom position.
$\rho (-)$代表电子更多地分布远离离子实的位置，对应于$\psi (-)$，具有更高的能量，Standing wave with low density at atom position.

The gap is equal to two times of the Fourier component of the crystal potential. The stronger the modulation of the potential, the larger the gaps.

$$\Delta E=E_{+}-E_{-}=2|U_n|$$

$$U(x)=U(x+a)=U_0+\sum _{n\ne 0}{U}_n{e}^{i\frac{2pinx}{a}}$$

$$U_0=\frac{1}{L}in{t}_0^{L}U(x)dx,U_n=\frac{1}{L}{\int }_0^{L}U(x)exp\left(-i\frac{2\pi nx}{a}\right)dx$$

4.4.2 Constructing energy bands

一维原子链里的近自由电子的能带等同于自由电子时的能量，但是也有能带（能量量子化）。

利用周期性平移，可以将能带曲线移到第一布里渊区，从而仅在1-BZ中研究。

注意：电子可能沿着不同的方向去运动，比如正空间中晶面簇的法线方向、倒空间中倒格矢的方向。**不同方向上的能带关系组合在一起，构成了真实晶体的能带图。**波矢落在布里渊区界面上也有不同的落法，能带之间存在交叠，所以需要找到真正的带隙，如下图所示：


How to construct energy bands in a 3D crystal?

1D: $$E=\frac{{\hslash }^2}{2m}(k-G{)}^2$$

3D: $$E=\frac{{\hslash }^2}{2m}[(k_x-G_x{)}^2+(k_y-G_y{)}^2+(k_z-G_z{)}^2]$$

不同的G对应于不同的能带：不同的G代表了不同的晶面间距，事实上G可以用(h,k,l)的组合来表示，进而反映了电子受到的周期性势场的不同，从而代表了不同的能带。

空晶格近似：将布里渊区界面上连续的E(k)打开，使能级分裂产生能隙，可以看到能隙交叠得到实际意义上的能隙，进而得到实际的晶格能带结构。

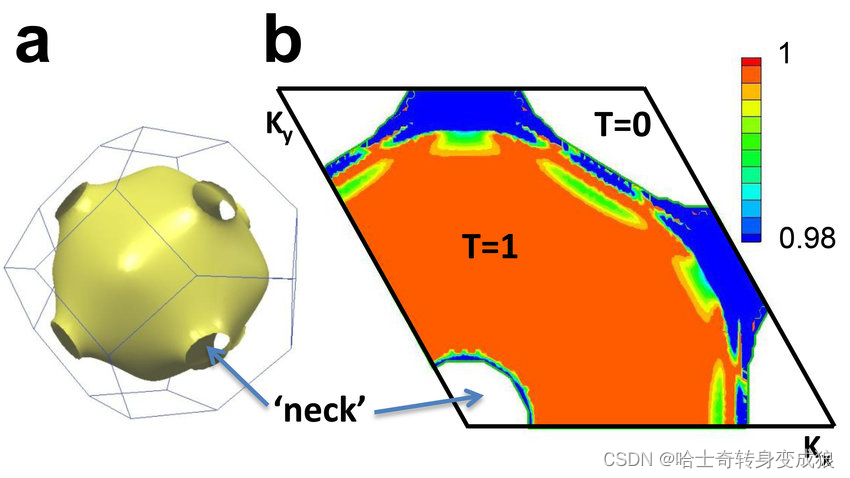
4.4.3 Fermi Surface

Summary: The Fermi Surface for Nearly Free Electrons

1. The interaction of the electron with the periodic potential of the crystal cause energy gaps at the zone boundaries. 电子与周期性势场的相互作用导致布里渊区界面处产生能隙。
2. Almost always the Fermi surface will intersect zone boundaries perpendicularly. 费米面几乎总是和布里渊区界面垂直。
3. The crystal potential will round out sharp corners in the Fermi surfaces. 晶体电势将使得费米面的尖角更加圆滑。
4. The total volume enclosed by the Fermi surface depends only on the electron concentration and is independent of the details of the lattice interaction. 费米面包围的总体积仅与（价）电子浓度有关，与晶格相互作用的细节无关。

不考虑周期性势场，费米面仍然是球面的，但是考虑周期性势场，电子波矢落在布里渊区界面上会发生强烈的布拉格反射，会产生禁带，从而不再是球面。

4.5 紧束缚近似 Tight-binding Approximation

4.5.1 原子轨道线性组合 Linear Combination of Atomic Orbitals

由布洛赫提出的LCAO原子轨道线性组合理论，原子和原子之间的作用比较微弱，可以把最邻近原子的势场看作零级近似，把其他原子的势场看作微扰。

原子轨道线性组合可以解释半导体、绝缘体原子的能带，也可以在一定程度上解释金属原子内层电子的行为，对过渡金属3d能带的解释尤其有效。

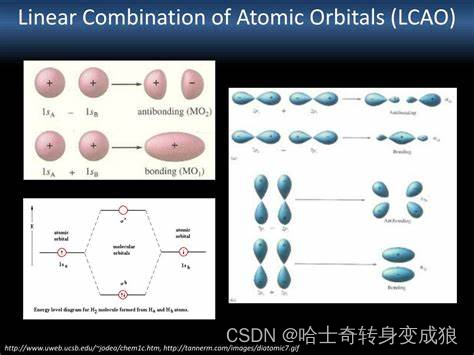
Wave function of electron surrounding atom l：$\psi (r)$

基波函数由原子轨道波函数线性组合而成，同时考虑布洛赫定理。
$$\psi (\mathbf{r})=\sum _l{C}_l{\psi }_j(\mathbf{r}-{\mathbf{R}}_l),{\psi }_k(\mathbf{r})=C{e}^{i\mathbf{k}\cdot \mathbf{r}}{u}_k(\mathbf{r})$$

对薛定谔方程中的势场进行微扰论研究：
$$U(\mathbf{r})=V({\mathbf{r}-\mathbf{R}}_l)+[U(\mathbf{r})-V({\mathbf{r}-\mathbf{R}}_l)]=V({\mathbf{r}-\mathbf{R}}_l)+\Delta V({\mathbf{r}-\mathbf{R}}_l)$$

其中：$V({\mathbf{r}-\mathbf{R}}_l)$是原子l的势能，是零级近似；$\Delta V({\mathbf{r}-\mathbf{R}}_l)$是其他原子势场的扰动。

通过复杂的求解过程，可以得到：
$$E(\mathbf{k})=E_s-\beta -\sum _{(n,n)}{e}^{i{\mathbf{k}\cdot \mathbf{R}}_m}\gamma ({\mathbf{R}}_m)$$

其中：
$E_s$是电子在孤立原子中的能量，zeroth approximation of E(k)；
$\beta$是一个常数 – integration of crystal field；
$\gamma ({\mathbf{R}}_m)$：相互作用的积分，integration of interacting；
最后一项求和是对格点${\vec{R}}_m$的最近邻原子求和

4.5.2 Physical Image

$$E(\mathbf{k})=E_s-\beta -\sum _{(n,n)}{e}^{i{\mathbf{k}\cdot \mathbf{R}}_m}\gamma ({\mathbf{R}}_m)$$

1. 一个电子在晶体中的能量与这个电子在孤立原子中的能量只相差一个常数和一个与波矢$\vec{k}$有关的量。
2. 这个与波矢$\vec{k}$有关的量使得原子份力的能级转化为固体的能带。
3. $E(\mathbf{k})$是关于波矢$\vec{k}$的周期函数。
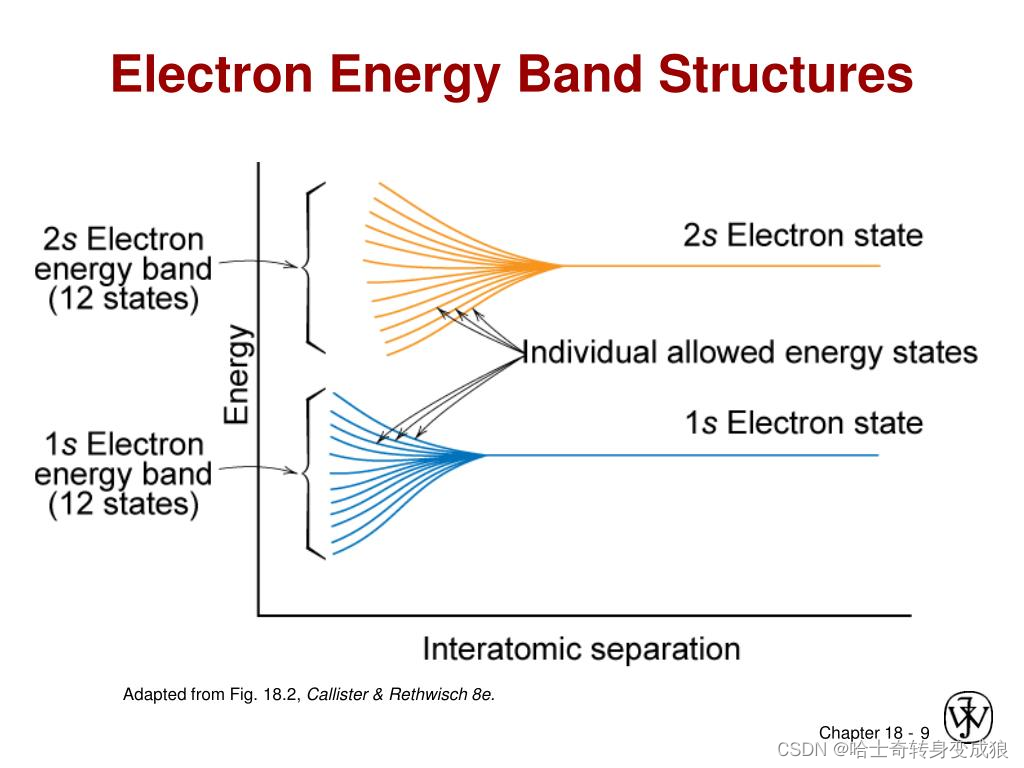
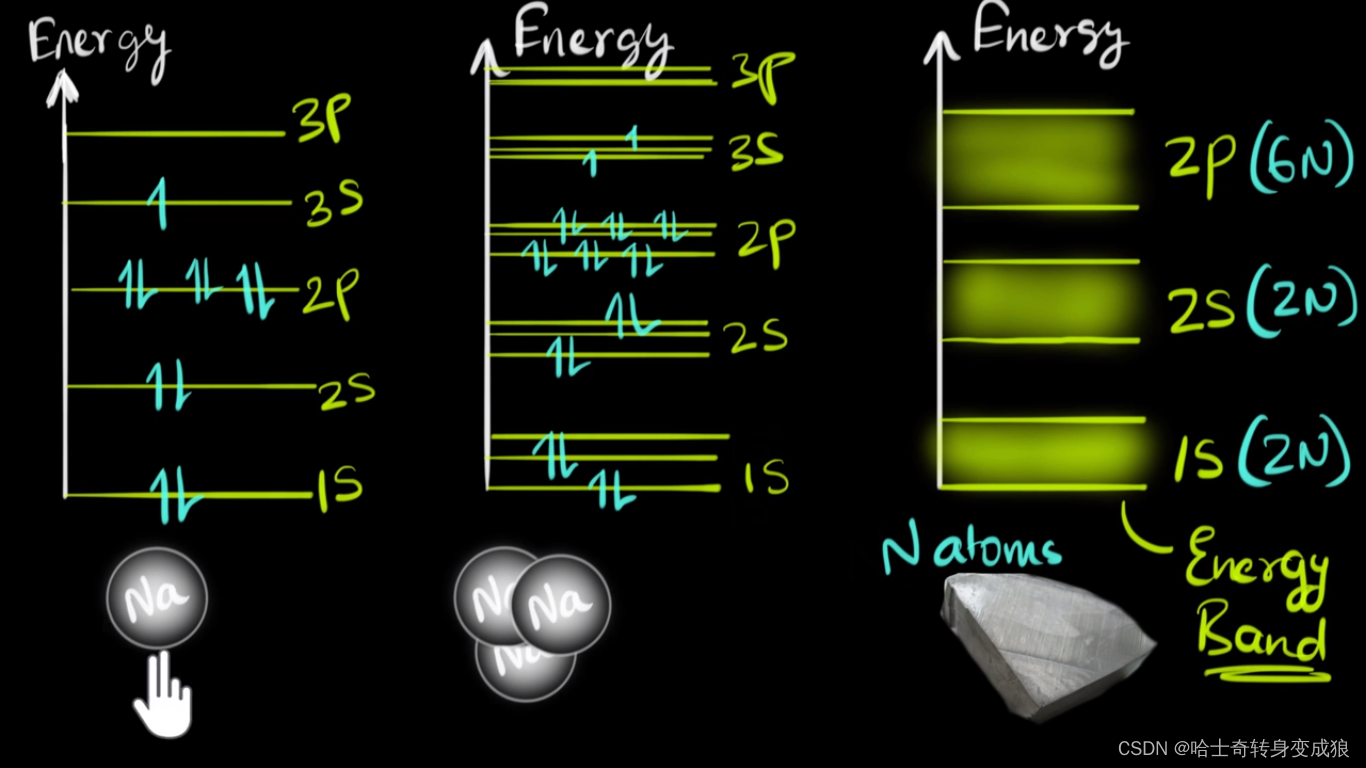
4. 有N个原子相互作用，则代表有N个能级分裂出来，它们是准连续的，所以形成能带。

如下图所示，简并的1s能态分裂成量子化的能带。

4.5.3 Conductor, semiconductor, insulator

（1）金属、半导体、绝缘体的能带差异

• 奇数个价电子，如果存在半满能带——导体；
• 偶数个价电子，如果满带和它上面的空带有交叠，也能具有良好的导电性；
  比如Mg价电子为2，3s满带，但是3s和3p交叠，可以填充8N个电子，所以价电子为2时尚未填满，仍有空余量子态来填充电子；
• 半导体的禁带宽度比较小；
• 绝缘体的禁带宽度很大；
• 满带被电子完全填充，没有空的量子态对外加势场（电场）作响应；
• 一般来说，只有不满或者半满的带才导电。

（2）第IV主族元素的能带结构

当原子之间的间距逐渐减小的时候，孤立能级展宽成能带，s、p能带合成为一个能带，此时该能带上具有8N个量子态；原子间距进一步减小，能带再一次分裂，产生能隙$E_g$，分裂出的能带各自含有4N个量子态，随着原子间距的进一步缩小，能带逐渐远离，能隙增大；到达平衡位置$a_0$之后，原子之间呈现出排斥作用。

4.6 总结：如何用近自由电子近似和紧束缚模型来逐渐逼近真实的电子运动情况

4.6 电子的准经典运动 Motion of Electron

4.6.1 群速度与相速度 group velocity

• 相速度 phase velocity $v_{\varphi }=\frac{\lambda }{T}=\frac{\omega \lambda }{2\pi }=\frac{\omega }{k}$
• 群速度 group velocity $v_k=\frac{d\omega }{dk}$

相速度是波的速度，群速度是包络的速度。

$$v_k=\frac{d\omega }{dk}=\frac{dE}{dp}=\frac{d\left(\frac{p^2}{2m}\right)}{dp}=\frac{2p}{2m}=v_{particle}$$

即：群速度等于粒子速度。$v_k=v_{particle}$

4.6.2 有效质量 effective mass

电子运动受到外加电场和周期性势场的共同作用。
$$m\frac{dv}{dt}=F_{ϵ}+F_{crystalpotential}$$
当我们用经典力学的理论研究外加电场对电子运动的作用时，可以将周期性势场的作用融合进粒子质量，即将粒子质量重新定义为“有效速度”。
$$m^{\ast }\frac{dv}{dt}=F_{ϵ}$$

$$m^{\ast }=\frac{{\hslash }^2}{\frac{d^{2}E}{d{k}^2}}$$

When an electric field ε acts on a free electron, it exerts a force eε that, from Newton’s law, will produce an acceleration inversely proportional to its mass, $a=\frac{eϵ}{m}$. What happens when the electron to be accelerated is not free but happens to be in a crystal under the influence of the potential of the lattice ions? The answer is that it will still accelerate according to Newton’s law; however, the electron responds as if it had some effective mass $m^{\ast }$, which is different from its true mass. As we will show, this is because $ϵ$ is not the only electric field acting on the electron inside the crystal.
We will introduce this concept by using a semi-classical picture: an argument that is half classical and half quantum mechanical. The quantum mechanical part lies in the fact that the motion of an electron is governed by a wave, and that the velocity of the electron is equal to the group velocity vgroup of the wave, that is, the velocity of the envelope, of the wave packet.

如何求解有效质量？

关键：E(k)

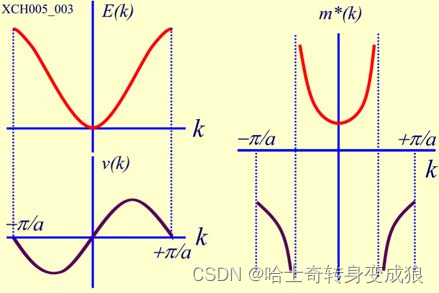
• 靠近能带底：k~0，远离布拉格条件，没有反射，与自由电子近似，外加电场作用使之加速，有效质量大于0；
• 靠近能带顶：k~$\frac{n\pi }{d}$，布拉格反射极其强烈且与外加电场作用相反，可以超过外电场加速作用，有效质量小于0
• 在能带中间的某一个确定的k值：布拉格反射抵消外电场作用，表现为对外加电场不响应，有效质量趋于无穷大。

4.6.3 空穴 hole