1 引言

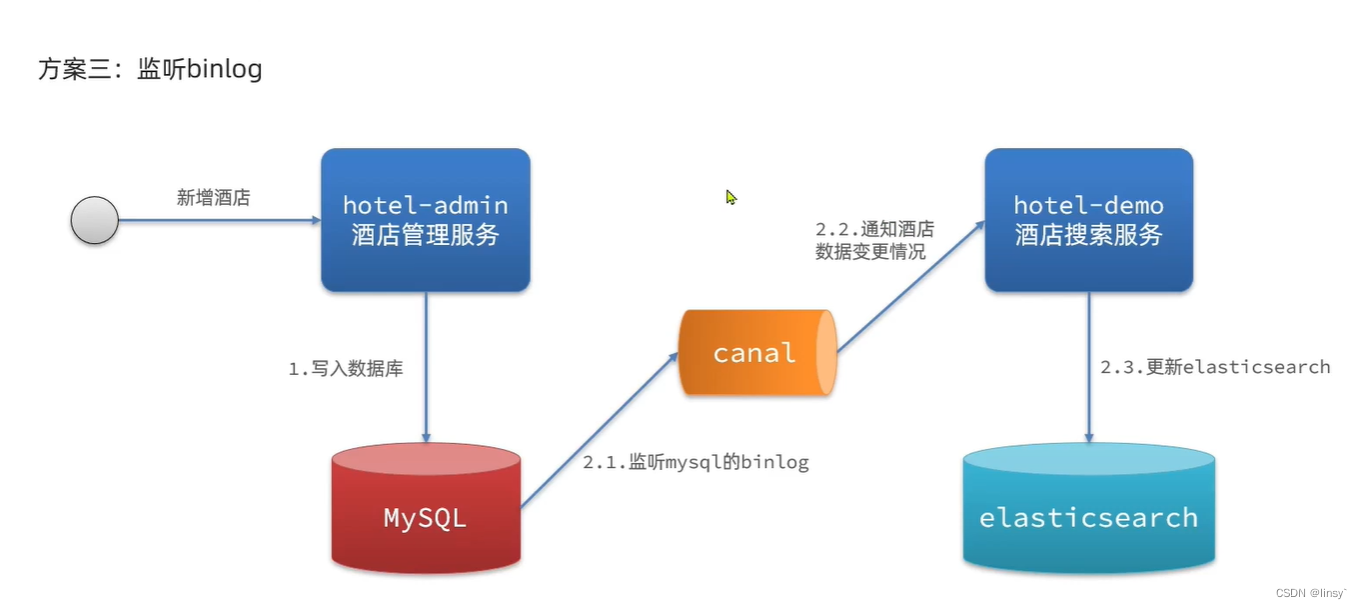
在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、Swish、ELU、SELU、GELU、Softmax、Softplus、Mish、Maxout、HardSigmoid、HardTanh、Hardswish、HardShrink、SoftShrink、TanhShrink、RReLU、CELU、ReLU6、GLU、SwiGLU、GTU、Bilinear、ReGLU、GEGLU、Softmin、Softmax2d、Logsoftmax、Identity、LogSigmoid、Bent Identity、Absolute、Bipolar、Bipolar Sigmoid、Sinusoid、Cosine、Arcsinh、Arccosh、Arctanh)。在这篇文章中，会接着上文提到的众多激活函数继续进行介绍，给大家带来更多不常见的激活函数的介绍。这里放一张激活函数的机理图：

最后，对于文章中没有提及到的激活函数，大家可以通过评论指出，作者会在后续的文章中进行添加补充。

2 激活函数

2.1 LeCun Tanh激活函数

论文链接：LeCun, Yann A., Léon Bottou, Genevieve B. Orr, and Klaus-Robert Müller. “Efficient backprop.” In Neural networks: Tricks of the trade, pp. 9-48. Springer, Berlin, Heidelberg, 2012.

LeCun Tanh 激活函数是双曲正切函数（tanh）的缩放和平移版本一种双曲正切函数（tanh）的变种，由深度学习领域的著名科学家Yann LeCun提出。这个变种的目标是改善双曲正切函数在某些情况下可能导致的梯度问题。其数学表达式为和数学图像分别如下所示：
$$f(x)=1.7159\ast \tanh (\frac{2}{3}x)$$
这里的 $1.7159$ 和 $\frac{2}{3}$ 都是根据实验和经验选择的。
优点：

• 缓解梯度爆炸问题： LeCun Tanh 函数通过对双曲正切函数进行缩放和平移，将输出范围限制在 [-1.7159, 1.7159]，相比标准双曲正切函数的 [-1, 1] 范围，有助于缓解梯度爆炸问题，使得训练更加稳定。
• 非线性变换： 与标准双曲正切函数相比，LeCun Tanh 函数在中间区域更接近线性，同时仍保留了非线性的特性。这可能有助于更好地在网络中引入非线性变换，从而提高网络的表达能力。
• 适用于中心化数据： LeCun Tanh 函数在输出的非线性部分具有对称性，适用于均值为零的中心化数据。

缺点：

• 梯度消失问题： 尽管 LeCun Tanh函数通过缩放提高了输出范围，但在函数的两端，即当输入远离零时，仍然存在梯度消失的问题。这可能在深层网络中影响梯度传播和训练。

虽然理论上而言：LeCun Tanh激活函数因其特性会被一些特殊问题应用，但是在当前深度学习模型的背景下很难得到广泛应用。。。

2.2 TanhExp激活函数

论文链接：Liu, Xinyu, and Xiaoguang Di. “TanhExp: A smooth activation function with high convergence speed for lightweight neural networks.” IET Computer Vision 15, no. 2 (2021): 136-150.

TanhExp激活函数是一种用于轻量级神经网络的具有高收敛速度的平滑激活函数，在不增加网络规模的情况下，只需要少量的训练周期和不增加额外参数，TanhExp就可以提高轻量级神经网络的容量。TanhExp的数学表达式为和数学图像分别如下所示：
$$f(x)=xtanh(e^x)$$

优点：

• 线性变换：在正部分，一旦输入大于 1，TanhExp 几乎等于线性变换，输出值和输入值的变化不超过0.01。如上所述，ReLU系列都旨在修改负部分，同时保留正部分的初始形式。这是因为线性变换在训练中是合理的，而以前的非分段平滑激活函数忽略了这个属性。
• 加速参数：TanhExp显示出接近零的陡峭梯度，这可以加速网络中参数的更新。它以最小值 -0.3532 为以下边界，上方为无界。负值可能会使激活的平均值接近于零，从而加速学习过程。正部分近似线性，当输入大于0时变化不超过01.1，梯度略大于其他平滑激活函数。这些属性使 TanhExp 能够比同类产品更快地计算和收敛，同时提供更好的结果。
• 鲁棒性好：实验结果显示，当网络更深入时，网络会受到过度拟合的影响，而TanhExp 的精度几乎没有下降。此外，即使添加了噪声和更改数据集，TanhExp 函数仍保持稳定。实验结果如下图所示：
  

缺点：

• 具有一定适用范围：当前作者仅在轻量级网络中进行使用，无法验证深度网络中该激活函数的效果。。。

虽然理论上而言：TanhExp激活函数具有较好的效果，但是在当前深度学习模型的背景下还未得到广泛应用。。。。

3. 总结

到此，使用 激活函数总结（十三） 已经介绍完毕了！！！ 如果有什么疑问欢迎在评论区提出，对于共性问题可能会后续添加到文章介绍中。如果存在没有提及的激活函数也可以在评论区提出，后续会对其进行添加！！！！

如果觉得这篇文章对你有用，记得点赞、收藏并分享给你的小伙伴们哦😄。