目录
用向上调整建堆的时间复杂度
1.向上调整建堆的时间复杂度O(N*logN)
2.数学论证
3.相关代码
用向下调整建堆的时间复杂度
1.建堆的时间复杂度为O(N)
2.数学论证
3.相关代码
完结撒花✿✿ヽ(°▽°)ノ✿✿
博主建议:面试的时候可能会被面试官问到建堆时间复杂度的证明过程,最好背下来,到时候能回答出你就是最靓的仔!!!
注:堆是完全二叉树,但以满二叉树来分析的原因:
- 方便进行数学论证
- 满二叉树是特殊的完全二叉树
- 满二叉树挂的节点最多,与时间复杂度的计算一般是求是求算法的最坏运行情况相符
- 时间复杂度本来看的就是近似值,多几个节点不影响最终结果
用向上调整建堆的时间复杂度
注:一般采用的都是向下调整的方式建堆的,用向上调整建堆比较少
1.向上调整建堆的时间复杂度O(N*logN)
2.数学论证
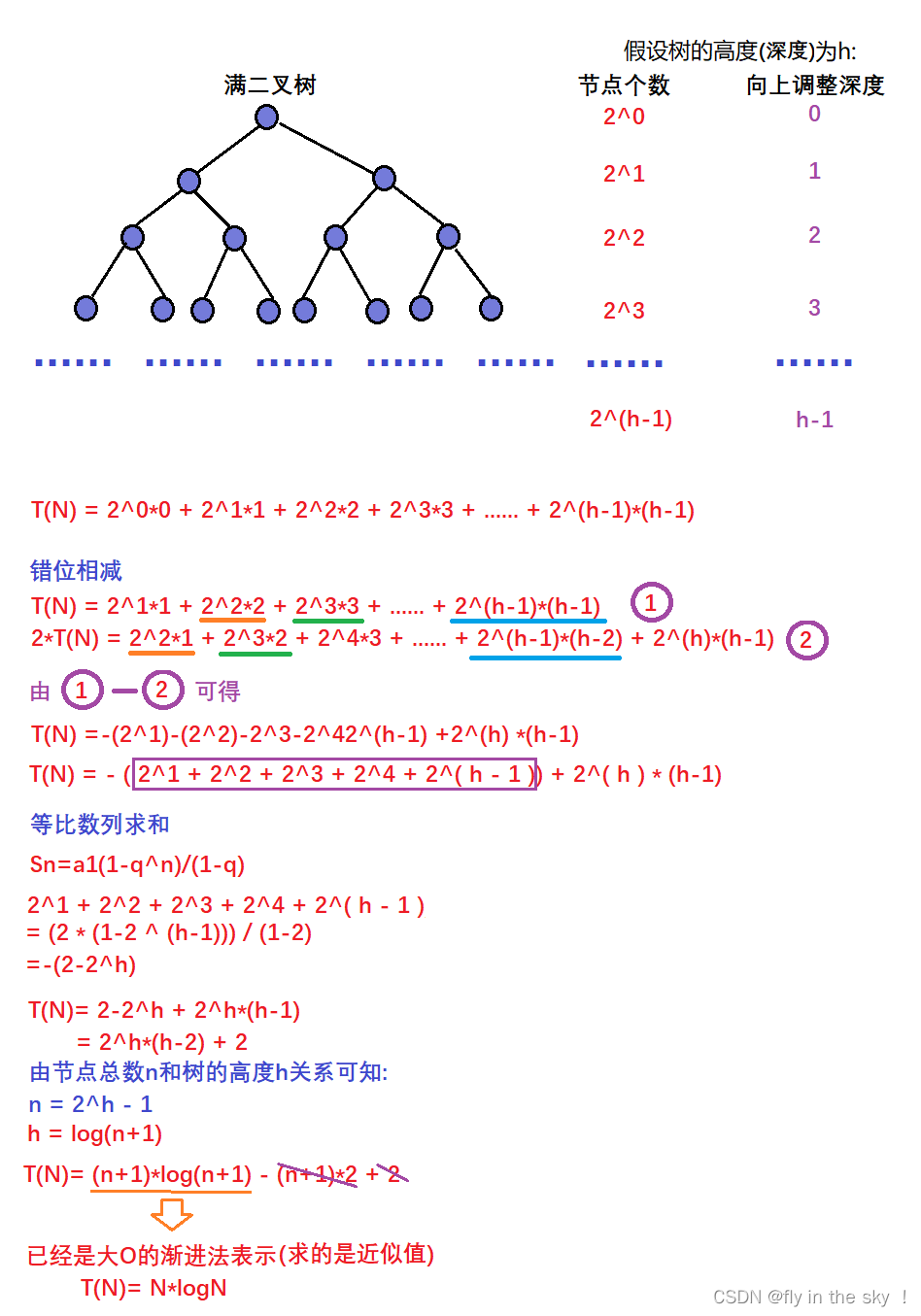
3.相关代码
//向上调整来建堆,时间复杂度为 O(n*logN)
Queue<Integer> minHeap = new PriorityQueue<>();
for (int i : arr) {
minHeap.offer(i);
}
//向上调整
private void shiftUp(int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (elem[child] > elem[parent]) {
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
child=parent;
parent = (child - 1) / 2;
} else {
break;
}
}
}
用向下调整建堆的时间复杂度
1.建堆的时间复杂度为O(N)
2.数学论证

3.相关代码
/*
* 创建大根堆的时间复杂度:O(N)
* 以满二叉树(挂的节点最多,是特殊的完全二叉树)来分析
* */
public void createHeap() {
for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {
shiftDown(parent, usedSize);
}
}
/*
* 父亲下标
* 每棵树的结束下标
* */
private void shiftDown(int parent, int len) {//向下调整
int child = parent * 2 + 1;
//最起码 要有左孩子
while (child < len) {
//一定是有右孩子的情况下
if (child + 1 < len && elem[child] < elem[child + 1]) {
child++;
}//点评:这代码写得有意思!!!
//child下标一定是左右孩子 最大值的下标
if (elem[child] > elem[parent]) {
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
parent = child;
child = 2 * parent + 1;
} else {
break;
}
}
}完结撒花✿✿ヽ(°▽°)ノ✿✿