📘前言：

C语言中，如果想存储一个整型，那么我们可以通过创建一个整型变量去存储一个数，如果想要存储一组相同类型的数，如果依次创建变量会显得很繁琐，C语言中提供了数组的概念，可以将一组相同类型的数据一次存储起来。数组—— 一组相同类型元素的集合。

🌟一维数组：

创建

数组的创建方式：

例如：
int arr[10];
这个声明定义了一个arr数组，其中有10个元素，每个元素都是整型。
📙注意：

针对 const_n 有两种情况：

C99 标准中引入了变长数组的概念，使得数组在创建的时候可以使用变量，但是这样的数组不能初始化。
例如: gcc环境下,int n = 0; int arr[n];
C99 标准之前，数组的大小只能是常量表达式。例如：VS2022,VS2019等IIDE下,int arr[10];

初始化

初始化：在创建数组的同时给数组的内容一些合理初始值。
初始化的一些方式：

完全初始化：
int arr[5] = { 1,2,3,4,5 };
不完全初始化：
int arr[5] = { 1,2,3 };剩余的元素都默认是 0.
int arr[5] = { 0 };第一个元素被赋值0，其他元素默认为0，使得全部元素被赋0.
省略数组大小：
int arr[] = {1,2,3,4,5}; 省略数组的大小后，数组必须初始化，数组的元素个数根据初始化的内容来确定。
char arr[] = "abc"; 4 个元素。
char arr[] = { 'a','b','c' }; 3个元素
char arr[] = { 97,'b','c' };数组内容与第二个一摸一样。

使用

数组下标是用来访问数组里每个元素的唯一标识符，每个数组的元素都有自己的下标，数组下标是从0开始，依次递增。

例如：

想要访问数组元素，就需要使用操作符 [ ] (下标引用操作符)，它其实就是数组访问的操作符。
[ ] 有两个操作数，一个是数组名称，一个是下标，例如：想要访问第一个元素，只需要 arr[0] 即可。所以，我们很容易就可以拿到数组的每个元素。
例如：

#include<stdio.h>
int main()
{
	int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	int i = 0;
	for (i = 0; i < sz; i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

存储表现

将int arr[] = { 1,2,3};每个元素的地址打印一下：

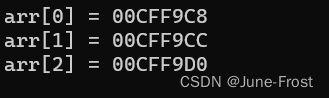
可以发现每个元素地址的差为4，而一个地址管理一个字节，这意味着地址之前有4个字节，也就是1个整型。
如图：

通过观察地址，我们可以发现：数组在内存中是连续存放的。并且，随着数组下标的增长，元素的地址，也在有规律的递增。

🌟二维数组：

二维数组是一种特殊的数组，它由一个或多个行和列组成，可以一次存储多组数据。

创建

基本形式：

例如：int arr[3][4] 创建了一个3行4列的数组，每个元素都是int。

初始化

初始化的一些方式：

完全初始化：
int arr[2][2] = { 1,2,3,4 };
int arr[2][2] = { {1,2},{3,4} };
不完全初始化：
int arr[3][4] = { 1,2,3,4 };
int arr[3][4] = { {1,2},{3,4} };
省略行：
int arr[][2] = { {1,2},{3,4} };
int arr[][4] = {1,2,3,4,5};
二维数组有初始化，行可以省略，列不可以省略。

使用

二维数组的使用同一维数组一样，通过下标访问元素。
int arr[3][4] = { {1,2,3,4},{3,4,5,6},{5,6,7,8} };

例如，访问整型8 ，arr[2][3] 即可。这样就可以遍历访问每一个元素。

#include<stdio.h>
int main()
{
	int arr[3][4] = { {1,2,3,4},{3,4,5,6},{5,6,7,8} };
	int row = 0;
	for (row = 0; row < 3; row++)
	{
		int col = 0;
		for (col = 0; col < 4; col++)
		{
			printf("%d ", arr[row][col]);
		}
		printf("\n");
	}
	return 0;
}

存储表现

将上述例子的地址打印出来：

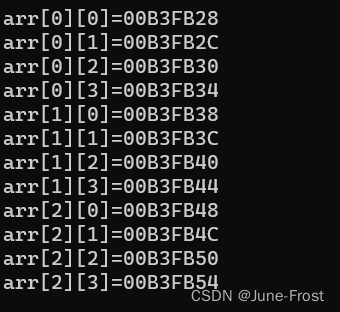
可以发现，二维数组在内存中也是连续存储的（从低地址到高地址）。所以我们可以将二维数组看作是一维数组的集合。

🌟数组越界

数组的下标是有范围限制的。
数组的下标规定是从0开始的，如果数组有n个元素，最后一个元素的下标就是n-1。所以数组的下标如果小于0，或者大于n-1，就是数组越界访问了，超出了数组合法空间的访问。
C语言本身是不做数组下标的越界检查，编译器也不一定报错，但是编译器不报错，并不意味着程序就是正确的

🌟数组名的含义

观察上图，可以发现数组名是首元素地址。

但是如果是&arr，则是取出了整个数组的地址，+1直接跳过了整个数组。不仅如此，在计算数组大小时sizeof(arr),这里的arr也是整个数组。
所以针对这些情况，有着如下结论：

sizeof(数组名)，计算整个数组的大小，sizeof内部单独放一个数组名，数组名表示整个数组
&数组名，取出的是数组的地址。&数组名，数组名表示整个数组
除上述两种情况外，通常数组名是数组首元素的地址。

🌟冒泡排序

要求：将一个整型数组的数据排列为升序。例如：将 9 8 7 6 5 4 3 2 1排列为 1 2 3 4 5 6 7 8 9 。

冒泡排序的核心思想为两两相邻的元素进行比较。每一趟冒泡排序使得一个数字到达最终应该出现的位置。

例如:第一趟冒泡排序，将9放到最大位置处。

如果按照上面的例子，排列10个数就需要9趟冒泡排序。(排列n个数最差情况需要排列n-1次）。
第一趟冒泡排序(将9归位)需要对比9次，第二趟冒泡排序(将8归位)需要对比8次，第七趟冒泡排序(将7归位)需要对比7次，依次类推。

代码如下:

#include<stdio.h>
void bubble_sort(int arr[10], int sz)
{
	int i = 0;
	for (i = 0; i < sz-1; i++)
	{
		int flag = 1; //标记
		int j = 0;
		for (j = 0; j < sz - 1 - i; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				flag = 0;
				int temp = 0;
				temp = arr[j + 1];
				arr[j + 1] = arr[j];
				arr[j] = temp;
			}
		}
		if (flag == 1)//如果等于1表示数组数据已经有序
		{
			break;
		}
	}
}
int main()
{
	int arr[10] = { 9,8,7,6,5,4,3,2,1,0 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	bubble_sort(arr,sz);
	int i = 0;
	for (i = 0; i < sz; i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}