这一章的内容主要讲并联机器人的相关算法，内容在全书中属于比较少，仅仅介绍概念的章节。

恰好部门中有一位同事就是专门做并联机器人出身的博士，也请他帮忙看了一下内容，但他觉得写书的这个人可能也不是非常懂并联机器人，他认为书里的一些内容表述的不是非常恰当。好在这节的内容偏向科普性质，而我司目前也并没有用到并联机器人，所以这节草草记录一下概念重点，等工作中如果遇到的时候再去深入，到时补充在这章。

---

概念 

包含一个或多个环路的运动链叫闭链。

通过一组“腿”连接动静平台所组成的闭链机构叫并联机构。

Stewart-Gough平台（六条P关节支撑动静平面的并联机器人）目前广泛用在运动模拟器和六轴力或力矩传感器。

闭链特征：1.并非所有关节都需要驱动 2.关节变量必须满足若干约束方程。

驱动关节的数目如果超过机构自由度，即称为“冗余驱动”。

闭链机器人的正逆运动学

特点：与串联机器人相反，并联机器人的逆运动学相对简单，正运动学相对复杂，因为任意一组关节值可能不可行，或平台多组位移。

明确：正运动学的输入一定是驱动副。正是因为驱动副的作用下，非驱动副可能跑到不同的位置，这样导致末端（动平台）的位置不固定，所以并联机器人的正运动学可能有多解。

比如地面有两个驱动的R关节向上连着连杆，然后两个连杆上方各有一个被动的R关节，这俩被动的R关节又各引伸出一个连杆交会到中间的一个公共的被动R关节上。

可以想象一下这个下面俩主动关节，上面三个被动关节的口字形并联机器人，如果下面俩关节都往中间缩45度，那么上面的三个关节，两个连杆，可能向下伸，也可能向上伸。所以会导致多解。

那如果FK的输入连同被动副也送进去了，那就不可能是多解了，除非见鬼。当然很大概率是直接导致过约束，现在的机构满足不了你的要求，直接无解。

3-RPR平面并联机构 

 

 

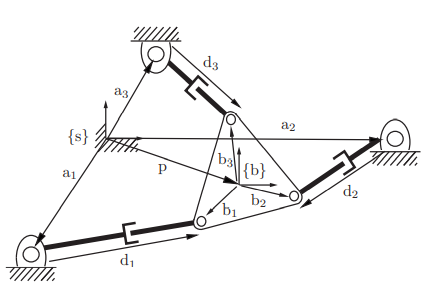
中间那个三角形即为动平台，逆解就是把向量串起来，涉及到的向量有pbad。

即：d=p+b-a

可以看到只有b向量是在{b}系下的，其他向量都在{s}系下，(这里中文版151页印刷错误）

因此这个等式相加，需要把所有的变量都转到同一个坐标系下。即b前面需要左乘Rsb，都转到S系下才方便相加。

 我们观察此公式，发现d其实是逆解的结果，因为d是平动副P关节的变量，而Rsb，p是末端的位姿，ba是常量，所以逆运动学非常简单，直接算就好了。

那如果反过来，根据dba算p和Rsb，那就不那么简单。需要把上面的公式开平方算模长，（即dx和dy的平方是p关节的移动长度），再把sin和cos，用高等数学学过的替换公式代替：

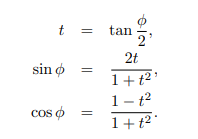
这样组成一套公式，把三条腿的s全代入，构造方程才能最终解出t和p，得到正解结果。

正解结果也可能不唯一，比如奇异位形：

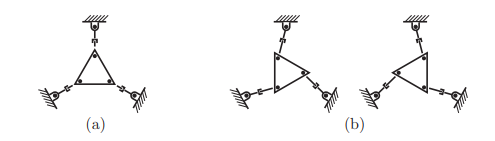
 把腿伸长可能会让三角形顺时针或者逆时针转，或者直接把平台怼坏掉。。

Stewart-Gough平台

 这个其实和平面3RPR并联机器人的解法是一样的，都是构建公式，

 逆解和上面平面部分一样，正解则是假设一个矩阵R，和p，然后6条腿会得到六个约束方程（套入到上面的s平方公式里），然后再有个RRT=I的约束（会提供6个，参见第40页）也有六个约束，所以得到了12个方程组求解完才能得到正解结果。

一般并联机构

一个静平台，上面盯着三条腿，每条腿分别有n，m，p个R关节。

后面叙述的有些迷惑，我这里直接替作者重新描述：

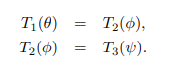
这里两个公式。

每个公式中：两矩阵相等，即12个变量相同，其实就是齐次矩阵去掉最后一行，剩12个元素，然后12个元素相等，就是12个方程。两个公式则是12*2=24个方程。

然后看约束有多少个，R是9个元素，但本质上只有3个自由变量，所以两个公式里各有3个旋转+3个平移=6个自由变量，一共12个自由变量，那么24个方程就提供了24-12=12个约束。

所以机构自由度就是n+m+p-12个自由度。（这里的12是来源于上一段算出来的12个约束）

好了，到这里就好了，上面说的感觉有问题，你觉得理解不清楚我也没办法，本来这里讲的就有点让人迷糊。

然后确定真正的腿长向量，反解各个关节就行了。文中“这不简单，可能有多解”，指的不是前文说的并联机器人的正解可能有多解，它实际指的是下面一条腿当作串联机器人看，逆解求关节角可能有多解。这里写的很迷糊，但不是翻译人员的锅，原书写的就很迷糊。

那么得到关节角后，在这个机构上算顶端的正解，实际上还是比较容易的。

微分运动学

概念：

1.只有驱动关节确定输入速度，被动关节由约束方程决定。

2.并联机器人除了前向运动学的雅可比矩阵，多了一个约束雅可比矩阵（其实就是逆运动学雅可比），即通过运动约束方程确定的雅可比矩阵。（求逆即可转为正运动学雅可比，当然不可逆则可以用伪逆来，参见IK这节：【现代机器人学】学习笔记五：逆运动学（Inverse kinematics）_zkk9527的博客-CSDN博客）

Stewart-Gough平台

速度学

学到这里以后其实我们都知道，在串联机器人里，得知关节速度，左乘前向运动学的雅可比矩阵，就能得到末端速度。

那么在这里，正解容易，反解困难，所以难的是通过平台速度算腿的速度。

所以这里就是，根据平台速度，左乘逆向运动学的雅可比矩阵，就能得到关节速度。

静力学

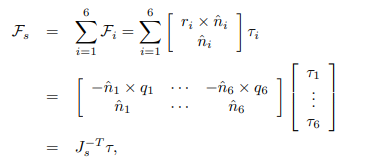
这里就是把力旋量（上面力矩，下面力）拆成6腿叠加的形式，然后n是力的方向，r是力臂，tao是力的大小（不同于串联机器人部分，这里tao是力而不是力矩）。

r作为力臂，是s系原点到球铰，基坐标系的球铰向量用q表示，不知道为什么推导的时候用了把位置调换然后加了负号，我猜可能是想写成串联机器人那块雅可比-wxq的形式一致。

回顾静力学部分：【现代机器人学】学习笔记四：一阶运动学与静力学_zkk9527的博客-CSDN博客

力旋量左乘雅可比的转置等于关节力矩

注意：

从关节空间转换至笛卡尔空间：

关节速度左乘雅可比为末端旋量，而关节力矩左乘雅可比的（逆转置）为末端力旋量

这个非常容易记错了，提到力，我们就说“逆转置”来记忆。

 

 所以反过来，其实就是：

所以这个公式成立的，其中tau 可能是关节力矩，也可能是力。但这里是P关节提供支撑的力的，它不是旋转关节提供的，所以力旋量分别可以和力或者力矩通过雅可比矩阵建立联系。

那么在这里，J仍然是FK的雅可比矩阵。（可以看看对于这种平台的FK的雅可比原来可以这样算）

ps：这章安排有点奇怪，大题目是微分运动学，但这里又插入静力学的内容有点莫名其妙。

一般并联机构

先提前说这节想干什么，以避免读者看晕：这一小节想用驱动副的速度推被动副的速度，这是串联机器人里用不到的。

这里还是，先让两个公式相等：

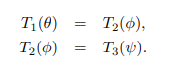
然后根据旋量和T的公式得到旋量相等，（其实完全可以直接旋量相等）

旋量等于雅可比左乘关节速度，所以得到

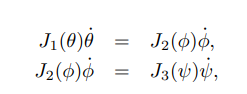
然后移项，用矩阵表示，得到：

 

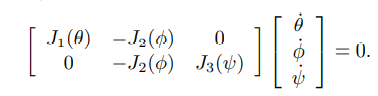
 然后改写矩阵，摘出驱动副和被动副（假设只有第一个关节是驱动副），得到：

 

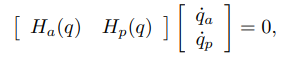
 这里a是actuator，即驱动副，p是passive，则是被动副。

所以被动副速度就是：

 只要被动副对应的Hp可逆，这里就能从驱动副的速度推算被动副的速度。

后面的内容写的挺拉跨的，感觉这个作者似乎确实也不太擅长讲并联机器人的理论，我认为不重要，就不放这里了。

并联机器人奇异

位形空间奇异

这个学术点讲，就是位形空间出现分叉点。这种会导致逆运动学的约束雅可比降秩。

驱动奇异

这个则看上面分开主动副和被动副部分的H矩阵（注意这个矩阵和雅可比矩阵有关，但是并不是雅可比矩阵），被动副部分的H矩阵不满秩，则是驱动奇异。

说白了，就是被动副可能出现不可预测运动的时候，就是驱动奇异。

那么驱动奇异又分为非退化奇异和退化奇异：

什么叫非退化呢，就是我最开始说的那个口字形的不可预测问题，关节不能随便活动（所以这里叫非退化），但是不可预测。即：驱动关节不能被独立驱动。

退化奇异则是关节能随便活动。即：锁定所有关节不能使系统保持刚性。

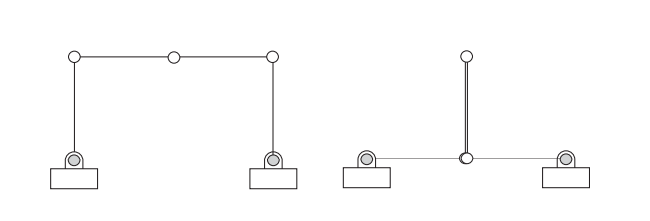
 换驱动副就能解决这种奇异问题。

末端奇异

末端奇异就类似于我们常见的开链串联机器人的奇异了，就是末端不能执行某一方向的速度。

判断方法则是：先排除并联机器人的驱动奇异问题，然后像开链机器人那样，用雅可比矩阵是否满秩来确认是不是末端奇异。

末端奇异和驱动副选择无关。

---

确实，学完这节感觉，并联机器人变化无穷，比串联机器人要复杂很多。

这也可能是导致这节不能很详细的讲的原因，因为单独并联机器人就可以展开好几本书了。

不过暂时用不到那许多内容，因此目前先展开这些概念，后续有需要我再补充。