LC-将有序数组转换为二叉搜索树

链接：https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/description/

描述：
给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡二叉搜索树。
高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

例1：
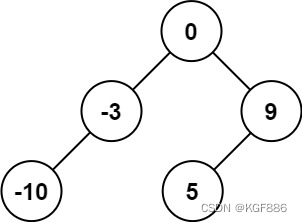
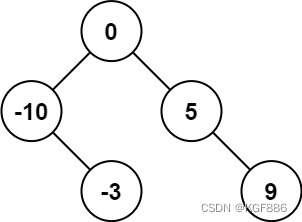
在这里插入图片描述

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

例2：
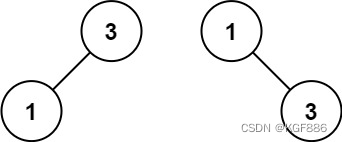
在这里插入图片描述

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

前言：
二叉搜索树的中序遍历是升序序列，题目给定的数组是按照升序排序的有序数组，因此可以确保数组是二叉搜索树的中序遍历序列。
给定二叉搜索树的中序遍历，是否可以唯一地确定二叉搜索树？答案是否定的。如果没有要求二叉搜索树的高度平衡，则任何一个数字都可以作为二叉搜索树的根节点，因此可能的二叉搜索树有多个。
如果增加一个限制条件，即要求二叉搜索树的高度平衡，是否可以唯一地确定二叉搜索树？答案仍然是否定的。
直观地看，我们可以选择中间数字作为二叉搜索树的根节点，这样分给左右子树的数字个数相同或只相差 111，可以使得树保持平衡。如果数组长度是奇数，则根节点的选择是唯一的，如果数组长度是偶数，则可以选择中间位置左边的数字作为根节点或者选择中间位置右边的数字作为根节点，选择不同的数字作为根节点则创建的平衡二叉搜索树也是不同的。
确定平衡二叉搜索树的根节点之后，其余的数字分别位于平衡二叉搜索树的左子树和右子树中，左子树和右子树分别也是平衡二叉搜索树，因此可以通过递归的方式创建平衡二叉搜索树。
当然，这只是我们直观的想法，为什么这么建树一定能保证是「平衡」的呢？这里可以参考「1382. 将二叉搜索树变平衡」，这两道题的构造方法完全相同，这种方法是正确的，1382 题解中给出了这个方法的正确性证明：1382 官方题解，感兴趣的同学可以戳进去参考。

思路：整个树为平衡二叉树，则每个节点自身肯定要是平衡的，所以可以递归处理。每次取中间点为根节点，左边的作为根节点的左子树，右边的做为右子树。
代码如下：

    public TreeNode sortedArrayToBST(int[] nums) {
        //数组为空时返回null
        if(nums.length == 0){
            return null;
        }
        //当数组只有一个值时新建节点即可
        if(nums.length == 1){
            return new TreeNode(nums[0]);
        }
        //获取中间点下标
        int index = nums.length>>>1;
        //根据中间点的值创建根节点
        TreeNode root = new TreeNode(nums[index]);
        //截取数组，左边的是当前节点左子树的值，右边是右子树的值
        int[] temp = new int[index];
        int[] temp2 = new int[nums.length-1-index];
        System.arraycopy(nums,0,temp,0,index);
        System.arraycopy(nums,index+1,temp2,0,nums.length-1-index);
        //递归处理
        root.left = sortedArrayToBST(temp);
        root.right = sortedArrayToBST(temp2);
        return root;
    }