目录
1.直接插入排序
2.希尔排序
3.简单选择排序
4.堆排序
5.冒泡排序
6.快速排序
7.归并排序
8.基数排序(桶排序)
9.主函数
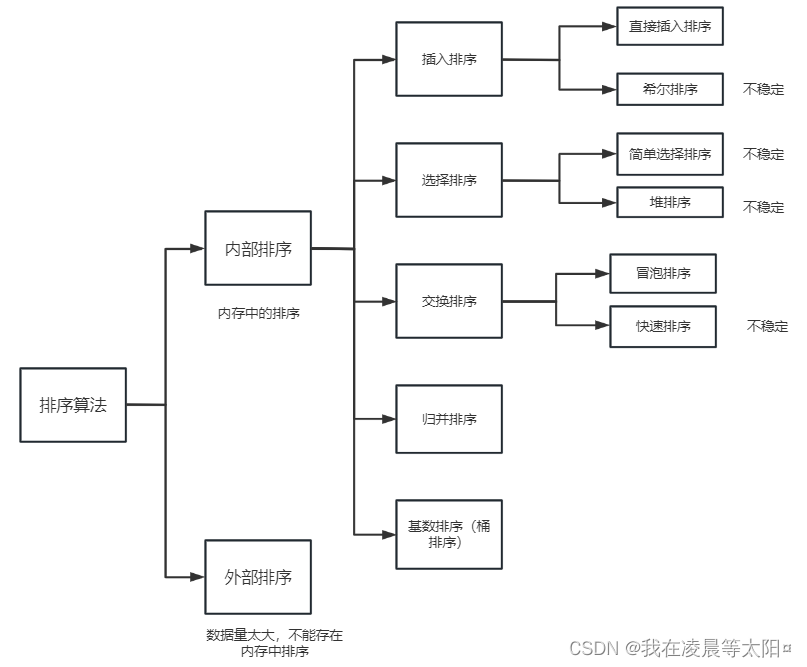
10.画图总结
1.直接插入排序
int ai[] 为需要排序的数组
start 为起始位置,要求 start>=1 ,因为 ai[0] 要作为“哨兵”使用。
end 为结束位置
代码思路:看后面的数字有没有比前面的大,比前面的大则需要插入交换,从后往前,依次比较,依次往后移一位,直到不满足
void InsertSort(vector<int>&arr, int len)
{
int tmp = 0;
for (int i = 1; i < len; i++)//第一张扑克牌无需比较
{
tmp = arr[i];
if (arr[i] < arr[i - 1])//满足需要交换的条件
{
for (int j = i - 1; j >= 0&&arr[j]>tmp; j--)//这里多加了一个判断,因为之前if语句进入之后,第一次循环没有问题,但当第二次及之后的循环开始,没有这个判断,代码会直接交换,不在乎大小
{
arr[j+1] = arr[j];
arr[j] = tmp;
}
}
}
}2.希尔排序
希尔排序:进阶版的直接插入排序
-
原理:将一组数进行分组,比如按5 3 1分组,就是开始五个数为一组,再3个数,最后一个数,分组后,每一组的第一个相互比较,观察满不满足交换条件,依次第二个、第三个,直到这个分组的数比较完成,再开始下一个分组
-
算法的优点在于它首先保证局部的大致有序,让最后的直接插入排序交换的次数减少
void ShellSort(vector<int>& arr, int len)
{
int inc = 0, i = 0, j = 0, tmp = 0;
//inc是初始增量,每次除2
for (inc = len / 2; inc >0; inc /= 2)
{
//插入排序
for (i = inc; i < len; i++)
{
tmp = arr[i];
for (j = i; j >= inc&&tmp<arr[j-inc]; j-=inc)
{
arr[j] = arr[j-inc];
}
arr[j] = tmp;
}
}
}3.简单选择排序
简单选择排序:一直寻找剩余数组中最小的元素放到前面
void SelectSort(vector<int>& arr, int len)
{
int tmp = 0;
for (int i = 0; i < len - 1; i++)
{
for (int j = i + 1; j < len; j++)
{
if (arr[i] > arr[j])//因为这里一直是和i所在位置的元素比,所以不是像冒泡排序一样全部用j
{
tmp = arr[j];
arr[j] = arr[i];
arr[i] = tmp;
}
}
}
}4.堆排序
-
堆排序:堆调整+堆排序
-
将最开始的数组构建完全二叉树,通过堆调整让最大的数出现在根节点上,交换根节点与最后一个节点,将除最后一个节点的其他数再次调整,最大的数位于根节点,以此类推
void Adjust(vector<int>& arr, int len, int index)
{
int left = 2 * index + 1;//左孩子
int right = 2 * index + 2;//右孩子
int maxIdx = index;
if (left<len && arr[left]>arr[maxIdx])maxIdx = left;
if (right<len && arr[right]>arr[maxIdx])maxIdx = right;//经过两个if判断后,maxIdx是父节点以及两个叶子节点之中最大值的下标
if (maxIdx != index)//maxIdx如果发生变化
{
swap(arr[maxIdx], arr[index]);//交换下标对应的值,让最大值处于根节点
Adjust(arr, len, maxIdx);//继续调整
}
}
void HeapSort(vector<int>&arr,int len)
{
for (int i = len / 2 - 1; i >= 0; i--)
{
Adjust(arr, len, i);//从最下层的非叶子节点开始调整
}
for (int i = len - 1; i >= 1; i--)//这里i不取0是因为剩余一个数的时候不用交换
{
swap(arr[0], arr[i]);//根节点的数与结尾的数进行交换,再次循环去调整
Adjust(arr, i, 0);//寻找最大的数放到根节点,重复以上步骤
}
}5.冒泡排序
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
void BubbleSort(vector<int>& ai, int len)
{
int i = 0, j = 0,tmp=0;
for (i=0; i < len-1; ++i)//比如10个数只用9趟排序就可以
{
for (j=0;j < len -1-i; j++)
{
if (ai[j] > ai[j + 1])
{
tmp = ai[j];
ai[j] = ai[j + 1];
ai[j + 1] = tmp;
}
}
}
}6.快速排序
划分函数+递归调用
-
以第一个数为基准,将所有数按照基准划分左右,左边小,右边大,对左子序列和右子序列重复以上操作
int Part(vector<int>& arr, int low, int high)
{
int pivot = arr[low];//一般以第一个数为基准
int i = low, j = high;
while (i < j)
{
while (i < j && arr[j] > pivot)
{
j--;
}
if (i < j)//走到这说明上个while循环的第二个条件是不满足的
{
swap(arr[i], arr[j]);
i++;
}
while (i < j && arr[i] <= pivot)
{
i++;
}
if (i < j)
{
swap(arr[i], arr[j]);
j--;
}
}
return i;//返回最后基准划分所在的下标
}
void QuickSort(vector<int>& arr, int left, int right)
{
int mid = 0;
if (left < right)
{
mid = Part(arr, left, right);
QuickSort(arr, left, mid - 1);//等到这里失败才会进行下面的递归,所以 这里失败的时候就是已经有序的情况
QuickSort(arr, mid + 1, right);
}
}7.归并排序
归并排序:将数组进行分组,保证组内有序,分成最小的组也就是一个数组一组,因为默认一个数字就是有序,所以开始两两一组排序,有序的合并两两一组就变成了四个数一组,依次递增,直到最后合并为一组
void Merge(vector<int>& arr,int *temp, int left, int mid, int right)
{
int k = left, i = left, j = mid + 1;
while (i != mid+1 && j <= right)
{
if (arr[i] <= arr[j])temp[k++] = arr[i++];
else
{
temp[k++] = arr[j++];
}
}
while (i <= mid)
{
temp[k++] = arr[i++];//右边数据已经放完,将左边已经有序的数据放入temp中
}
while (j <= right)
{
temp[k++] = arr[j++];//左边数据已经放完
}
for (int i= 0;i< k ; i++)
{
arr[i] = temp[i];
}
}
void MergeSort(vector<int>& arr,int *temp, int left, int right)
{
if (left == right)
{
return;
}
else
{
int mid = left + (right-left) / 2;
MergeSort(arr, temp,left, mid);
MergeSort(arr,temp, mid + 1, right);
Merge(arr,temp,left, mid, right);
}
}8.基数排序(桶排序)
以最大的数的位数为标准,比如最大数是255,最高位是百位,那么就进行三次排列,将每个数的个位放入对应的桶,桶从0-9,比如277,第一步个位为7,所以放入下标为7的桶中,依次放入所有的数,由于可能有多个数的个位相同,所以这个桶是一个二维数组;最后把二维数组里的数又放回原始数组里,完成第一趟排序,但这样存在一个问题就是有些桶可能没有数据,不需要遍历,所以增加一个数组bucketIndex来记录每个桶内放入多少数据;遍历的时候加上这个限制,最后,把下标桶(bucketIndex)中的数据清零,至此,完成了第一次排序。
void RadixSort(vector<int>& arr, int len)
{
//1.找出最大值
int max = arr[0];
int bucket[10][1000];//这里必须给常量值,这个二维数组是存放数据的数组
int bucketIndex[] = { 0,0,0,0,0,0,0,0,0,0 };//记录0-9这些桶里是否有数据
for (int i = 1; i < len; i++)
{
max = arr[i] > max ? arr[i] : max;
}
int divisor = 1;//控制最大数获取各个位的数,比如获取个位除1然后%10就可,获取十位就是除以10然后%10
//2.循环找出最大值的位数
while (max > 0)
{
//遍历数组放入桶中
for (int i = 0; i < len; i++)
{
int temp = arr[i]/divisor%10;//依次求出这个数的个位十位等
bucket[temp][bucketIndex[temp]] = arr[i];
bucketIndex[temp]++;//计数加加
}
//3.把桶中的数据重新赋值给原始数组
int index = 0;
for (int i = 0; i < 10; i++)
{
if (bucketIndex[i] != 0)//代表有数据
{
for (int j = 0; j < bucketIndex[i]; j++)
{
arr[index++] = bucket[i][j];
}
}
}
//4.清空下标桶
for (int i = 0; i < 10; i++)
{
bucketIndex[i] = 0;
}
divisor *= 10;
max /= 10;
}
}
9.主函数
void main()
{
int ar[] = { 8, 1,200, 14, 3, 21, 5, 7, 10 ,0};
int len = sizeof(ar) / sizeof(ar[0]);
vector<int>arr(ar, ar +len);
int* brr = new int[len];
BubbleSort(arr, len);//冒泡排序
cout << "冒泡排序: ";
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
InsertSort(arr, len);//直接插入
cout << "直接插入排序: ";
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
ShellSort(arr, len);//希尔排序
cout << "希尔排序: ";
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
SelectSort(arr, len);//简单选择排序
cout << "简单选择排序: ";
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
HeapSort(arr, len);//堆排序
cout << "堆排序: ";
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
QuickSort(arr, 0, len - 1);//快速排序
cout << "快速排序: ";
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
MergeSort(arr,brr, 0, len-1);//归并排序
cout << "归并排序: ";
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
RadixSort(arr, len);//基数(桶)排序
cout << "基数(桶)排序:";
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
delete[]brr;
brr = nullptr;
}截图: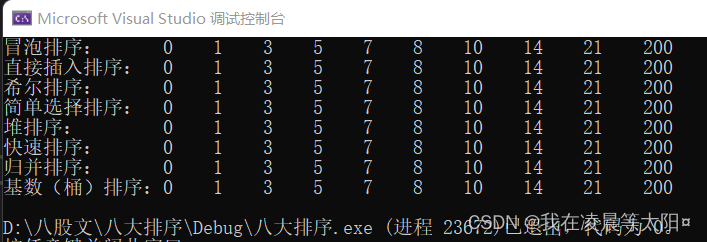
10.画图总结