决策树(DecisionTree)学习是以实例为基础的归纳学习算法。算法从--组无序、无规则的事例中推理出决策树表示形式的分类规则,决策树也能表示为多个If-Then规则。一般在决策树中采用“自顶向下、分而治之”的递归方式,将搜索空间分为若千个互不相交的子集,在决策树的内部节点(非叶子节点)进行属性值的比较,并根据不同的属性值判断从该节点向下的分支,在树的叶节点得到结论。
数据挖掘中的分类常用决策树实现。到目前为止,决策树有很多实现算法,例如1986年由Quinlan提出的ID3算法和1993年提出的C4.5算法,以及CART,C5.0(C4.5的商业版本),SLIQ和SPRINT等。本章将详细讲解ID 3算法和C 4.5算法的基本思想,并结合实例讲解在MATLAB环境
下利用决策树解决分类问题。

1.案例背景

1. 1 决策树分类器概述

        1)决策树分类器的基本思想及其表示
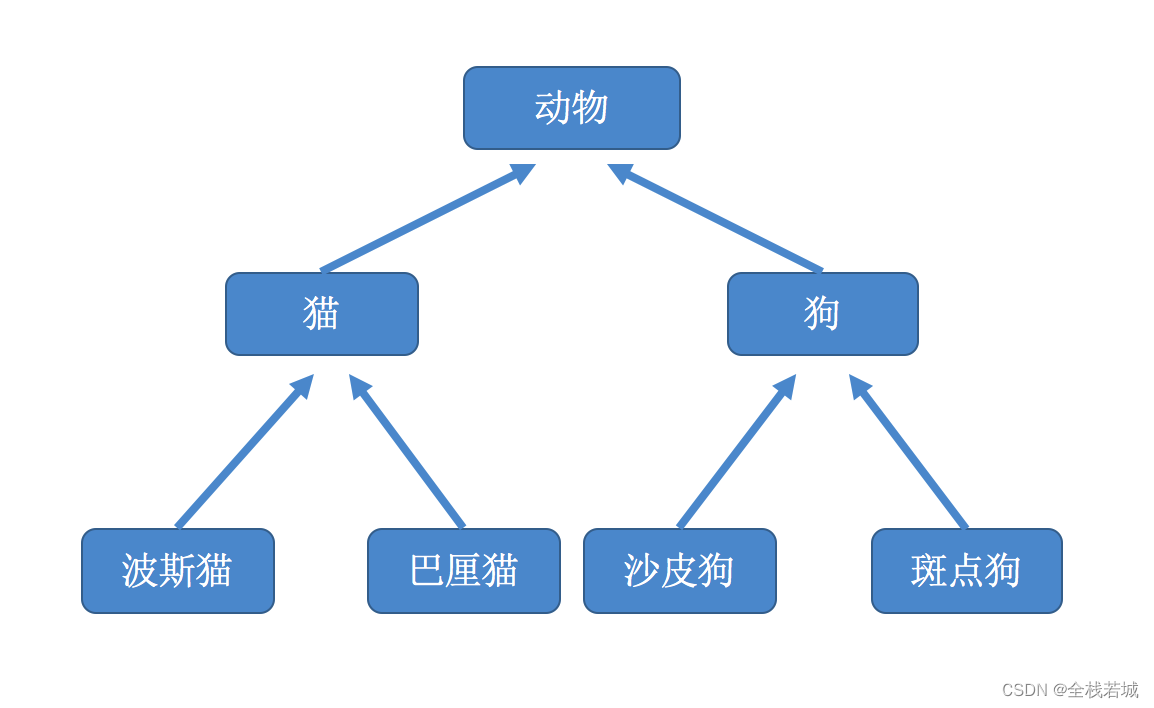
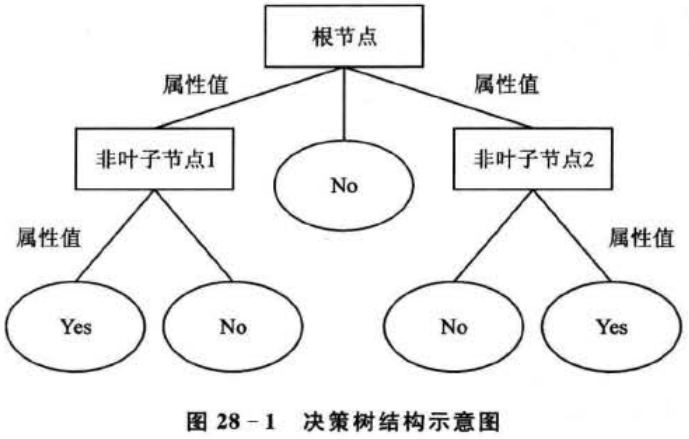
        决策树通过把样本实例从根节点排列到某个叶子节点来对其进行分类。树上的每个非叶子节点代表对一个属性取值的测试，其分支就代表测试的每个结果;而树上的每个叶子节点均代表一个分类的类别，树的最高层节点是根节点。
        简单地说,决策树就是一个类似流程图的树形结构,采用自顶向下的递归方式,从树的根节点开始,在它的内部节点上进行属性值的测试比较,然后按照给定实例的属性值确定对应的分支,最后在决策树的叶子节点得到结论。这个过程在以新的节点为根的子树上重复。图28-1所示为决策树的结构示意图。在图上，每个非叶子节点代表训练集数据的输人属性,Attribute Value代表属性对应的值,叶子节点代表目标类别属性的值。图中的“Yes”、“No”分别代表实例集中的正例和反例。

2)ID3算法
到目前为止,已经有很多种决策树生成算法,但在国际上最有影响力的示例学习算法首推J. R. Quinlan的ID 3(Iterative Dichotomic version 3)算法。Quinlan的首创性工作主要是在决策树的学习算法中引入信息论中互信息的概念,他将其称作信息增益(information gain),以之作为属性选择的标准。

为了精确地定义信息增益,这里先定义信息论中广泛使用的一一个度量标准，称为熵(entropy),它刻画了任意样例集的纯度(purity)。如果目标属性具有c个不同的值,那么集合S相对于c个状态的分类的熵定义为

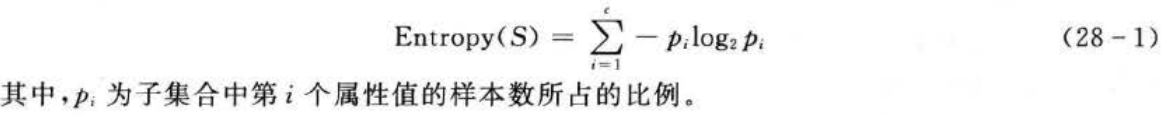
由上式可以得到:若集合S中的所有样本均属于同一类,则Entropy(S)=0;若两个类别的样本数不相等,则Entropy(S)∈(0,1)。
特殊地,若集合S为布尔型集合,即集合S中的所有样本属于两个不同的类别,则若两个类别的样本数相等,有Entropy(S)=1。图28-2描述了布尔型集合的熵与p;的关系。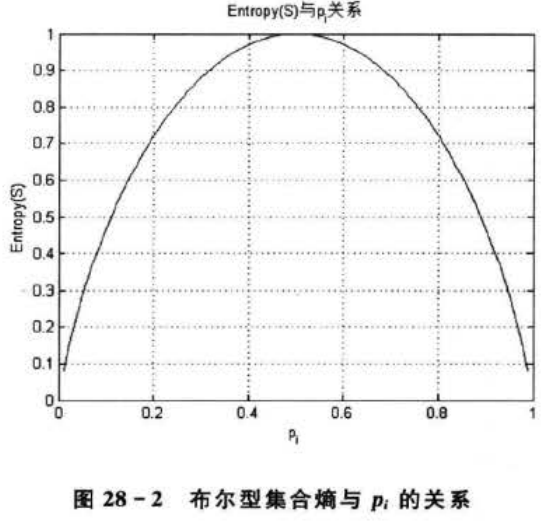

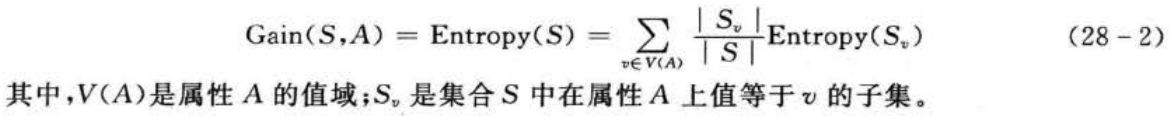
已经有了摘作为衡量训练样例集合纯度的标准，信息增益 Gain(S,A ）的定义为

        引入信息增益的概念后，下面将详细介绍ID3算法的基本流程。不妨设Examples为训练样本集合,Attributelist为候选属性集合。
        ①创建决策树的根节点N;
        ②若所有样本均属于同一类别C,则返回N作为-一个叶子节点,并标志为C类别;
        ③若Attributelist为空,则返回N作为一一个叶子节点,并标志为该节点所含样本中类别最多的类别;
        ④计算Attributelist中各个候选属性的信息增益，选择最大的信息增益对应的属性Attribute* ,标记为根节点N;
        ⑤根据属性Attribute*值域中的每个值V;,从根节点N产生相应的一个分支,并记S,为Examples集合中满足Attribute" =V,条件的样本子集合;
        ⑥若S,为空,则将相应的叶子节点标志为Examples样本集合中类别最多的类别;否则，将属性Attribute*从Attribute list 中删除,返回①,递归创建子树。
        3)C4.5算法
        针对ID3算法存在的一些缺点,许多学者包括Quinlan都做了大量的研究。C4.5算法便是ID 3算法的改进算法,其相比于ID3改进的地方主要有:
①用信息增益率(gainratio)来选择属性
        信息增益率是用信息增益和分裂信息量(splitinformation)共同定义的,关系如下:

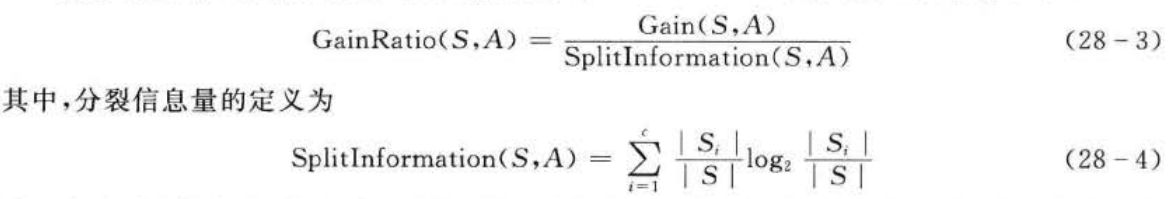
        采用信息增益率作为选择分支属性的标准,克服了ID3算法中信息增益选择属性时偏向选择取值多的属性的不足。
②树的剪枝
        剪枝方法是用来处理过拟合问题而提出的,一般分为先剪枝和后剪枝两种方法。先剪枝方法通过提前停止树的构造,比如决定在某个节点不再分裂,而对树进行剪枝。一旦停止,该节点就变为叶子节点,该叶子节点可以取它所包含的子集中类别最多的类作为节点的类别。
        后剪枝的基本思路是对完全成长的树进行剪枝,通过删除节点的分支,并用叶子节点进行替换,叶子节点一般用子集中最频繁的类别进行标记。
        C4.5算法采用的悲观剪枝法(PessimisticPruning)是Quinlan在1987年提出的,属于后剪枝方法的一种。它使用训练集生成决策树,并用训练集进行剪枝,不需要独立的剪枝集。悲观剪枝法的基本思路是:若使用叶子节点代替原来的子树后,误差率能够下降，则就用该叶子节点代替原来的子树。关于树的剪枝详尽算法,请参考本章的参考文献,此处不再赘述。
        4)决策树分类器的优缺点
        相对于其他数据挖掘算法,决策树在以下几个方面拥有优势:
        ①决策树易于理解和实现。人们在通过解释后都有能力去理解决策树所表达的意义。
        ②对于决策树,数据的准备往往是简单或者是不必要的。其他的技术往往要求先把数据归一化，比如去掉多余的或者空白的属性。
        ③能够同时处理数据型和常规型属性。其他的技术往往要求数据属性单--。
        ④是一个白盒模型。如果给定一个观察的模型,那么根据所产生的决策树很容易推出相应的逻辑表达式。

        同时,决策树的缺点也是明显的，主要表现为:
        ①对于各类别样本数量不一致的数据,在决策树当中信息增益的结果偏向于那些具有更多数值的特征。
        ②决策树内部节点的判别具有明确性,这种明确性可能会带来误导。

1.2 问题描述

威斯康辛大学医学院经过多年的收集和整理,建立了一个乳腺肿瘤病灶组织的细胞核显微图像数据库。数据库中包含了细胞核图像的10个量化特征(细胞核半径、质地、周长、面积、光滑性、紧密度、凹陷度、凹陷点数、对称度、断裂度),这些特征与肿瘤的性质有密切的关系。因此,需要建立一个确定的模型来描述数据库中各个量化特征与肿瘤性质的关系,从而可以根据细胞核显微图像的量化特征诊断乳腺肿瘤是良性还是恶性的。

2.模型建立

2.1 设计思路

将乳腺肿瘤病灶组织的细胞核显微图像的10个量化特征作为模型的输人，良性乳腺肿瘤和恶性乳腺肿瘤作为模型的输出。用训练集数据进行决策树分类器的创建,然后对测试集数据进行仿真测试,最后对测试结果进行分析。

2.2 设计步骤

根据上述设计思路,设计步骤主要包括以下几个部分，如图28-3所示。

        1)数据采集
        数据来源于威斯康辛大学医学院的乳腺癌数据集,共包括569个病例,其中,良性357例,恶性212例。本书随机选取500组数据作为训练集,剩余69组作为测试集。每个病例的一组数据包括采样组织中各细胞核的这10个特征量的平均值、标准差和最坏值(各特征的3个最大数据的平均值)共30个数据。数据文件中每组数据共分32个字段:第1个字段为病例编号;第2个字段为确诊结果,B为良性,M为恶性;第3~12个字段是该病例肿瘤病灶组织的各细胞核显微图像的10个量化特征的平均值;第13~22个字段是相应的标准差;第23~32个字段是相应的最坏值。
        2)决策树分类器创建
        数据采集完成后,利用MATLAB自带的统计工具箱函数ClassificationTree. fit(MATLAB R2012b)或classregtree(MATLAB R2009a) ,即可基于训练集数据创建一个决策树分类器。

        3)仿真测试
        决策树分类器创建好后,利用MATLAB自带的统计工具箱函数predict(MATLABR2012b)或eval(MATLAB R2009a),即可对测试集数据进行仿真预测。
        4)结果分析
        通过对决策树分类器的仿真结果进行分析,可以得到误诊率(包括良性被误诊为恶性、恶性被误诊为良性),从而可以对该方法的可行性进行评价。同时,可以与其他方法进行比较,探讨该方法的有效性。

3 决策树分类器编程实现

决策树分类器完整代码实现如下：

%% 决策树分类器在乳腺癌诊断中的应用研究

%% 清空环境变量
clear all
clc
warning off

%% 导入数据
load data.mat
% 随机产生训练集/测试集
a = randperm(569);
Train = data(a(1:500),:);
Test = data(a(501:end),:);
% 训练数据
P_train = Train(:,3:end);
T_train = Train(:,2);
% 测试数据
P_test = Test(:,3:end);
T_test = Test(:,2);

%% 创建决策树分类器
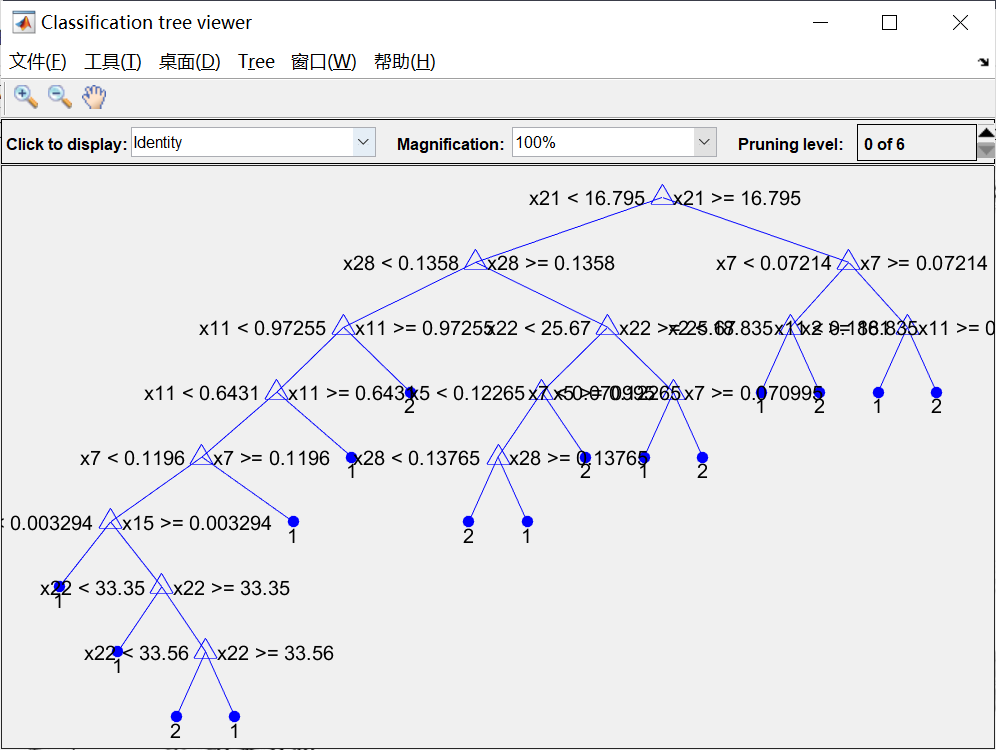
ctree = ClassificationTree.fit(P_train,T_train);
% 查看决策树视图
view(ctree);
view(ctree,'mode','graph');

%% 仿真测试
T_sim = predict(ctree,P_test);

%% 结果分析
count_B = length(find(T_train == 1));
count_M = length(find(T_train == 2));
rate_B = count_B / 500;
rate_M = count_M / 500;
total_B = length(find(data(:,2) == 1));
total_M = length(find(data(:,2) == 2));
number_B = length(find(T_test == 1));
number_M = length(find(T_test == 2));
number_B_sim = length(find(T_sim == 1 & T_test == 1));
number_M_sim = length(find(T_sim == 2 & T_test == 2));
disp(['病例总数：' num2str(569)...
      '  良性：' num2str(total_B)...
      '  恶性：' num2str(total_M)]);
disp(['训练集病例总数：' num2str(500)...
      '  良性：' num2str(count_B)...
      '  恶性：' num2str(count_M)]);
disp(['测试集病例总数：' num2str(69)...
      '  良性：' num2str(number_B)...
      '  恶性：' num2str(number_M)]);
disp(['良性乳腺肿瘤确诊：' num2str(number_B_sim)...
      '  误诊：' num2str(number_B - number_B_sim)...
      '  确诊率p1=' num2str(number_B_sim/number_B*100) '%']);
disp(['恶性乳腺肿瘤确诊：' num2str(number_M_sim)...
      '  误诊：' num2str(number_M - number_M_sim)...
      '  确诊率p2=' num2str(number_M_sim/number_M*100) '%']);
  
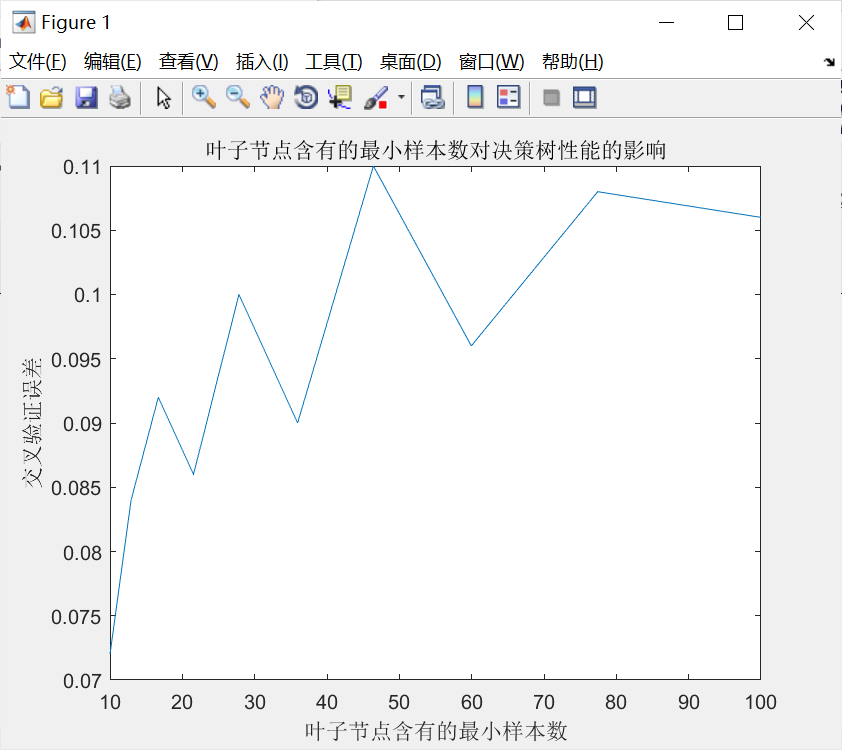
%% 叶子节点含有的最小样本数对决策树性能的影响
leafs = logspace(1,2,10);

N = numel(leafs);

err = zeros(N,1);
for n = 1:N
    t = ClassificationTree.fit(P_train,T_train,'crossval','on','minleaf',leafs(n));
    err(n) = kfoldLoss(t);
end
plot(leafs,err);
xlabel('叶子节点含有的最小样本数');
ylabel('交叉验证误差');
title('叶子节点含有的最小样本数对决策树性能的影响')

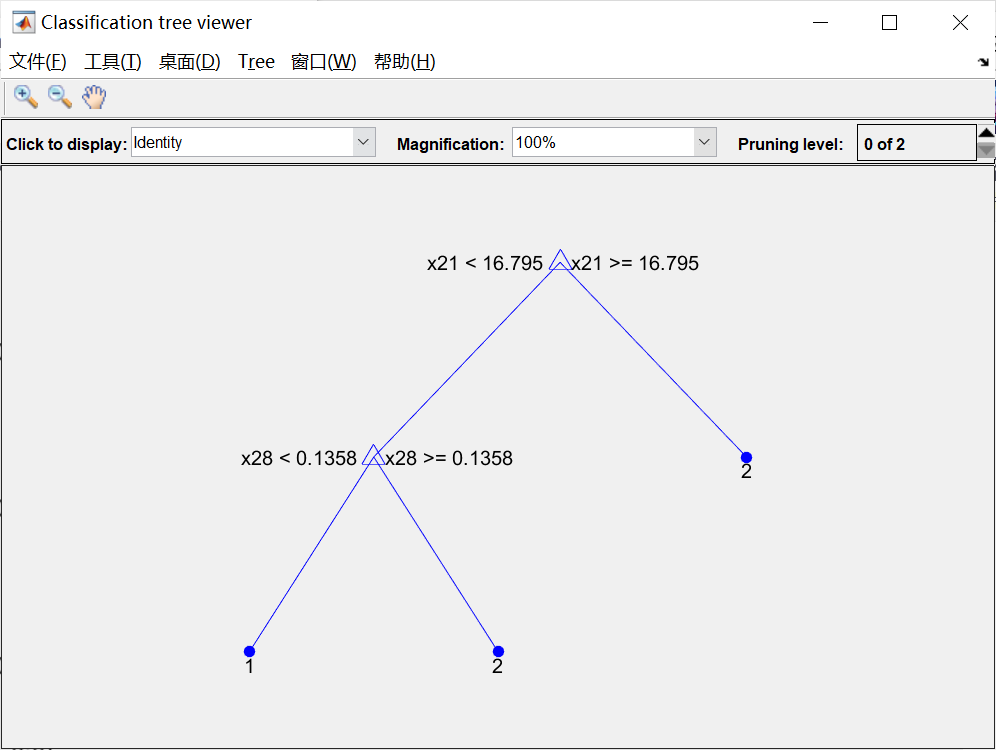
%% 设置minleaf为28，产生优化决策树
OptimalTree = ClassificationTree.fit(P_train,T_train,'minleaf',28);
view(OptimalTree,'mode','graph')

% 计算优化后决策树的重采样误差和交叉验证误差
resubOpt = resubLoss(OptimalTree)
lossOpt = kfoldLoss(crossval(OptimalTree))
% 计算优化前决策树的重采样误差和交叉验证误差
resubDefault = resubLoss(ctree)
lossDefault = kfoldLoss(crossval(ctree))

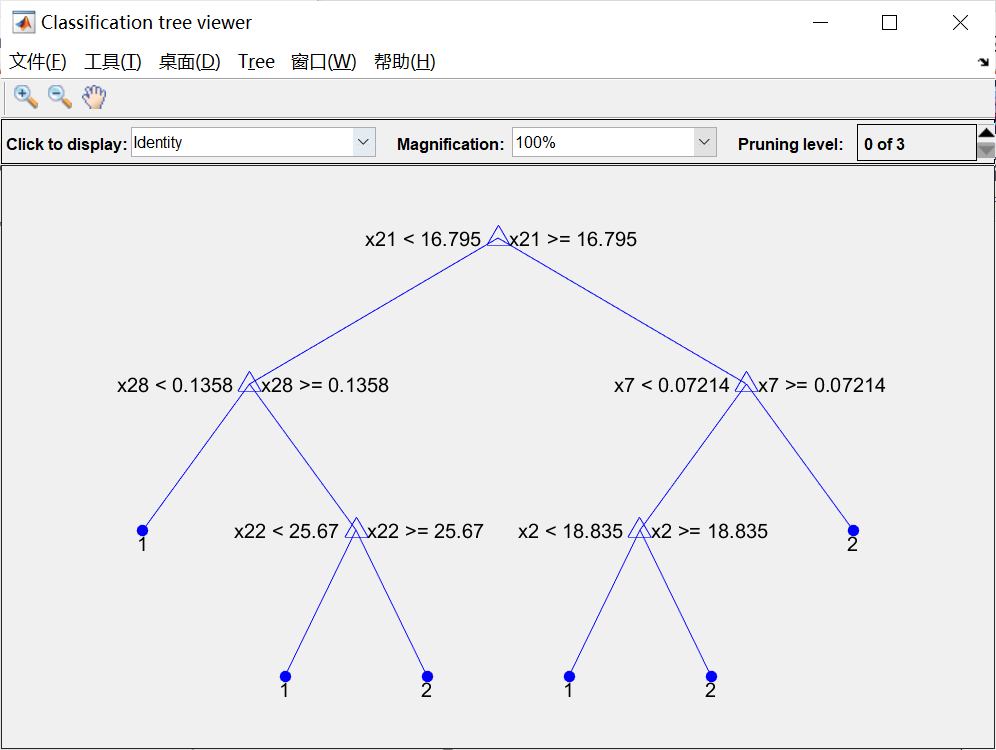
%% 剪枝
[~,~,~,bestlevel] = cvLoss(ctree,'subtrees','all','treesize','min')
cptree = prune(ctree,'Level',bestlevel);
view(cptree,'mode','graph')

% 计算剪枝后决策树的重采样误差和交叉验证误差
resubPrune = resubLoss(cptree)
lossPrune = kfoldLoss(crossval(cptree))